0. 实例图

考虑下面这样一个图

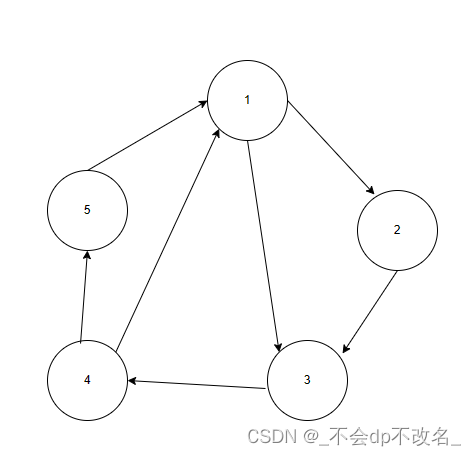
1. 邻接矩阵

vis[i][j] 表示从i 到j有一条边。直接用二维数组就可以了。

using namespace std;
int vertex_num = 5;
vector<vector<int>> graph(vertex_num, vector<int>(vertex_num, 1));

void add_edge(int u, int v){
	graph[u][v] = 1;
}
bool have_edge(int u,int v) {
	return graph[u][v];
}

对于上图，矩阵的输出就为:
$$\left(\begin{array}{ccccc}0& 1& 1& 0& 0\\ 0& 0& 1& 0& 0\\ 0& 0& 0& 1& 0\\ 1& 0& 0& 0& 1\\ 1& 0& 0& 0& 0\end{array}\right)$$

2. 邻接矩阵

对于节点i可达的点都链接在一条链上，而不是存储所有可能边，而是存实际的边。
就像是哈希表一样，链表数组。

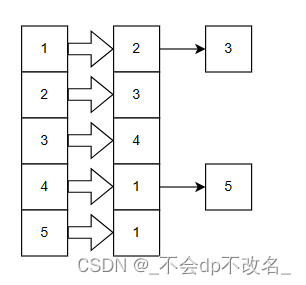
2.1 链表数组

直接用链表数组模拟，还是用vector<vector<int>>

int vertex_num = 5;
vector<vector<int>> adj(5);

void add_edge(int u,int v){
	adj[u].push_back(v);
}
bool find_edge(int u, int v) {
  for (int i = 0; i < adj[u].size(); ++i) {
    if (adj[u][i] == v) {
      return true;
    }
  }
  return false;
}

2.2 链式前向星

把所有边存在了一个数组中而已。即用两个数组模拟上面的过程。
对于以u为入点的边，我们存储时就不能存第一条以u为入点的边了，因为那样不方便插入。所以这种方式加边实际上是链表的尾插法。

我们需要存储以u为入点组成边的链表的头节点(head数组)，也就是最后插入的以u为入点的边在边数组中的下标。

注： 图中的加边顺序为边顶点坐标的字符序。

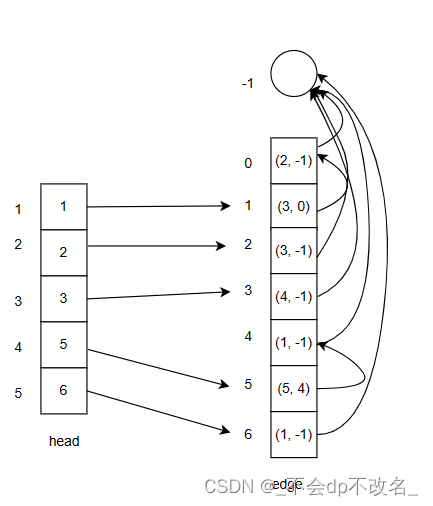
cnt = edge.size() - 1

上代码

#define MAXN 10000 + 10


struct edge {
    int to;
    int next;
    int w;
};

struct edge eg[MAXN];
int cnt = -1;
int head[MAXN];

void add_edge(int u, int v)
{
    eg[++cnt].next = head[u];
    eg[cnt].to = v;
    head[u] = cnt;
}
bool have_edge(int u, int v)
{
    for (int i = head[u]; i != -1; i = eg[i].next)
        if (eg[i].to == v)
            return true;
    
    return false;
}

memset(head, -1,sizeof(head));

3. 参考

主要内容是OIWIKI， 只是画图理解下链式前向星。