抽样是研究和数据收集中不可或缺的方法,能够从更大数据中获得有意义的见解并做出明智的决定的子集。不同的研究领域采用了不同的抽样技术,每种技术都有其独特的优点和局限性。本文将深入探讨了最常见的抽样技术,包括随机抽样、分层抽样、系统抽样、聚类抽样和便利抽样,并重点介绍了它们的应用和注意事项。

为了介绍我们先生成一些简单的数据:
import numpy as np
import matplotlib.pyplot as plt
# Create a population with known characteristics for demonstration purposes
population_size = 1000
population_mean = 50
population_std = 10
population = np.random.normal(population_mean, population_std, population_size)
随机抽样
随机抽样通常被认为是抽样技术的黄金标准。在这种方法中,总体中的每个元素都有相同的被选中的机会。随机抽样最大限度地减少了偏差,并确保样本准确地代表了总体,使其成为研究人员追求普遍性的首选。它可以通过简单的随机抽样或使用随机数生成器来实现。
sample_size = 100
random_sample = np.random.choice(population, sample_size)
分层抽样
分层抽样根据年龄、性别或收入等特定特征,将数据划分为相互排斥的子群体或阶层。在每一层内,采用随机抽样的方法选择样本。这种方法确保了每个子组的代表性,使其适用于研究人员希望在不同人口群体之间进行精确比较的情况。但是当数据没有明确划分分层时,它可能是计算密集型和具有挑战性的。
# For this example, we assume two strata - low and high income individuals
strata_low_income = population[population < 45]
strata_high_income = population[population >= 45]
sample_size_low_income = 20
sample_size_high_income = 80
stratified_sample = np.concatenate([np.random.choice(strata_low_income, sample_size_low_income), np.random.choice(strata_high_income, sample_size_high_income)])
系统抽样
系统抽样包括从总体列表中选择每n个元素。这种方法简单有效。但是如果在总体列表中存在潜在的模式,则可能导致有偏差的结果。在处理随机抽样可能不切实际的大量数据时,它特别有用。
k = population_size // sample_size # Interval
systematic_sample = population[::k]
整群抽样
整群抽样(Cluster sampling)通常根据边界将数据分成若干组(一般为地域分布)。研究人员随机选择一些群体,并从这些群体中的所有个体收集数据。该技术具有成本效益,适用于种群分布广泛的情况。如果集群不能代表整个数据,它可能会引入偏差。
# Create clusters (e.g., based on geographical regions)
cluster_size = 100
num_clusters = population_size // cluster_size
clusters = [population[i:i + cluster_size] for i in range(0, len(population), cluster_size)]
# Randomly select some individuals from the clusters
sample_cluster_sizes = [sample_size // num_clusters] * num_clusters
cluster_sample = np.concatenate([np.random.choice(cluster, size, replace=False) for cluster, size in zip(clusters, sample_cluster_sizes)])
方便抽样
便利性抽样(Convenience sampling),顾名思义就是选择那些容易接近或愿意参与的人。它是所有抽样方法中最不严格的,通常用于初步研究或在预算有限和时间有限的情况下进行调查。这可能会导致显著的偏差,因为参与者可能不能代表更广泛的人群。
# For convenience sampling, we'll randomly select individuals from the population
convenience_sample = np.random.choice(population, sample_size)
结果对比
这段代码创建了直方图来可视化得到的样本。
# Create histograms to visualize the results
plt.figure(figsize=(15, 10))
# Random Sampling Plot
plt.subplot(231)
plt.hist(random_sample, bins=20, color='b', alpha=0.7)
plt.title('Random Sampling')
# Stratified Sampling Plot
plt.subplot(232)
plt.hist(stratified_sample, bins=20, color='g', alpha=0.7)
plt.title('Stratified Sampling')
# Systematic Sampling Plot
plt.subplot(233)
plt.hist(systematic_sample, bins=20, color='r', alpha=0.7)
plt.title('Systematic Sampling')
# Cluster Sampling Plot
plt.subplot(234)
plt.hist(cluster_sample, bins=20, color='y', alpha=0.7)
plt.title('Cluster Sampling')
# Convenience Sampling Plot
plt.subplot(235)
plt.hist(convenience_sample, bins=20, color='c', alpha=0.7)
plt.title('Convenience Sampling')
plt.tight_layout()
plt.show()
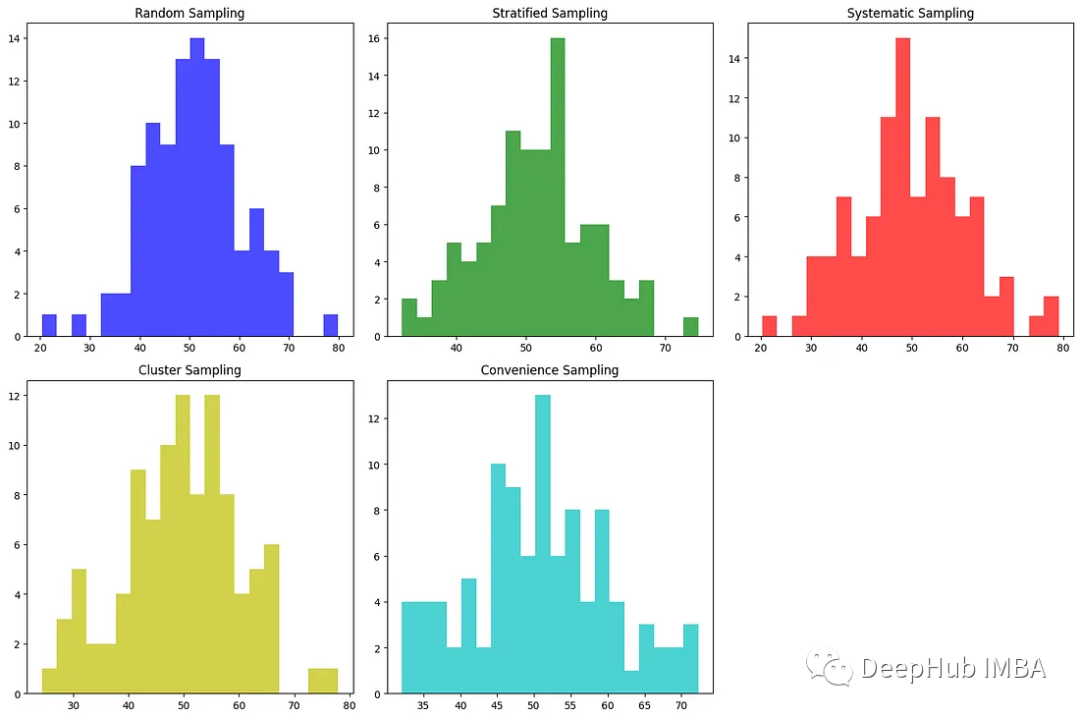
总结
抽样是研究的一个重要组成部分,它使研究人员不必检查每一个单独的因素就能得出关于数据总体的结论。每种抽样技术都有其优点和缺点,因此在选择最合适的方法之前,必须仔细考虑他们的研究目标、可用资源和数据特征。
作者:Everton Gomede
https://avoid.overfit.cn/post/d3debc422d5f4275b7d353a13a8cd7c3