模糊C均值聚类（FCM）python

news2024/11/30 0:36:45

目录

一、模糊C均值聚类的原理 

二、不使用skfuzzy的python代码

三、 使用skfuzzy的python代码

一、模糊C均值聚类的原理 

 

二、不使用skfuzzy的python代码

import numpy as np
import random
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False


'''初始化隶属矩阵'''
def initial_u0(n,K):
    '''
    :param n:样本数量
    :param K:簇的数量
    :return: 初始化的隶属矩阵
    '''
    u0=np.zeros((K,n))
    for i in range(K):
        for j in range(n):
            if i==0:
                u0[i][j]=random.uniform(0,1)
            elif i<K-1:
                s=0
                for k in range(i):
                    s=s+u0[k][j]
                u0[i][j]=random.uniform(0,1-s)
            else:
                s=0
                for k in range(i):
                    s=s+u0[k][j]
                u0[i][j]=1-s
    return u0


'''聚类函数'''
def Cluster(U,n):
    '''
    :param U:隶属度矩阵
    :param n: 样本数量
    :return: 聚类结果
    '''
    cluster=[]
    for i in range(n):
        A=U.T[i].tolist()
        a=A.index(max(A))
        cluster.append(int(a))
    return cluster


'''计算隶属中心矩阵'''
def center(data,U,m,n,K,dim):
    '''
    :param data:样本数据
    :param U: 隶属度矩阵
    :param m: 模糊加权参数，一般取2
    :param n: 样本数量
    :param K: 聚类数目
    :param dim: 维度
    :return: 隶属中心矩阵
    '''

    '''进行初始聚类'''
    cluster=Cluster(U,n)

    '''初始化隶属中心矩阵'''
    Z=np.zeros((K,dim))

    '''计算隶属中心矩阵'''
    #初始化
    u_x=[np.zeros((1,dim)) for i in range(K)]
    u=[0 for i in range(K)]
    #计算
    for i in range(n):
        c=cluster[i]  #类别
        u[c]=u[c]+(U[c][i])**m
        u_x[c]=u_x[c]+((U[c][i])**m)*data[i]
    for i in range(K):
        Z[i]=u_x[i]/u[i]

    '''返回隶属中心矩阵'''
    return Z


'''基于欧氏距离计算各点到聚类中心的距离矩阵'''
def distinct(data,n,dim,Z,K):
    '''
    :param data:样本数据
    :param n: 样本数量
    :param dim: 数据维度
    :param Z: 隶属中心矩阵
    :param K: 聚类数目
    :return: 基于欧氏距离的距离矩阵
    '''

    '''初始化距离矩阵'''
    D=np.zeros((K,n))

    '''计算欧式距离'''
    for i in range(K):
        for j in range(n):
            z=Z[i]   #隶属中心
            df=data[j]  #数据点
            df_z=df-z
            d=0
            for k in range(dim):
                d=d+(df_z[k])**2
            d=np.sqrt(d)
            D[i][j]=d

    '''返回距离矩阵'''
    return D


'''定义目标函数并返回目标函数值'''
def function(data,Z,n,dim,K,U,m,D):
    '''
    :param data:样本数据
    :param Z: 隶属中心矩阵
    :param n: 样本数量
    :param dim: 数据维度
    :param K: 聚类数目
    :param U: 隶属度矩阵
    :param m: 模糊加权参数
    :param D: 距离矩阵
    :return: 目标函数值
    '''

    '''初始化聚类'''
    cluster=Cluster(U,n)

    '''计算目标函数值'''
    J=0    #目标函数值
    W=[0 for i in range(K)]
    for i in range(n):
        c=cluster[i]  #聚类类别
        df=data[i]    #数据点
        z=Z[c]        #聚类中心
        d=D[c][i]     #数据点到聚类中心的距离
        u=U[c][i]     #隶属度
        W[c]=W[c]+(u**m)*(d**2)
    J=sum(W)

    '''返回目标函数值'''
    return J


'''更新隶属度矩阵'''
def update_U(data,Z,n,dim,K,D,m):
    '''
    :param data:样本数据
    :param Z: 隶属中心矩阵
    :param n: 样本数量
    :param dim: 数据维度
    :param K: 聚类数目
    :param D: 距离矩阵
    :param m: 模糊加权参数
    :return: 更新后的隶属度矩阵
    '''

    '''初始化隶属度矩阵'''
    U=np.zeros((K,n))

    '''更新隶属度矩阵'''
    for i in range(K):
        for j in range(n):
            r=0
            for k in range(K):
                r=r+(D[i][j]/D[k][j])**(2/(m-1))
            U[i][j]=1/r

    '''返回更新后的隶属度矩阵'''
    return U


'''模糊C均值聚类函数'''
def FCM(data,K,Tmax,m,error):
    '''
    :param data:样本数据
    :param K: 聚类数目
    :param Tmax: 最大迭代步数
    :param m: 模糊加权参数
    :param error: 迭代停止阈值，一般取0.001至0.01
    :return: 聚类结果
    '''

    '''样本数量'''
    n=data.shape[0]

    '''数据维度'''
    dim=data.shape[1]

    '''初始化隶属度矩阵'''
    U0=initial_u0(n,K)
    U=U0.copy()

    '''存储目标函数值'''
    J=[]

    '''循环'''
    for i in range(Tmax):
        #计算隶属中心矩阵
        Z=center(data,U,m,n,K,dim)
        #基于欧氏距离计算各点到聚类中心的距离矩阵
        D=distinct(data,n,dim,Z,K)
        #计算目标函数的值
        J.append(function(data,Z,n,dim,K,U,m,D))
        #更新隶属度矩阵
        U=update_U(data,Z,n,dim,K,D,m)
        #判断阈值
        if i!=0 and abs(J[i-1]-J[i])<=error:
            break

    '''得到聚类结果'''
    cluster=Cluster(U,n)

    '''返回聚类结果(聚类类别，聚类中心，目标函数值）'''
    return cluster,Z,J[-1]


'''主函数'''
if __name__=="__main__":

    '''随机产生400组在区间[0,1]上的二维数据'''
    data=np.array([[random.uniform(0, 1) for i in range(2)] for j in range(400)])

    '''聚类'''
    cluster,cntr,J=FCM(data,K=4,Tmax=1000,m=2,error=0.0001)

    print("聚类结果：\n{}".format(cluster))
    print("目标函数值：\n{}".format(J))


    #将数据分类
    fdata=data.tolist()
    X1=[]
    Y1=[]
    X2=[]
    Y2=[]
    X3=[]
    Y3=[]
    X4=[]
    Y4=[]
    for i in range(400):
        if cluster[i]==0:
            X1.append(fdata[i][0])
            Y1.append(fdata[i][1])
        if cluster[i]==1:
            X2.append(fdata[i][0])
            Y2.append(fdata[i][1])
        if cluster[i]==2:
            X3.append(fdata[i][0])
            Y3.append(fdata[i][1])
        if cluster[i]==3:
            X4.append(fdata[i][0])
            Y4.append(fdata[i][1])

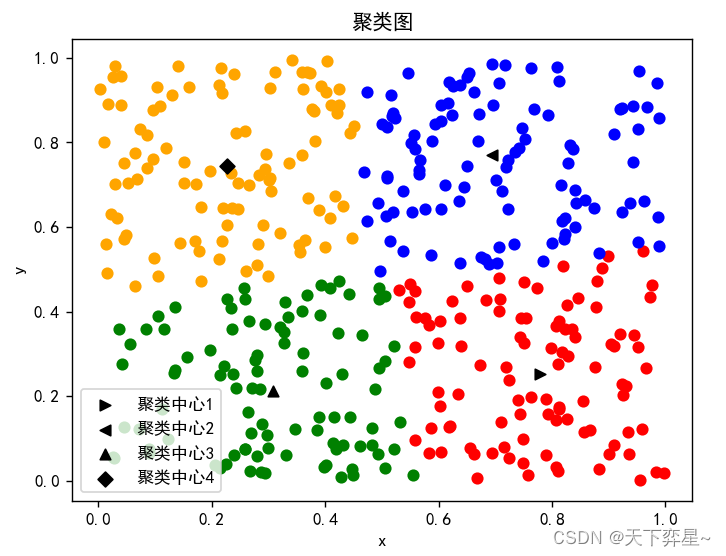
    # 聚类图
    plt.scatter(X1, Y1, c='red', marker='o')
    plt.scatter([cntr[0][0]], [cntr[0][1]], marker='>', c="black", label='聚类中心1')
    plt.scatter(X2, Y2, c='blue', marker="o")
    plt.scatter([cntr[1][0]], [cntr[1][1]], marker='<', c="black", label="聚类中心2")
    plt.scatter(X3, Y3, c='green', marker="o")
    plt.scatter([cntr[2][0]], [cntr[2][1]], marker='^', c="black", label="聚类中心3")
    plt.scatter(X4, Y4, c='orange', marker="o")
    plt.scatter([cntr[3][0]], [cntr[3][1]], marker="D", c="black", label="聚类中心4")
    plt.legend()
    plt.xlabel("x")
    plt.ylabel("y")
    plt.title("聚类图")
    plt.show()

三、 使用skfuzzy的python代码

import numpy as np
import random
import skfuzzy as fuzz
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False


'''随机产生400组在区间[0,1]上的二维数据'''
data = np.array([[random.uniform(0,1) for i in range(2)] for j in range(400)])


'''初始化隶属度矩阵（聚成4类）'''
'''
cntr：聚类中心
u：最后的隶属度矩阵
u0：初始化的隶属度矩阵
d：是一个矩阵，记录每一个点到聚类中心的欧式距离
jm：是目标函数的优化历史
p：p是迭代的次数
fpc：全称是fuzzy partition coefficient， 是一个评价分类好坏的指标，它的范围是0到1, 1表示效果最好，后面可以通过它来选择聚类的个数。
'''
cntr, u, u0, d, jm, p, fpc = fuzz.cluster.cmeans(data.T, 4, 2, error=0.0001, maxiter=1000)


'''迭代计算'''
cntr, u, u0, d, jm, p, fpc = fuzz.cluster.cmeans(data.T, 4,2, error=0.0001, maxiter=1000)


'''获得聚类结果'''
cluster_membership = np.argmax(u, axis=0)


'''绘制聚类结果'''
#将数据分类
fdata=data.tolist()
X1=[]
Y1=[]
X2=[]
Y2=[]
X3=[]
Y3=[]
X4=[]
Y4=[]
for i in range(400):
    if cluster_membership[i]==0:
        X1.append(fdata[i][0])
        Y1.append(fdata[i][1])
    if cluster_membership[i]==1:
        X2.append(fdata[i][0])
        Y2.append(fdata[i][1])
    if cluster_membership[i]==2:
        X3.append(fdata[i][0])
        Y3.append(fdata[i][1])
    if cluster_membership[i]==3:
        X4.append(fdata[i][0])
        Y4.append(fdata[i][1])

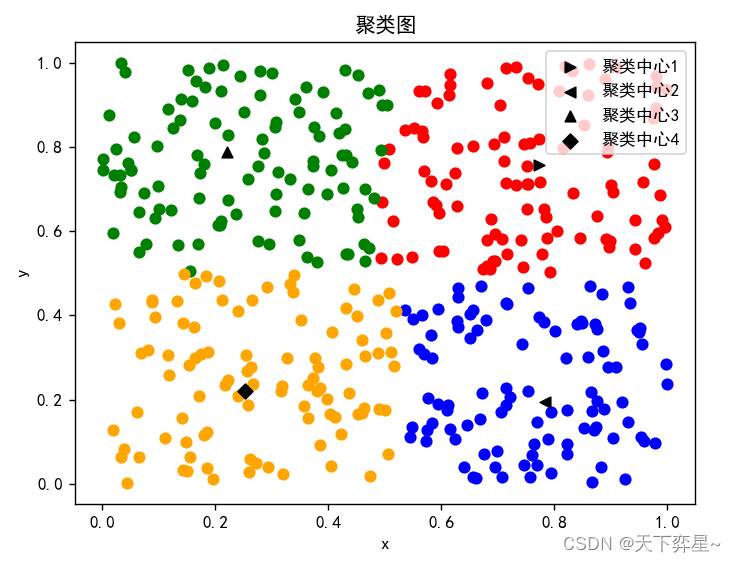
#聚类图
plt.scatter(X1,Y1,c='red',marker='o')
plt.scatter([cntr[0][0]],[cntr[0][1]],marker='>',c="black",label='聚类中心1')
plt.scatter(X2,Y2,c='blue',marker="o")
plt.scatter([cntr[1][0]],[cntr[1][1]],marker='<',c="black",label="聚类中心2")
plt.scatter(X3,Y3,c='green',marker="o")
plt.scatter([cntr[2][0]],[cntr[2][1]],marker='^',c="black",label="聚类中心3")
plt.scatter(X4,Y4,c='orange',marker="o")
plt.scatter([cntr[3][0]],[cntr[3][1]],marker="D",c="black",label="聚类中心4")
plt.legend()
plt.xlabel("x")
plt.ylabel("y")
plt.title("聚类图")
plt.show()

print(cluster_membership)
'''
print("cntr:\n{}".format(cntr))
print("u:\n{}".format(u))
print("u0:\n{}".format(u0))
print("d:\n{}".format(d))
print("jm:\n{}".format(jm))
print("p:\n{}".format(p))
print("fpc:\n{}".format(fpc))
'''

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1159691.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

记录 vue + vuetify + electron 安装过程

记录 vue + vuetify + electron 安装过程

NodeJs 版本&#xff1a; 20 内容来自&#xff1a; Electron Vue.js Vuetify 构建跨平台应用_思月行云的博客-CSDN博客文章浏览阅读61次。Go coding!https://blog.csdn.net/kenkao/article/details/132600542 npm config set registry https://registry.npm.taobao.org np…
阅读更多...
Physics2DPlugin3加载后会跳转gsap官网解决

Physics2DPlugin3加载后会跳转gsap官网解决

因工作需要使用Physics2DPlugin3库&#xff0c;目标效果 加载他里面的在线js&#xff0c;使用效果正常&#xff0c;但是几秒会跳转官网&#xff0c;我们app内部、浏览器都会这样。 于是研究js代码&#xff0c;发现里面有setTimeout跳转。 删掉就好了 分享我改好的文件&#x…
阅读更多...
uniapp原生插件之安卓获取设备唯一标识

uniapp原生插件之安卓获取设备唯一标识

插件介绍 安卓获取设备唯一标识&#xff0c;集成了获取imei&#xff0c;获取安卓ID&#xff0c;获取GUID&#xff0c;获取获取OAID/AAID等 插件地址 安卓获取设备唯一标识 - DCloud 插件市场 超级福利 uniapp 插件购买超级福利 详细使用文档 uniapp 安卓获取设备唯一标…
阅读更多...
Unity 粒子特效-第五集-烟雾缭绕合并特效

Unity 粒子特效-第五集-烟雾缭绕合并特效

一、特效预览 二、制作原理 1.素材介绍 我们之前几章做了有光球&#xff0c;星星&#xff0c;烟雾 我们把他们结合起来&#xff0c;做一些调整 2.合并方法 我们还是建一个粒子游戏物体 我们把所有的效果取消 再重置一下transform 现在这个物体就是一个可以控制粒子特效的空…
阅读更多...
BUUCTF webshell后门 1

BUUCTF webshell后门 1

BUUCTF:https://buuoj.cn/challenges 题目描述&#xff1a; 朋友的网站被黑客上传了webshell后门&#xff0c;他把网站打包备份了&#xff0c;你能帮忙找到黑客的webshell在哪吗&#xff1f;(Webshell中的密码(md5)即为答案) 密文&#xff1a; 下载附件&#xff0c;解压得到一…
阅读更多...
Test-Agent----基于Centos7系统部署Test-Agent

Test-Agent----基于Centos7系统部署Test-Agent

【Test-Agent----基于Centos7系统部署Test-Agent】 一、部署 Test-Agent 1.1 环境准备 环境基本信息&#xff1a;Centos7.9操作系统&#xff0c;16核64G1T硬盘&#xff0c;Python3.9.7 1.2 部署 Test-Agent &#xff08;1&#xff09;安装git-lfs cd /opt curl -s https:…
阅读更多...
git生成gitee和github两个不同的公钥

git生成gitee和github两个不同的公钥

配置多个公钥 Windows 用户建议使用 Windows PowerShell 或者 Git Bash&#xff0c;在 命令提示符 下无 cat 和 ls 命令。 1、生成公钥文件&#xff1a; 通过命令 ssh-keygen 生成 SSH Key&#xff1a; ssh-keygen -t rsa -C "Gitee SSH Key" -f ~/.ssh/gitee_be…
阅读更多...
端到端Scrum敏捷管理流程-

端到端Scrum敏捷管理流程-

Leangoo领歌是一款永久免费的专业的敏捷开发管理工具&#xff0c;提供端到端敏捷研发管理解决方案&#xff0c;涵盖敏捷需求管理、任务协同、进展跟踪、统计度量等。 Leangoo领歌上手快、实施成本低&#xff0c;可帮助企业快速落地敏捷&#xff0c;提质增效、缩短周期、加速创新…
阅读更多...
大麦协议开发

大麦协议开发

1. 用户抢购请求处理&#xff1a; - 后端实现&#xff1a;在后端&#xff0c;您可以创建一个用于处理用户抢购请求的接口。当用户发起抢购请求时&#xff0c;后端会根据一定的算法和逻辑来处理请求。例如&#xff0c;可以使用分布式锁来保证只有一个用户能够成功抢购。示例后端…
阅读更多...
uniapp实现路线规划

uniapp实现路线规划

UniApp是一个基于Vue.js框架开发的跨平台应用开发框架&#xff0c;可以同时构建iOS、Android、H5等多个平台的应用。它使用了基于前端技术栈的Web开发方式&#xff0c;通过编写一套代码&#xff0c;即可在不同平台上运行和发布应用。 UniApp具有以下特点&#xff1a; 跨平台开…
阅读更多...
Python画图之樱花树

Python画图之樱花树

Python-turtle画出樱花树&#xff08;有趣小游戏&#xff09; 一、效果图二、Python代码 一、效果图 二、Python代码 #!/usr/bin/env python # codingutf-8 # 画一棵樱花import turtle as T import random from time import sleep# 画樱花的躯干(60,t) def tree(branchLen,t):…
阅读更多...
应用性能管理：用户的使用体验应该如何监控？

应用性能管理：用户的使用体验应该如何监控？

目录 前言 一、什么是应用用性能管理 二、如何搭建 APM 系统 三、什么是Skywalking 一、Skywalking原理数据库 二、为什么Skywalking侵入性小 三、Skywalking Agent原理 四、Skywalking登录地址 五、Skyworking oap原理 六、Skywalking mysql 七、Skywalking版本选取 …
阅读更多...
C语言 每日一题 Day10

C语言 每日一题 Day10

1.使用函数判断完全平方数 本题要求实现一个判断整数是否为完全平方数的简单函数。 函数接口定义&#xff1a; int IsSquare(int n); 其中n是用户传入的参数&#xff0c;在长整型范围内。如果n是完全平方数&#xff0c;则函数IsSquare必须返回1&#xff0c;否则返回0。 代码实…
阅读更多...
软考之软件工程基础理论知识

软考之软件工程基础理论知识

软件工程基础 软件开发方法 结构化方法 将整个系统的开发过程分为若干阶段&#xff0c;然后依次进行&#xff0c;前一阶段是后一阶段的工作依据按顺序完成。应用最广泛。特点是注重开发过程的整体性和全局性。缺点是开发周期长文档设计说明繁琐&#xff0c;工作效率低开发前要…
阅读更多...
python脚本监听域名证书过期时间，并将通知消息到钉钉

python脚本监听域名证书过期时间，并将通知消息到钉钉

版本一&#xff1a; 执行脚本带上 --dingtalk-webhook和–domains后指定钉钉token和域名 python3 ssl_spirtime.py --dingtalk-webhook https://oapi.dingtalk.com/robot/send?access_tokenavd345324 --domains www.abc1.com www.abc2.com www.abc3.com脚本如下 #!/usr/bin…
阅读更多...
pytorch笔记 GRUCELL

pytorch笔记 GRUCELL

1 介绍 GRU的一个单元 2 基本使用方法 torch.nn.GRUCell(input_size, hidden_size, biasTrue, deviceNone, dtypeNone) 输入&#xff1a;&#xff08;batch&#xff0c;input_size&#xff09; 输出和隐藏层&#xff1a;&#xff08;batch&#xff0c;hidden_size&#xf…
阅读更多...
Unity 报警告warning CS0649: Field ‘...‘ is never assigned to,...解决办法

Unity 报警告warning CS0649: Field ‘...‘ is never assigned to,...解决办法

文章目录 1. 现象2. 警告出现原因3. 解决方法 1. 现象 2. 警告出现原因 该警告应仅出现在私有成员变量中。那些不能从外部设置&#xff0c;这就是为什么编译器可以确定这些变量没有在任何地方蛇者其值。在C&#xff03;中&#xff0c;没有访问修饰符的变量&#xff08;private…
阅读更多...
React中的状态管理

React中的状态管理

目录 前言 1. React中的状态管理 1.1 本地状态管理 1.2 全局状态管理 Redux React Context 2. React状态管理的优势 总结 前言 当谈到前端开发中的状态管理时&#xff0c;React是一个备受推崇的选择。React的状态管理机制被广泛应用于构建大型、复杂的应用程序&#xf…
阅读更多...
2023.04.08春天来了，各种各样的花开了

2023.04.08春天来了，各种各样的花开了

阅读更多...
HNU-编译原理-讨论课1

HNU-编译原理-讨论课1

讨论课安排&#xff1a;2次4学时&#xff0c;分别完成四大主题讨论 分组&#xff1a;每个班分为8组&#xff0c;每组4~5人&#xff0c;自选组长1人 要求和说明&#xff1a; 以小组为单位上台报告&#xff1b;每次每组汇报2个小主题&#xff0c;每组按要求在2个小主题中各选1…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023