Portal.

悬线法。

悬线法，主要用来解决最大子矩形问题，由王知昆在 IOI2003 国家集训队论文中提出。

所谓“最大子矩形问题”，就是在一个给定的矩形网格中有一些障碍点，要找出网格内部不包含任何障碍点，且边界与坐标轴平行的最大矩形。

所谓悬线，就是对于一类线段，除了两个端点之外，不覆盖任何障碍点，我们称它为有效线段；上端点覆盖了一个障碍点或达到整个矩形上端的有效线段，就是悬线，相当于宽为 $0$ 的矩形。

举个例子，下面这几条线，都是悬线：

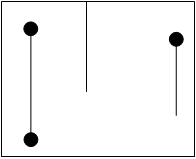
所谓悬线法，就是先找出每一个点对应的悬线的长度，然后左右移动找到对应的最大宽度。

用一张图来看一下，会发现每一个极大矩形都可以由悬线扩展而来：

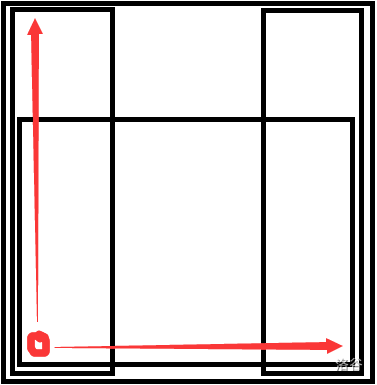
定义：

• $\text{left}(i,j)$ 表示底部为 $(i,j)$ 的悬线能到达的最左位置。
• $\text{right}(i,j)$ 表示底部为 $(i,j)$ 的悬线能到达的最右位置。
• $\text{height}(i,j)$ 表示从 $(i,j)$ 能向上扩展的最大高度。

初始化：
$$\begin{array}{rl}& \text{height}(i,j)=1\\ & \text{left}(i,j)=0\\ & \text{right}(i,j)=m\end{array}$$
状态转移方程：
$$\begin{array}{rl}& \text{height}(i,j)=\text{height}(i-1,j)+1\\ & \text{left}(i,j)=\max (\text{left}(i-1,j),\text{left}(i,j))\\ & \text{right}(i,j)=\min (\text{right}(i-1,j),\text{right}(i,j))\end{array}$$
可以在 $O(1)$ 的时间复杂度内完成对每条悬线的操作。

对于这道题来说，以长方形、正方形讨论即可。题目要求 $01$ 交错，所以只需要相邻的点不相等即可。

代码如下：

#include <bits/stdc++.h>
using namespace std;

const int maxn=2005;
int gg[maxn][maxn],leftt[maxn][maxn]/*万能头里有left函数*/,rightt[maxn][maxn],height[maxn][maxn],N,M,ans1,ans2;

int main()
{
	cin>>N>>M;
	for(int i=1;i<=N;i++)
		for(int j=1;j<=M;j++)
		{
			cin>>gg[i][j];
			leftt[i][j]=rightt[i][j]=j;//建立悬线
			height[i][j]=1;//初始化，如果上下两个点相同也可以有一条长度为1的悬线
		}
	for(int i=1;i<=N;i++)
		for(int j=2;j<=M;j++)//注意从2开始
			if(gg[i][j]!=gg[i][j-1])
				leftt[i][j]=leftt[i][j-1];//预处理左边界
	for(int i=1;i<=N;i++)
		for(int j=M-1;j>0;j--)//注意从M-1开始
			if(gg[i][j]!=gg[i][j+1])
				rightt[i][j]=rightt[i][j+1];//预处理右边界，注意要从终边开始减
	for(int i=1;i<=N;i++)
		for(int j=1;j<=M;j++)
		{
			if(i>1&&gg[i][j]!=gg[i-1][j])
			{
				leftt[i][j]=max(leftt[i][j],leftt[i-1][j]);
				rightt[i][j]=min(rightt[i][j],rightt[i-1][j]);
				height[i][j]=height[i-1][j]+1;
			}
			int a=rightt[i][j]-leftt[i][j]+1/*横向长度*/,b=min(a,height[i][j]);
			ans1=max(ans1,b*b);ans2=max(ans2,a*height[i][j]);
		}
	cout<<ans1<<endl<<ans2;
	return 0;
}