目录

引入

代码实现

复杂度分析

---

引入

类比树的广度优先遍历（层序遍历），通过一个队列不断地实现出队的同时把左右孩子入队的操作实现广度优先遍历，值得注意的是图是否有环的情况。

 

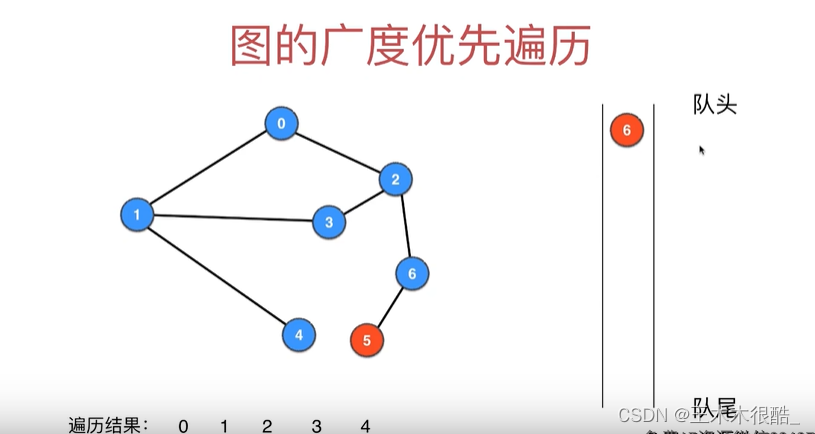
用相似的方法可以实现图的广度优先遍历，每个顶点一入队就会被标记成visited，有了标记的顶点下次被访问时就不用入队了。 

代码实现

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;

public class GraphBFS {

    private Graph G;
    private boolean[] visited;

    private ArrayList<Integer> order = new ArrayList<>();//存储遍历的顺序

    public GraphBFS(Graph G){

        this.G = G;
        visited = new boolean[G.V()];//我们图中有多少个顶点，visited就有多少个空间
        for(int v = 0; v < G.V(); v ++)
            if(!visited[v])//保证把所有顶点遍历完
                bfs(v);
    }

    private void bfs(int s){

        Queue<Integer> queue = new LinkedList<>();//queue不是一个类，是一个接口
        queue.add(s);//从某个顶点出发，入队
        visited[s] = true;
        while(!queue.isEmpty()){
            int v = queue.remove();
            order.add(v);

            for(int w: G.adj(v))//查看v这个顶点所有的相邻顶点
                if(!visited[w]){
                    queue.add(w);
                    visited[w] = true;//每个顶点只会入队一次、出队一次
                }
        }
    }

    public Iterable<Integer> order(){
        return order;
    }

    public static void main(String[] args){

        Graph g = new Graph("g.txt");//从文件中读取图的信息
        GraphBFS graphBFS = new GraphBFS(g);//类的对象
        System.out.println("BFS Order : " + graphBFS.order());
    }
}

复杂度分析

所有的顶点都遍历了一遍，每次取出一个顶点都会遍历一下它的邻边，所以它的时间复杂度是