目录
一、图着色问题
1、算法设计
2、代码
二、旅行商问题
1、概述问题
2、穷举法
3、回溯法
一、图着色问题
1、算法设计
图着色问题,给定图中各个区域的相邻关系,抽象成一个无向图G=(V,E),给定m种颜色,可以选择一个颜色可以对每一个区域(无向图的顶点)进行着色,但需要保证相邻区域之间不能颜色相同,如下图的无向图表示。
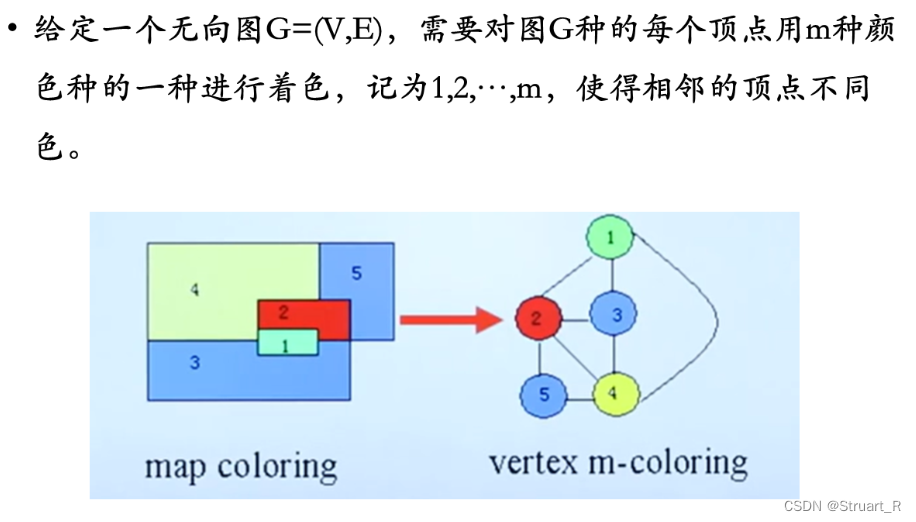
无向图采用建立邻接矩阵a[ ][ ]来表示。注意:i和j都是从1开始的,而不是0开始的,所以邻接矩阵的0行0列,设定为-1,表示不存在。
算法:回溯法,子集树方法。
backtrack回溯过程:
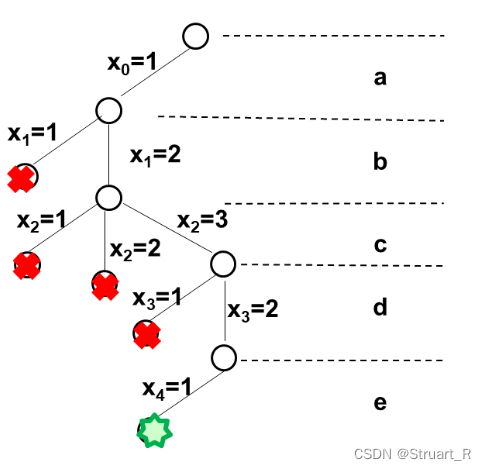
(1)首先判断是否叶子结点已经搜索,即t>n,若满足条件,则输出当前着色方法,sum++。
(2)若不满足条件,则在当前层遍历m种颜色,若该颜色满足扩展条件,则扩展该叶子结点搜索下一层,否则选择下一个颜色,直到所有颜色都不满足条件则回溯上一层。
(3)扩展条件:遍历n个结点,若结点与叶子结点有相邻关系a[t][i]==1且叶子结点和该遍历的结点颜色相同x[t]==x[i],则返回false,否则存在一个结点有相邻关系且颜色不同,返回true用来做新的扩展结点。
(4)另外,判断(t<=n)&&x[t]==m,如果当前层数不在叶子结点层(第n层),且该层修改的颜色值为最后一个颜色(由于颜色按顺序遍历),则颜色置0,退出当前迭代层,返回上一层。也就是说当前叶子结点的所有子树都搜索过了,该结点变为死结点,要么返回到该叶子结点的邻树,要么返回叶结点上一层。
2、代码
//图着色问题
public class graphcoloration {
static int n=5; //顶点数
static int m=3; //颜色数
static int a[][]={ //邻接矩阵
{-1,-1,-1,-1,-1,-1},
{-1,0,1,1,1,0},
{-1,1,0,1,0,1},
{-1,1,1,0,1,1},
{-1,1,0,1,0,1},
{-1,0,1,1,1,0}
}; //-1是不存在0点,0是不可达
static int sum=0; //可行解
public static void main(String[] args)
{
int x[]=new int[n+1]; //x存储可达的路线
backtrack(1, x); //初始节点在第一层
System.out.println(sum); //输出有多少种可行解
}
public static void backtrack(int t,int x[])
{
if(t>n)
{
sum++;
for(int i=1;i<=n;i++)
{
System.out.print(x[i]+" ");
}
System.out.println();
}
else{
for(int i=1;i<=m;i++)
{
x[t]=i;
if(OK(t,x)) //如果满足扩展条件则扩展
backtrack(t+1, x);
if((t<=n)&&x[t]==m) //如果当前层数不在叶子结点,且该层修改的数为最后一个颜色,则颜色置0,退出当前迭代层
{
x[t]=0;
break;
}
}
}
}
public static boolean OK(int t,int x[])
{
for(int i=1;i<=n;i++)
{
if((a[t][i]==1)&&x[t]==x[i]) //判断所有相邻关系中颜色相同的返回false
return false;
}
return true; //留下的都是存在相邻关系且颜色不同的返回true
}
}
二、旅行商问题
1、概述问题
一个旅行商希望从一个城市出发访问n个城市,每个城市只能访问一次,且开始和结束在同一城市,给出一个不同城市之间距离的加权完全图,请设计一个算法,找到旅行商的最短路径。也就是图论中的求出最小的哈密顿回路。
下面的算法依照下图为例,出发为a点。
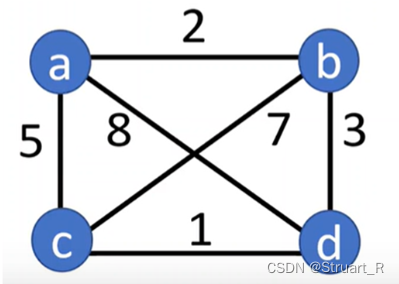
2、穷举法
穷举法就是求所有a为出发点,a为终点的全排列。
全排列算法:
(1)全排列算法使用递归算法,如果迭代到最后一层,则计算当前路线的加权和(注意第一个值不用进行全排列,因为初始点不动),minl存放加权和最小的值。
(2)若没有迭代到最后一层,则遍历k<=i<=n,k为当前全排列迭代的层数,交换op[i]和op[k],继续排列k+1层,再交换op[i]和op[k],保证对后续没有影响。
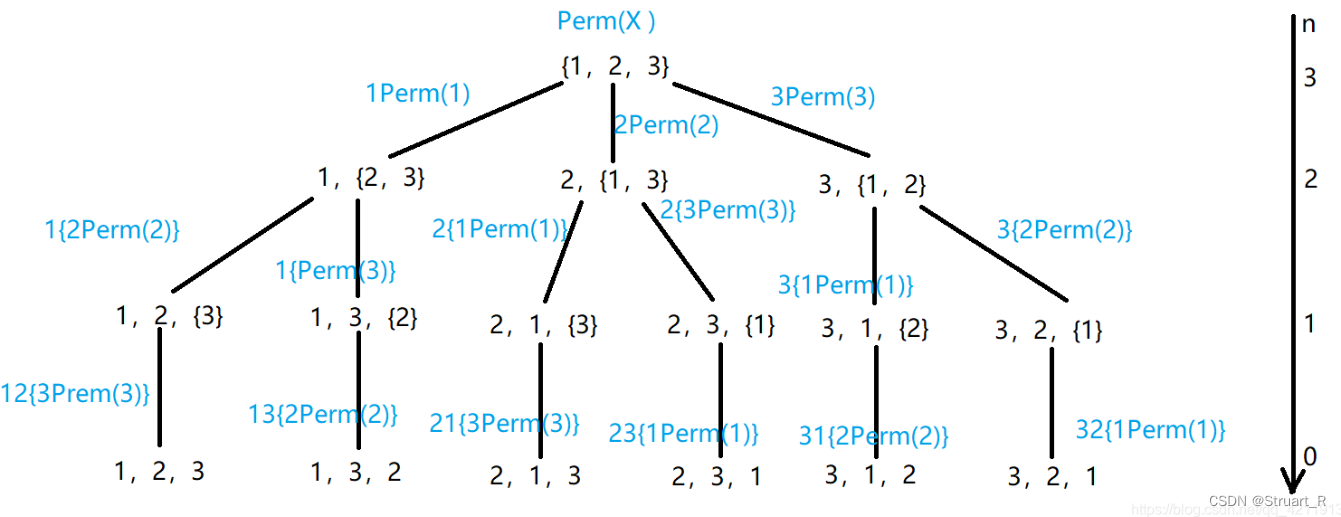
代码如下:
//旅行商问题
public class tsp {
public static final int MAX=9999;
public static int[][] a={
{MAX,MAX,MAX,MAX,MAX},
{MAX,MAX,2,5,8},
{MAX,2,MAX,7,3},
{MAX,5,7,MAX,1},
{MAX,8,3,1,MAX},
};
public static int n=4;
public static int minl=999;
public static void main(String []args)
{
int op[]=new int[n+1];
for(int i=1;i<=n;i++)
op[i]=i;
perm(2,op);
System.out.println(minl);
}
//全排列算法
public static void perm(int k,int op[])
{
if(k==n)
{
int tmp=calulate(op);
minl=tmp<minl?tmp:minl;
}
for(int i=k;i<=n;i++)
{
swap(i,k,op);
perm(k+1,op);
swap(i,k,op);
}
}
//交换数组中元素
public static void swap(int i,int k,int []op)
{
int tmp=op[i];
op[i]=op[k];
op[k]=tmp;
}
//计算全排列后当前排列的加权和
public static int calulate(int []op)
{
int tot=0;
for(int i=1;i<n;i++)
{
tot+=a[op[i]][op[i+1]];
}
tot+=a[op[n]][1];
return tot;
}
}
3、回溯法
时间复杂度分析:对于回溯法(本质上也是穷举法)和穷举法的时间复杂度都是O(n!),所以随着城市的数量增加,计算时间指数级增长,所以对于大规模的TSP问题可以采用动态规划、启发式算法等方法,来在短时间接近最优解,但这一定不是完备的。
算法流程:
(1)首先判断是否叶子结点已经搜索,即满足k>n,则计算当前加权和,minl保存最小的加权和。
(2)若不满足,则遍历所有叶子结点,是否存在可以扩展的结点,进行扩展迭代到下一层,若没有则返回上一层。
(3)扩展条件:判断所有结点中满足a[k][i]!=MAX即待扩展节点与判断结点不可达,且x[k]==x[i]待扩展节点与判断结点相同,则不可扩展。也就是存在某一节点可以到达,且与上一个结点不同,则扩展。
//旅行商问题
public class tsp {
public static final int MAX=9999;
public static int[][] a={
{MAX,MAX,MAX,MAX,MAX},
{MAX,MAX,2,5,8},
{MAX,2,MAX,7,3},
{MAX,5,7,MAX,1},
{MAX,8,3,1,MAX},
};
public static int n=4;
public static int minl=999;
public static void main(String []args)
{
int op[]=new int[n+1];
int x[]=new int[n+1];
for(int i=1;i<=n;i++)
op[i]=i;
backtrack(1,x);
System.out.println(minl);
}
//回溯法
public static void backtrack(int k,int x[])
{
//注意这里一定要大于号,也就是已经判断好当前路径的叶子结点,再进行输出,或者替换最小值。
if(k>n)
{
int tot=0;
for(int i=1;i<n;i++)
tot+=a[x[i]][x[i+1]];
tot+=a[x[n]][x[1]];
minl=minl<tot?minl:tot;
}
else
{
for(int i=1;i<=n;i++)
{
x[k]=i;
if(Ok(k, x))
backtrack(k+1,x);
}
}
}
//判断是否能继续扩展
public static boolean Ok(int k,int x[])
{
for(int i=1;i<=n;i++)
{
if(a[k][i]!=MAX&&x[k]==x[i])
return false;
}
return true;
}
}