轻松理解 Transformers（2）：Attention部分

编者按：随着人工智能技术的不断发展，Transformers 模型架构已成为自然语言处理领域的重要基石。然而，许多人对其内部工作机制仍然感到困惑。本文通过浅显易懂的语言和生活中的例子，帮助读者逐步理解 Transformers 中最核心的 Attention 机制。

本文是Transformers系列的第二篇。作者的核心观点是：Attention 机制是 Transformers 模型区分关键信息的关键所在。本文通过直观的类比和数学公式，让读者对 Attention 的计算过程有更深入的理解。文章详细介绍了Attention 机制如何辨别不同单词的重要性；Query、Key、Value 矩阵及其在 Attention 计算过程中的作用；Masking 如何屏蔽无关内容；Dropout、Skip Connection 等机制如何提升模型稳定性；Add & Norm 层的工作原理，以及归一化对模型学习的重要性。

虽然 Transformers 中各个组件之间相互关联，难以一口气理解全貌，但本文通过耐心讲解 Attention 这一核心机制，确实让读者对整体架构有了更扎实的把握。我们衷心希望这类通俗易懂的文章能帮助更多读者了解 Transformers 技术的运行原理。

以下是译文，enjoy！

作者 | Chen Margalit

编译 | 岳扬

本文经原作者授权，由Baihai IDP编译。如需转载译文，请联系获取授权。

原文链接：https://towardsdatascience.com/transformers-part-3-attention-7b95881714df

🚢🚢🚢欢迎小伙伴们加入AI技术软件及技术交流群，追踪前沿热点，共探技术难题~

Transformers 对人工智能领域，乃至对整个世界都产生了深远的影响。这种模型架构由多个组件构成，但正如提出该架构那篇论文的题目——Attention is All You Need，显然注意力机制（Attention）具有特别重要的意义。本系列的第二部分将主要关注注意力（Attention）及其相关功能，这些功能确保了 Transformer 各组件的良好配合。

图片来自 Vaswani, A. 等人的论文[1]

01 注意力机制（Attention）

在 Transformers 中， attention 指的是一种机制，它能让模型在处理过程中专注于输入（input）的相关部分。可以将其想象成一把手电筒，照亮句子的特定部分，并根据语境（context）判断其在句子中的重要程度。 我认为举几个例子比直接将定义摆出来更有效，通过提供具体的例子，可以激发大脑的思考和理解能力，使大脑有机会自己去理解概念，而不仅仅依赖于定义。

当看到句子“The man took the chair and disappeared”时，我们自然而然地会对句子的不同部分赋予不同程度的重要性（即注意力（attention））。但令我惊讶的是，如果我们去掉一些特定的词，句子的意思基本保持不变：“man took chair disappeared”。虽然这个版本的英语句子有些不通顺，但与原句相比，我们仍然可以理解这句话要表达信息的本质。有趣的是，三个单词（“The”、"the "和 “and”）占据了句子中词数的43%，但对句子的整体意思没有太大影响。在柏林生活期间，我的德语说得非常棒，每一个接触过我的柏林人可能都这么认为（要么学好德语，要么快乐，这是我必须做出的决定），但对于机器学习模型来说，这一点就不那么明显了。

过去，像循环神经网络（RNNs）等早期架构面临着一个重大挑战：它们难以“记住”输入序列（长度通常超过20个单词）中较远位置的单词。众所周知，这些模型主要依靠数学运算来处理数据。不幸的是，这些早期模型架构中使用的数学运算不够高效，无法将单词表征传递到序列的较远位置。

这种长程依赖（long-term dependency）的限制阻碍了循环神经网络（RNN）长时间保持上下文信息的能力，从而影响了语言翻译或情感分析等任务，因为在这些任务中，理解整个输入序列至关重要。然而，Transformer 通过其注意力机制和自注意力机制更有效地解决了这个问题。 它们可以高效地捕捉输入中的长距离依赖关系，使模型能够保留语境和关联信息，即使是序列中更早出现的单词也不例外。因此，Transformer 已成为克服以往架构限制的开创性解决方案，并明显提高了各种自然语言处理任务的性能。

要创造出像我们今天所遇到的高级聊天机器人这样的优秀产品，就必须让模型具备区分高价值和低价值单词的能力，并在输入的中长距离保留上下文信息。Transformer架构为应对这些挑战而引入的机制被称为注意力机制。

02 点积 Dot Product

神经网络模型如何在理论上辨别不同单词的重要性呢？在分析句子时，我们的目标是找出相互之间关系更紧密的词语。 由于这些单词已经被表示为向量（由数字组成），因此我们需要一种测量数字之间相似性的方法。测量向量之间相似性的数学术语是“点积”（Dot Product）。它涉及将两个向量的元素相乘，并产生一个标量值（例如2、16、-4.43），该值能够表示这两个向量的相似性。机器学习建立在各种数学运算的基础上，其中点积尤为重要。因此，我将花时间详细解释这一概念。

个人感觉和直观理解 Intuition

假设我们将下面这5个单词转换为嵌入表征：“florida”, “california”, “texas”, “politics”和“truth”。由于嵌入（embeddings）只是由数字组成的数组，我们可以将其绘制在图表上。但是，由于它们的维度（用于表示单词的数字数量）很高，可以轻松达到 100 到 1000，因此我们无法将它们原封不动地绘制出来。我们无法在2维的计算机/手机屏幕上绘制一个100维的向量。此外，人脑很难理解超过3维的东西。4维向量是什么样子的？我不知道。

为了解决这个问题，我们采用了主成分分析（PrincipalComponentAnalysis，PCA[2]）这一降维技术。通过应用PCA，我们可以将嵌入投影到二维空间（x、y坐标）。维度的减少有助于我们在图表上更直观地展现数据。虽然降维后会丢失一些信息，但希望这些降维后的向量仍然能够保持足够的相似性，从而使我们能够深入了解和理解词语之间的关系。

这些数据基于 GloVe 嵌入[3]。

florida = [-2.40062016, 0.00478901]
california = [-2.54245794, -0.37579669]
texas = [-2.24764634, -0.12963368]
politics = [3.02004564, 2.88826688]
truth = [4.17067881, -2.38762552]

也许你会发现这些数字有一些规律可循，但为了方便起见，现在来绘制这些数字。

图中有5个二维向量

在这张图片中，我们能够看到五个二维向量（用x，y坐标表示），分别代表五个不同的单词。正如我们所见，该图示表明了有些单词与其他单词的关联度更高。

数学 math

通过一个简单的方程，我们可以将向量的数学表示与这张图片对应起来。如果您对数学不是特别感兴趣，并且记得《Attention is All You Need》的论文作者将 Transformer 架构描述为“简单的网络架构”，有时候机器学习领域的概念和技术可能会让人感到复杂或难以理解，这可能是真的，但在本文中不会是这样，本文所讨论的内容都是相对简单的。我来解释一下：

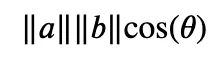
点积计算公式

符号 ||a|| 表示向量 “a” 的大小，它表示从原点（点 0,0）到向量顶端的距离。计算向量大小的公式如下：

向量大小计算公式

计算结果会是一个数字，如 4 或 12.4。

Theta（θ）指的是向量之间的角度（可以看一下上方的图片）。角度的余弦值，表示为cos(θ)，是将余弦函数应用于该角度值的简单结果。

代码 Code

斯坦福大学的研究人员使用 GloVe 算法[3]为这些单词生成嵌入，这些我们在前文讨论过。虽然他们有创建这些嵌入的自有技术，但其基本概念与我们在本系列前一部分中谈到的相同。举个例子，选取 4 个单词，将它们的维度降为 2，然后将它们的向量直接绘制成 x 坐标和 y 坐标。

为了使这个过程顺利运行，下载GloVe[3]是必要的先决条件。

*下面是部分代码，第一个框中的代码，灵感来自于我之前见过的一些代码，但我似乎已经找不到源代码了。

import pandas as pd

path_to_glove_embds = 'glove.6B.100d.txt'

glove = pd.read_csv(path_to_glove_embds, sep=" ", header=None, index_col=0)
glove_embedding = {key: val.values for key, val in glove.T.items()}

words = ['florida', 'california', 'texas', 'politics', 'truth']
word_embeddings = [glove_embedding[word] for word in words]

print(word_embeddings[0]).shape # 100 numbers to represent each word.
---------------------
output:
(100,)

pca = PCA(n_components=2) # reduce dimensionality from 100 to 2.
word_embeddings_pca = pca.fit_transform(word_embeddings)

for i in range(5):
 print(word_embeddings_pca[i])

---------------------
output:
[-2.40062016 0.00478901] # florida
[-2.54245794 -0.37579669] # california
[-2.24764634 -0.12963368] # texas
[3.02004564 2.88826688] # politics
[ 4.17067881 -2.38762552] # truth

现在我们拥有了这5个单词的真实表征，下一步是进行点积计算。

计算向量大小：

import numpy as np

florida_vector = [-2.40062016,  0.00478901]
florida_vector_magnitude = np.linalg.norm(florida_vector)

print(florida_vector_magnitude)
---------------------
output:
2.4006249368060817 # The magnitude of the vector "florida" is 2.4.

计算两个相似向量之间的点积：

import numpy as np

florida_vector = [-2.40062016,  0.00478901]
texas_vector = [-2.24764634 -0.12963368]

print(np.dot(florida_vector, texas_vector))

---------------------
output:
5.395124299364358

计算两个不同向量之间的点积：

import numpy as np

florida_vector = [-2.40062016, 0.00478901]
truth_vector = [4.17067881, -2.38762552]

print(np.dot(florida_vector, truth_vector))

---------------------
output:
-10.023649994662344

从点积计算中可以明显看出，它似乎捕捉并反映了不同概念之间的相似性。

03 缩放点积注意力 Scaled Dot-Product attention

个人感觉和直观理解 Intuition

既然我们已经基本掌握了点积的计算方法，那么就可以开始深入研究注意力机制（attention）了，特别是自注意力机制（self-attention mechanism）。使用自注意力机制使模型能够确定每个单词的重要性，而不管它与其他单词的“物理”距离是多少。这使得模型能够根据每个单词的上下文相关性（contextual relevance）做出比较明智的决策，从而更好地理解单词。

为了实现这一宏伟目标，我们创建了由可学习参数（learnable parameters）组成的3个矩阵，称为查询矩阵（Query）、键矩阵（Key）和值矩阵（Value）（Q、K、V）。查询矩阵（query matrix）可以看作是一个包含用户查询或询问的矩阵（例如，当您询问ChatGPT：“上帝今天下午5点有空吗？（god is available today at 5 p.m.?）”时，这就是查询矩阵）。键矩阵（key matrix）包含序列中的所有其他单词。通过计算这些矩阵之间的点积，我们可以得到每个单词与我们当前正在研究的单词之间的相关程度（例如，翻译或回答用户的询问）。

值矩阵（value matrix）为序列中的每个单词都提供了一种“干净”的表示（“clean” representation）。其他两个矩阵都是以类似的方式形成的，为什么我只说值矩阵“干净（clean）”？因为值矩阵保持在其原始形式，我们不会在与另一个矩阵相乘后使用它，也不会用某个值对它进行归一化处理。这种区别使得值矩阵与众不同，确保它保留了原始的嵌入，无需额外的计算或变换。

这三个矩阵的大小都是word_embedding (512)。不过，它们都被分成了“heads”。在论文中，作者使用了8个“heads”（译者注：heads指的是将注意力机制分解为多个子机制的一种方法。模型可以同时关注输入的不同方面，并从中获取更丰富的信息。这种分解可以增加模型的表达能力和性能。），因此每个矩阵的大小为 sequence_length 乘以64。你可能会问，为什么同样的操作要对 1/8 的数据执行 8 次，而不是对所有数据执行一次。这种方法的理论基础是，通过使用8组不同的权重（如前所述，这些权重是可学习的）进行相同的操作8次，我们可以利用数据中固有的多样性。每个“heads”可以专注于输入中的一个特定方面，总的来说，这可以带来更好的性能。

*在大多数实施方案中，我们实际上并没有将主矩阵分成8份。通过索引，可以实现分割，从而为每个部分实现并行处理。然而，这些只是实现细节。不过，这些只是实现细节。从理论上讲，我们可以用 8 个矩阵完成几乎相同的操作。

我们将查询矩阵Q和键矩阵K进行点积运算，然后将结果除以维度的平方根进行归一化。然后将归一化后的结果通过Softmax函数[4]进行处理，然后将结果与值矩阵V相乘。之所以要对结果进行归一化处理，是因为查询矩阵Q和键矩阵K是以某种随机方式生成的矩阵。它们的维度可能完全不相关（独立），而独立矩阵之间的乘法可能会产生非常大的数值，这可能会对学习效果产生不利影响，我将在本系列的后续部分中解释。

然后，我们使用一种名为Softmax[4]的非线性变换（non-linear transformation），使所有数字的范围介于 0 到 1 之间，并且总和为1。结果类似于概率分布（因为有从0到1的多个结果数字相加得到1）。这些数字体现了序列中每个单词与其他单词的相关性。

最后，我们将结果与矩阵V相乘，就得到了自注意力分数（self-attention score）。

*实际上，编码器由N（在论文中，N=6）个相同的层构成，每个层从上一层获取输入并执行相同的操作。最后一层将数据传递给解码器（我们将在本系列的后续部分中讨论）和编码器的上层。

这是自注意力机制的可视化图像。它就像教室里的一群朋友，有些人与某些人的联系更紧密，有些人与任何人的联系都不太紧密。

图片来自 Vaswani, A. 等人的论文[1]

数学 math

查询矩阵Q、键矩阵K和值矩阵V是通过对嵌入矩阵进行线性变换得到的。线性变换在机器学习中非常重要，如果你对成为一名机器学习从业者感兴趣，我建议你进一步探索这个知识点。本文不会进行深入探讨，但我要说的是，线性变换是一种将向量（或矩阵）从一个空间移动到另一个空间的数学操作。听起来似乎比实际要复杂得多。想象一个箭头指向一个方向，然后移动到右边30度的位置。这就是线性变换的示例。线性变换需要满足一些条件才能被认为是线性的，但现在并不重要。关键是它保留了许多原始向量的特性。

自注意力层的整个计算是通过应用以下公式来完成的：

缩放点积注意力——图片来自 Vaswani, A. 等人的论文[1]

计算过程如下所示：

用Q乘以K的转置（翻转）。
将结果除以矩阵 K 维度数的平方根。
然后有了描述每个单词与其他单词相似程度的“注意力矩阵分数（attention matrix scores）”。将每一行进行 Softmax[4]（非线性）变换。Softmax[4] 有三个有趣的相关功能：

a. 缩放所有数字，使其介于 0 和 1 之间。

b. 使所有数字的和为1。

c. 突出差距，使得稍微更重要的部分变得更加重要。因此，我们现在可以轻松区分模型对单词x1与x2、x3、x4等之间联系的不同感知程度。

4. 将计算出来的分数与矩阵V相乘。这是自注意力机制操作的最终结果。

04 Masking

在本系列的前一章中，我已经解释过我们使用虚拟标记来处理句子中出现的特殊情况，如句子中的第一个单词、最后一个单词等。其中一个标记，表示为，表示没有实际数据，但我们需要在整个过程中保持一致的矩阵大小。为了确保模型理解这些是虚拟标记，并且在自注意力的计算过程中对其不予考虑，我们将这些标记表示为负无穷大（例如一个非常大的负数，例如-153513871339）。掩码值被添加到Q乘以K的乘积结果中。然后，Softmax将这些数字转换为0。这使我们能够在注意力机制（attention mechanism）中有效地忽略虚拟标记，同时保持计算的完整性。

05 Dropout

在自注意力层之后，应用了一种被称为 Dropout 的操作。Dropout是机器学习中广泛使用的一种正则化技术。正则化的目的是在训练过程中对模型施加约束，使其难以过度依赖特定的输入细节。这样，模型就能够更加稳健地学习，并提高其泛化能力。具体实现包括随机选择一些激活值（activations）（来自不同层的输出数字），并将它们置零。在同一层的每次传递中，都有不同的激活值将被置零，从而防止模型根据所获数据找到特定的解决方案。从本质上讲，Dropout有助于增强模型处理不同输入内容的能力，并使模型难以针对数据中的特定模式进行调整。

06 Skip Connection

Transformer架构中的另一个重要操作称为Skip Connection。

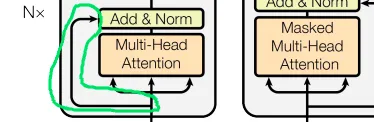
图片来自 Vaswani, A. 等人的论文[1]

Skip Connection是一种在不经过任何转换的情况下传递输入（input）的方法。举例来说，假设我向我的经理报告，而我的经理又向他的经理报告。即使是出于让报告更有用的纯粹目的，输入内容在经过另一个人（或 ML 层）处理时，也会进行一些修改。在这个类比中，Skip Connection就像是我直接向我的经理的经理汇报。因此，上级经理既通过我的经理（经过处理的数据）接收输入，也直接从我这里（未经处理的数据）接收输入。然后，上级经理可以更好地做出决策。采用Skip Connection是为了解决梯度消失等潜在问题，我将在下一节中解释。

07 Add & Norm 层

"Add & Norm"层主要执行加法和归一化操作。我先说加法，因为它比较简单。基本上，我们是将自注意力层的输出与原始输入（通过Skip Connection接收）相加。这个加法是逐元素进行的（每个数字与其相同位置的数字相加）。然后对结果进行归一化。

我们之所以进行归一化处理，原因是每个层都要进行大量计算。数字多次相乘可能会导致意想不到的情况。例如，如果我取一个小数，比如0.3，然后将其与另一个小数，比如0.9相乘，得到的结果是0.27，会比起开始时更小。如果我多次这样做，最终可能会得到非常接近于0的结果。这可能会导致深度学习中的一个问题，即梯度消失。

我现在不想说得太深，以免这篇文章读起来费时费力，但我想说的是，如果数字变得非常接近 0，模型将无法学习。现代机器学习的基础是计算梯度，并使用这些梯度（以及其他一些因素）调整权重。如果这些梯度接近于0，模型将很难有效地学习。

相反，当非小数与非小数相乘时，可能会发生相反的现象，即梯度爆炸（exploding gradients） ，会导致值变得过大。因此，由于权重和激活值的巨大变化，模型的学习会面临困难，从而导致训练过程中的不稳定性和发散性。

机器学习模型有点像小孩子，它们需要保护。保护这些模型免受数字过大或过小的影响的一种方法是归一化。

数学 math

层归一化操作虽然看起来很可怕（一如既往），但实际上相对简单。

图片由 Pytorch 提供，摘自此处[5]

在层归一化操作中，我们需要对每个输入执行以下简单步骤：

从输入中减去其均值。
除以方差的平方根并加上一个epsilon（ε）（一个非常小的数字），用于避免除以零。
将得到的得分乘以一个可学习的参数，称为gamma（γ）。
添加另一个可学习的参数，称为beta（β）。
这些步骤可确保均值接近于0，标准差接近于1。归一化过程增强了训练的稳定性、速度和整体性能。

代码 Code

# x being the input.
(x - mean(x)) / sqrt(variance(x) + epsilon) * gamma + beta

08 总结

至此，我们对编码器的主要内部工作原理有了扎实的了解。此外，我们还探索了Skip Connection，这是机器学习中一种纯粹的技术（也是一种重要的技术），可以提高模型的学习能力。

尽管本节内容有点复杂，但让我们已经对整个 Transformer 架构有了实质性的了解。随着我们在本系列中的进一步深入，理解本部分的内容将有助于你理解本系列中其他部分的内容。

请记住，这是一个前沿领域中的最新技术。学起来并不简单。即使您现在仍然没有完全理解所有内容，您也已经取得了很大的进步！

下一部分将介绍机器学习中的另一个基础（且更简单）的概念，即前馈神经网络。

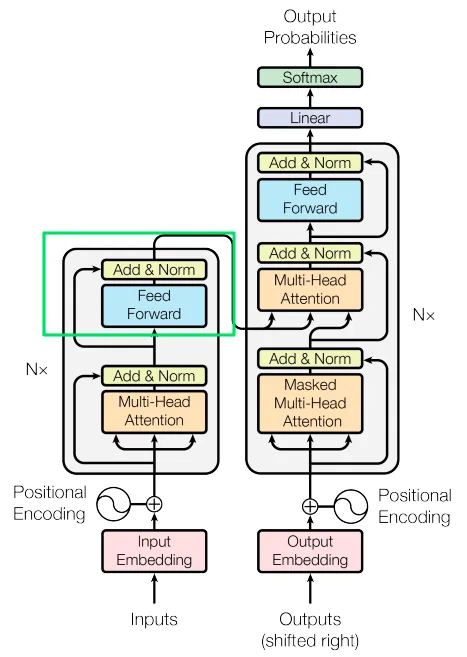
图片来自 Vaswani, A. 等人的论文[1]

END

参考资料

[1]https://proceedings.neurips.cc/paper_files/paper/2017/file/3f5ee243547dee91fbd053c1c4a845aa-Paper.pdf

[2]https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.PCA.html

[3]https://nlp.stanford.edu/projects/glove/

[4]https://docs.scipy.org/doc/scipy/reference/generated/scipy.special.softmax.html

[5]https://pytorch.org/docs/stable/generated/torch.nn.LayerNorm.html

🚢🚢🚢欢迎小伙伴们加入AI技术软件及技术交流群，追踪前沿热点，共探技术难题~