给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1：

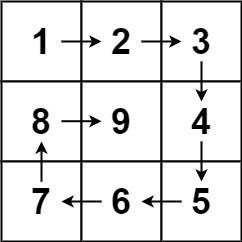
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2：

输入：n = 1
输出：[[1]]

提示：

• 1 <= n <= 20

class Solution {
    public int[][] generateMatrix(int n) {
        int total = n*n;
        int[][] matrix = new int[n][n];
        int row = 0,col=0;
        int count = 1;
        int i = 0;
        while(count <= total){
            //向右
            for(; col < n-i ; col++) {matrix[row][col] = count++;}
            if(count > total) break;
            row+=1;
            col-=1;

            //向下
            for(; row < n-i; ++row) {matrix[row][col] = count++;}
            if(count > total) break;
            col-=1;
            row-=1;
            //if(col < 0) col = 0;
            //向左
            for(; col>= i;--col) {matrix[row][col] = count++;}
            if(count > total) break;
            row-=1;
            col+=1;
            if(row < 0) row = 0;
            //向上
            for(; row > i;--row) {matrix[row][col] = count++;}
            row+=1;
            col+=1;
            if(count > total) break;
            i++;
        }
        return matrix;
    }
}

         每日一题，今天是中等题。

这道题虽然为中等题，但是在我看来，考察的其实只有对边界的控制。螺旋矩阵，我们之前也有题目已经写过。最重要的其实就是找到那4个边界：左边界，右边界，上边界，下边界控制的条件，博主这里用了3个变量来表示这4个边界。当循环一圈之后，可以发现其实上下是对称的，也就是第一排不需要填，最后一排不需要再填，列同理。所以可以用一个i变量来标记循环了几次，就可以知道要填哪一圈，之后就是按照右，下，左，上依次循环处理矩阵，每次循环完，都要记得把循环的列/行复位，因为循环完会比边界多1或者少1，这时候就需要我们人工处理回来。

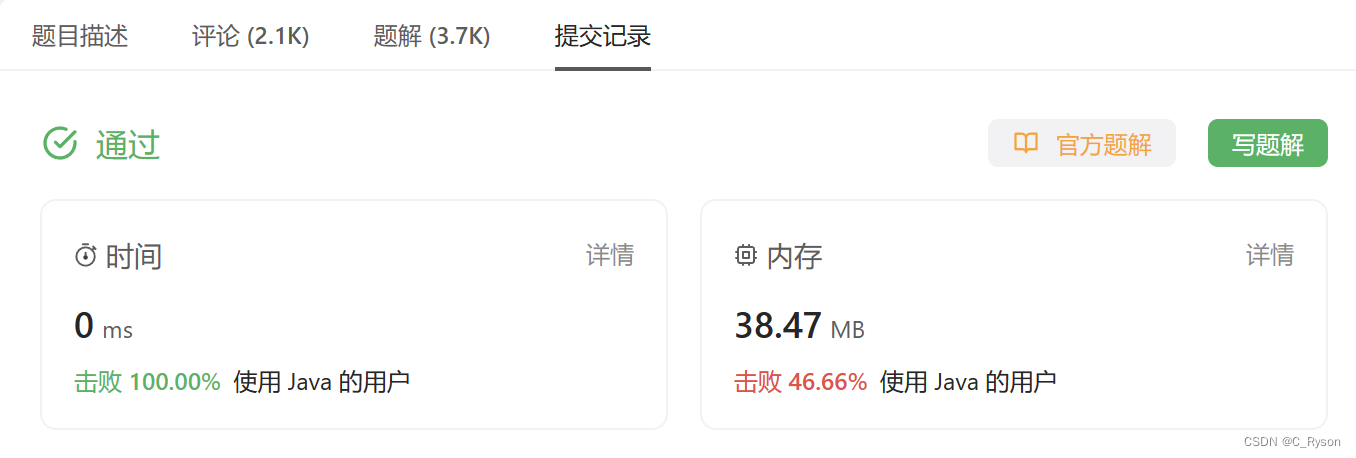
运行结果如下：