大家都知道 “两点确定一线，三点确定一平面”，那么多少个变量可以确定一个分子呢？这是最近顶刊们热烈讨论的话题。
（据笔者不完全统计）最早在 SphereNet （2022 ICLR）论文里，摘要上就开始讨论 completeness 了。后来，ClofNet （2022 ICML）和 ComENet （2022 NeruIPS）直接在标题里就标明 Complete （两个Net名字中的 C 就是 Complete 意思）。

从模型设计角度看，实现 Completeness 似乎成为了提升模型性能的一条捷径。诸多研究小组加入战场，completeness 这个词逐渐演变成了罗生门。在最近的 LEFTNet （2023 NeruIPS）中，作者重新提及 completeness ，似乎能够从一个更高的视角看待这一问题。

本文将首先介绍 SphereNet 和 ClofNet 中有关完备性的观点。两篇论文的作者均花费很多篇幅强调模型的完备性，却没有深入思考 local completeness 如何转化为 global completeness。ComENet 首先意识到了这一点，通过固定两个刚体结构间的旋转键尝试固定整个分支。然而，ComENet 对刚体结构间的相对自由度进行了误判，仅仅考虑了两刚体结构共线平面中的一个自由度，没有将其放在立体的环境中思考。最后，LEFTNet 仔细论证了这一点，补齐了全部三个自由度，最终实现了 Global Completeness。

这篇博客中，我将首先介绍不变模型考虑 Completeness 的代表 SphereNet，向量模型考虑 Completeness 的代表 ClofNet。最后，我将介绍对 local to global 展开讨论的两篇文章 ComENet 和 LEFTNet。

SphereNet 中的 Completeness

在 图神经网络和分子表征：3. 不变网络最后的辉煌-CSDN博客 中我们提到，SphereNet 是 DimeNet 的改进之作。一个朴素的想法是，在引入角度的基础上进一步引入二面角将十分有潜力进一步提高精度。当然，这并非是 AI 研究员首创的想法。

在传统的计算化学领域，距离、角度、二面角所构成的内坐标体系已经被广泛用于改造输入坐标。基于内坐标的几何构型优化被认为大幅降低了势能面的自由度，提高了构型优化的速度。例如，Gaussian 就支持冗余（Redundant）内坐标、z-matrix，广义内坐标（generalized internal coordinates）等关键词。大家感兴趣可以看以下链接中的说明：

z-matrix：

1. 维基百科：https://en.wikipedia.org/wiki/Z-matrix_(chemistry)
2. 一个案例：https://www.chm.bris.ac.uk/pt/ajm/mmhtm/MM_L2p16.htm
3. 优缺点详细解析：https://www.cup.uni-muenchen.de/ch/compchem/geom/internal.html

冗余内坐标（Gaussian 构型优化默认格式）：https://gaussian.com/opt/

广义内坐标：https://gaussian.com/gic/

形式多样内坐标的设计本意是希望3D坐标能够由距离、角度、二面角唯一表示，并能够据此复现出原始结构。如下所示：

SphereNet 原文中多次提到的完备性正是基于这样的理念：

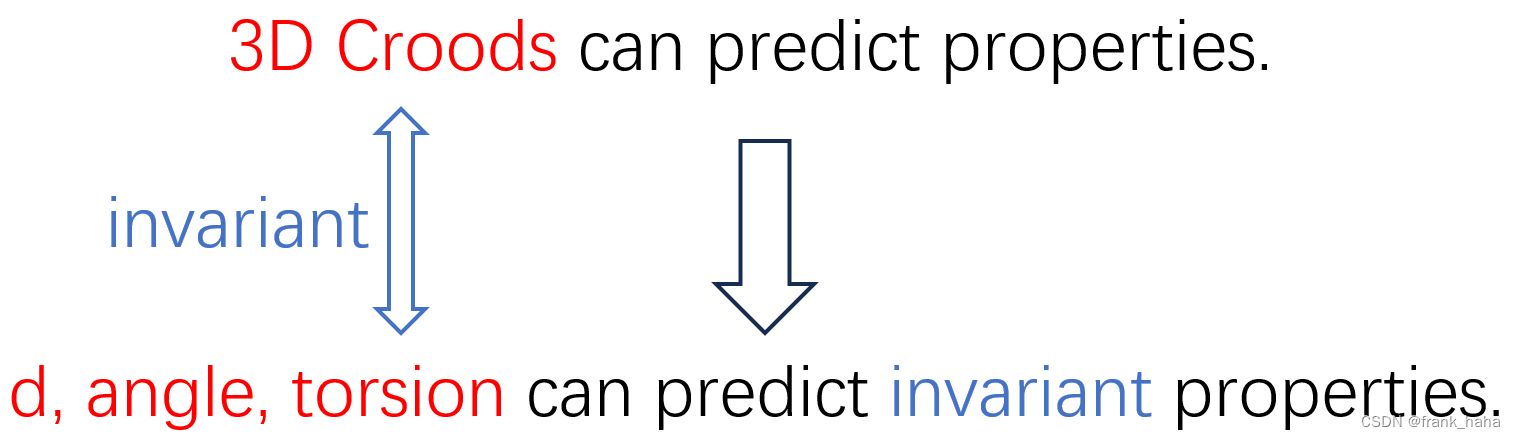
1. 3D 坐标可以预测性质。
2. 3D 坐标能够转化为不变性的距离、角度、二面角。
3. 距离、角度、二面角能够预测不变性质。
   

作者思路可以进一步小结为：之前的模型只是将 3D 坐标转换成了距离和角度，我把二面角添上就完备了，所以一定会有精度提高！具体转换框架见 图神经网络和分子表征：3. 不变网络最后的辉煌-CSDN博客

其实这样的想法忽略了很多问题：

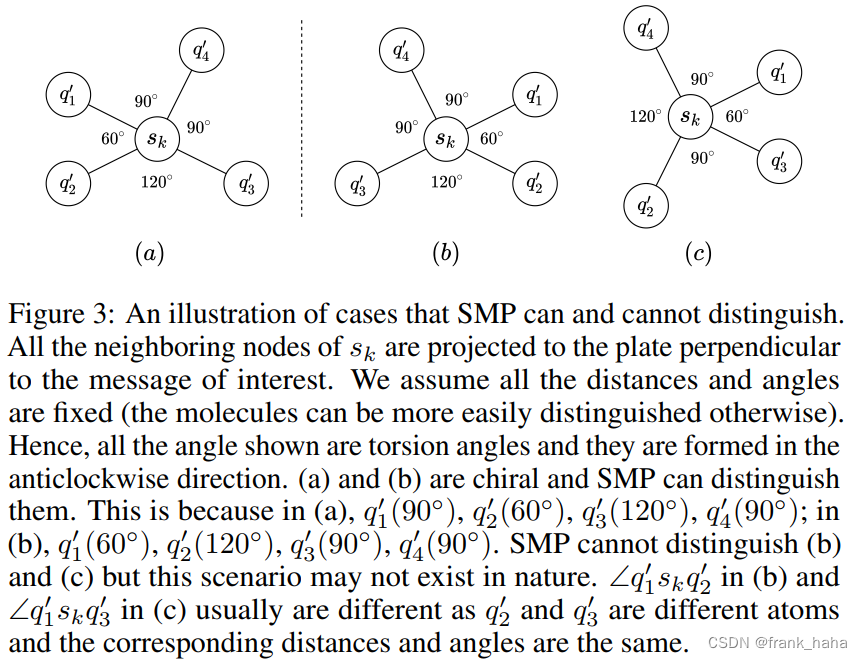
1. 3D 坐标转化为距离、角度、二面角不能有信息损失。换言之，作者设计的转换框架需要有效鉴别所有结构。但是作者在原文就列举了一个反例，作者设计的框架可以鉴别手性分子（下图a,b），但不能鉴别一些特殊案例（下图b,c）：
   

2. 3D 坐标转换为内坐标的方式并非只有唯一解。在 z-matrix 的这个案例中（Internal coordinates of a molecule (bris.ac.uk)），乙烯6个原子，3个原子的确定都涉及了二面角，但是参考平面可以有多种选择。作者在原文指出，GemNet 3-hop 的消息传递模式可以做到完备性，笔者此处表示质疑。如何设计规则拿到正则、完备、物理的几何信息，传统的量子化学软件已经给出了很多解（见上），SphereNet 和 GemNet 显然没有达到上述方法的理论深度。
   

3. 即便转换过程没有损失，消息传递（local to global）过程 也会带来损失。SphereNet 原文完全没有考虑到消息传递（local to global）过程。这一点同样出现在 ClofNet 中，而 ComENet 和 LEFTNet 都对这一过程进行了讨论。

总体来说，SphereNet 中的 Completeness 还是一个 local Completeness。作者的想法就是对 3D 坐标完成不变替代，没有深入考虑后续传递过程。

ClofNet

ClofNet 这个框架本系列还没详细讲过。这篇论文和 LEFTNet 一样，读起来让人非常痛苦。下面就简单介绍下笔者的理解吧。

ClofNet 故事起源

ClofNet 在故事开头指出，现有表征框架无法有效纳入恒电势等真实物理环境。

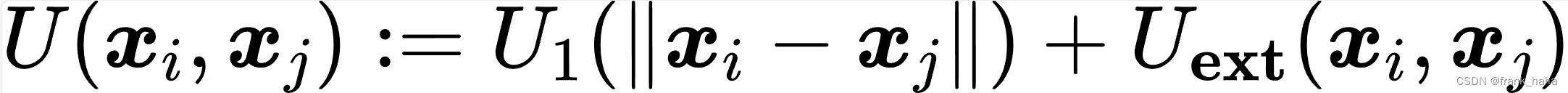
在之前的表征框架中（EGNN），两原子排斥力可以映射到原子向量差上。但原子向量差的形式无法有效反应外加的恒电场。作者指出，如果我们能够建立起一个局域的坐标系，就可以将各种方向的向量标量化。如此以来，我们在消息传递的内部，可以只用标量。

ClofNet 中的 Complete local frame

ClofNet 论文读起来有着对 EGNN 非常明显的模仿痕迹。比如公式 1 直接照搬了 EGNN 的定义

EGNN 本身是一个非常经典的框架，此处碍于笔者的精力，不作展开。

但原作者一个很明显的思路是：EGNN 基于原子坐标向量差去做迭代，只能做原子连线上的性质预测，例如原子受力，类似恒电势就不行。为了解决这个问题，作者拓展了原子坐标向量差的概念：坐标向量差，坐标向量叉乘定义一个平面，加上该平面上的法向向量，三个向量构成了一个正则坐标系。

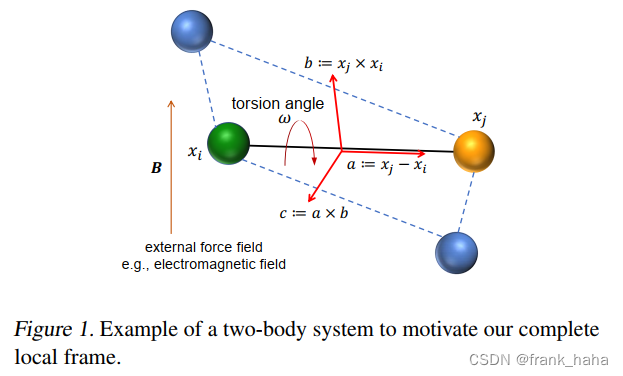
任何有关两原子的向量在该正则坐标系下均有唯一标量坐标，这样即可完成向量向标量的映射。

ClofNet 中的消息传递

写到这里的时候，笔者已经看 ClofNet 这篇论文很久了。这篇论文里的定理证明实在是太多了，这里只放一下笔者粗浅的理解。

一种尝试理解新模型的方式是用已经建立起的框架规则去套。在 On the Expressive Power of Geometric Graph Neural Networks 这篇论文里，作者对 PAINN 做了如下归纳总结：

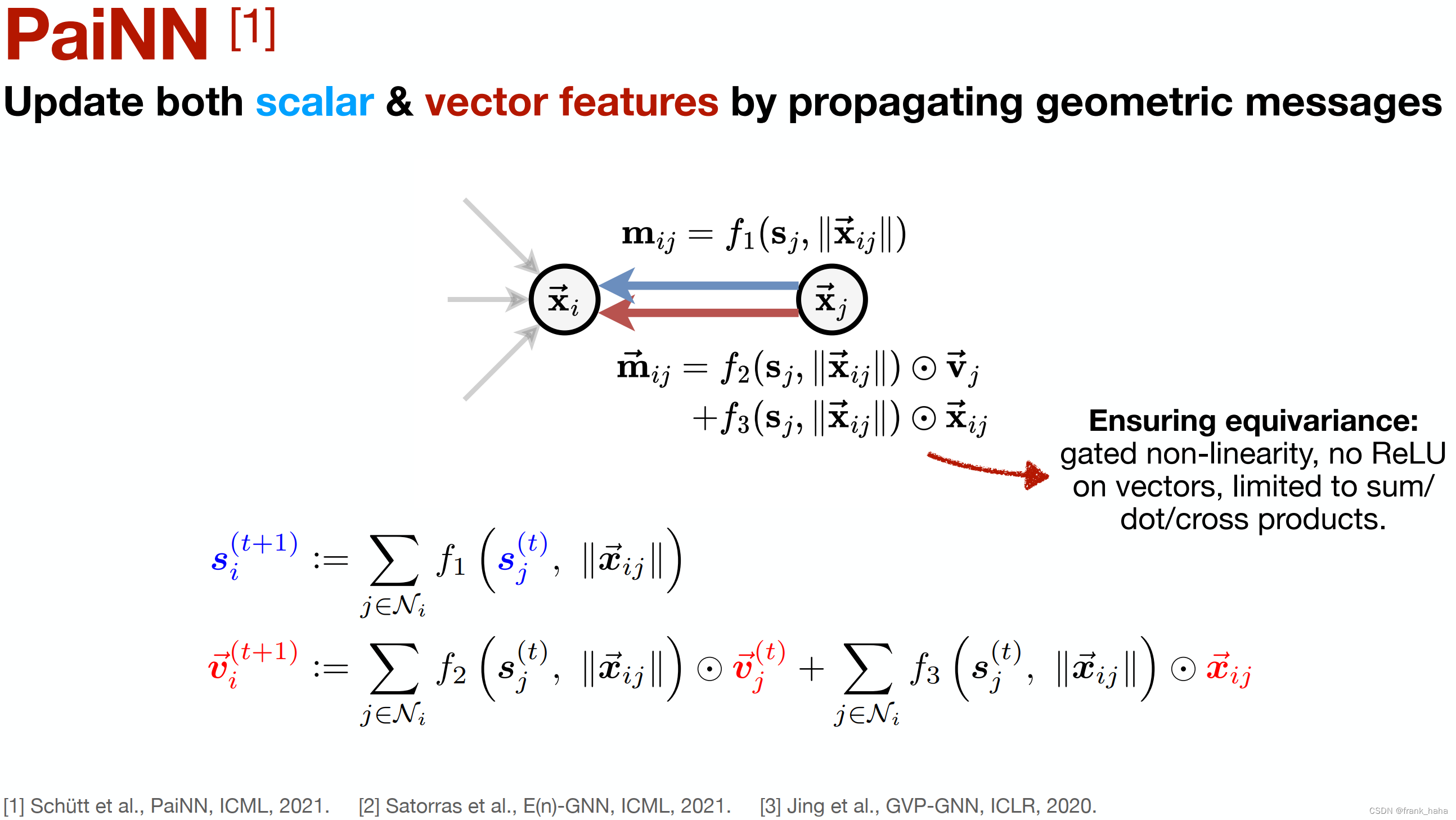
其消息传递过程可以归纳为向量和标量两条平行的路径。

前文已经提到，ClofNet 的消息传递和 EGNN 是基本一致的：

我们从下往上看，第2，3行公式表明 ClofNet 依旧是面向点编程的，将点的性质作为核心的迭代对象。同时，ClofNet 采用和 PAINN 一致的思路，即，标量、向量两条并行的迭代路线。

ClofNet 和 PAINN 的不同之处在于消息本身的设计（第一行），以及消息是如何影响向量性质迭代的（第二行），标量性质的迭代似乎和 PAINN 是一样的。

PAINN 里，消息分为了标量的消息和向量的消息，分别用于标量和向量的迭代。但是 ClofNet 似乎仅有标量的消息，向量的消息通过标量的向量化实现。（第二行）

其实说到这里，把上述三段话中的 ClofNet 换成 EGNN 也完全成立。标量的向量化这个概念已经出现在了 EGNN 的设计框架中。所以，ClofNet 真正的创新在于局域坐标系的建立，进而拓展了向量标量间相互转化这个概念。

现在我们小结一下 ClofNet 的消息传递过程：

1. 从大的视角看， ClofNet 遵从了 PAINN 的设计思想，面向点编程+向量、标量两条平行的迭代路线。我们可以直接套用 PAINN 的图：

   

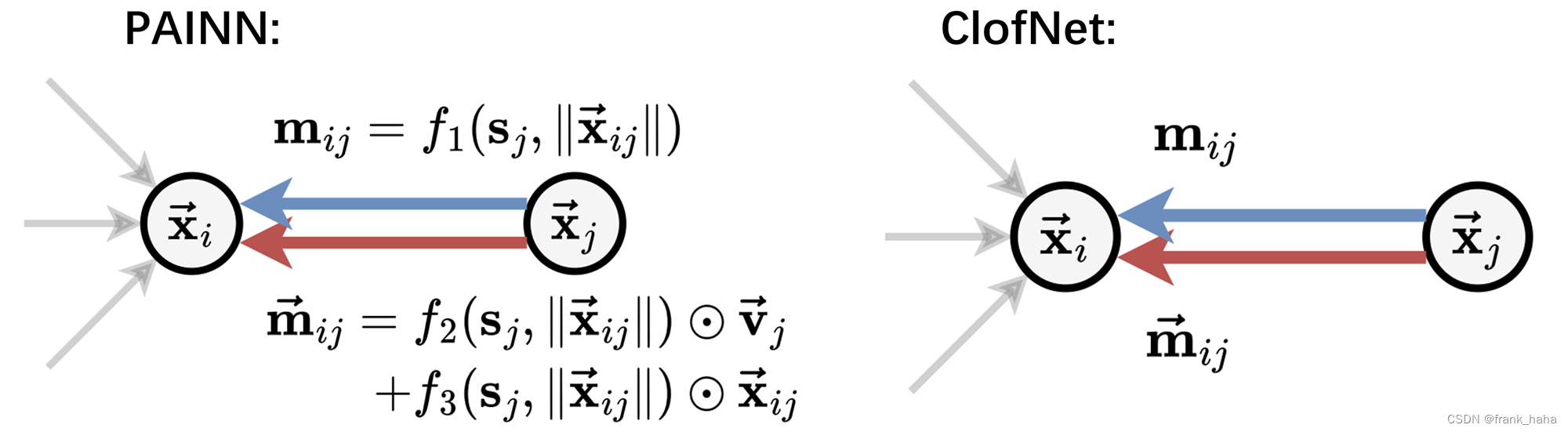
2. 当然，需要把两个 m 的来源抹掉，同时向量 m 依赖于标量 m
   

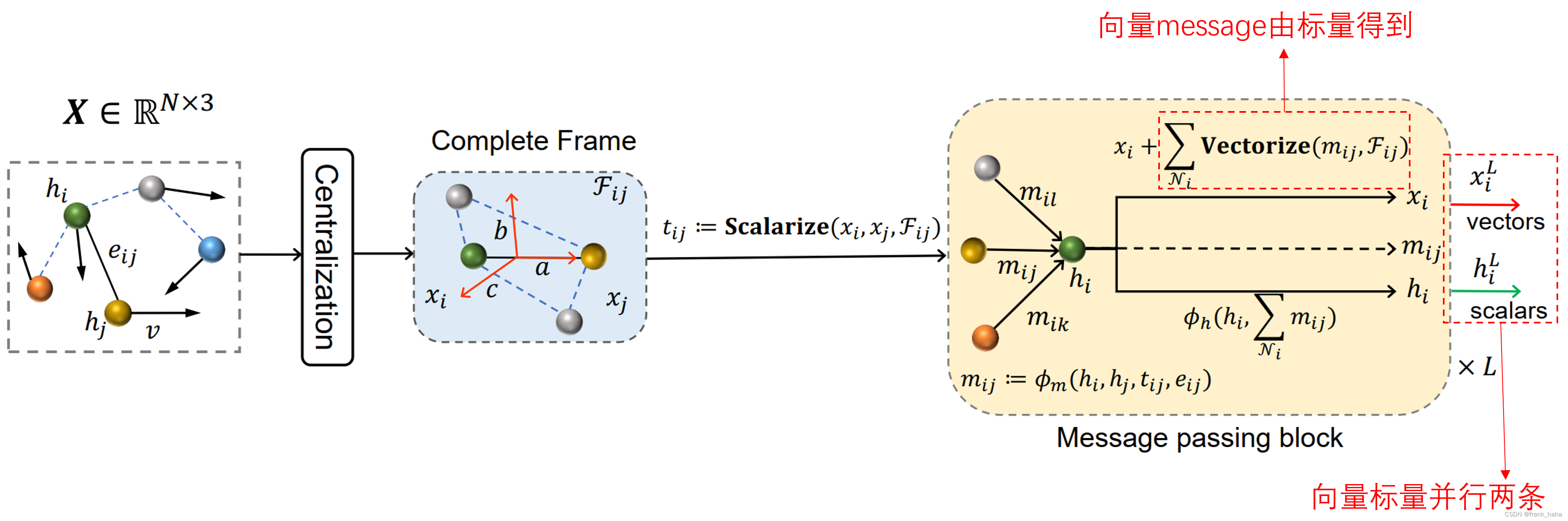
3. 在构建这两个 m 的过程中， ClofNet 设计了一个完备的局域坐标系，将向量标量化，进行迭代计算后再重新向量化。

具体实现细节，请各位读者阅读原文和源码。

ClofNet 中的 Completeness

前文中，我们介绍了 SphereNet 的 Completeness。可以看到，作者十分强调3D坐标向不变几何信息转化的过程中不能出现信息损失。 ClofNet 中并不涉及复杂的多体几何关系， ClofNet 和 PAINN 一样是向量、标量双通路模型。因此，角度、二面角信息隐藏在了向量模型的加减中，无需多虑。笔者认为， ClofNet 中的 Completeness 更多是相对于 EGNN 而言的。因为 EGNN 只能表示原子连线方向的性质（原子相互作用力等），而 ClofNet 则进一步，通过设计局域坐标系，实现了恒电势等向量信息的拟合。意义不在于增加了多少的几何鉴别能力，而是增加了完备的、无损的向量信息拟合能力，因此叫 complete。

值得注意的是，此处的 complete 依然是一个局域的概念，因为作者并没有考虑 local to global 对 Completeness 的影响，这一点在 LEFTNet 中被重点讨论。

ComENet 和 LEFENet 中的 Completeness

ComENet 的消息传递过程在前面博客已经讲过了。图神经网络和分子表征：3. 不变网络最后的辉煌-CSDN博客

在 ComENet 论文的2.2节，作者详细介绍了引入第二个二面角的目的：

1. 在距离+角度+一个二面角的模式下，我们可以做到局域结构的完备性，但这只局限于一近邻的范围。这跟 SphereNet 的思路基本一致 (SphereNet 做到了二近邻的完备性)。
2. 如下图所示，局域坐标系的设定可以将R1和R2两个基团变成刚体（完备性），但是包含R1和R2的整个分支是否是一个刚性结构呢？

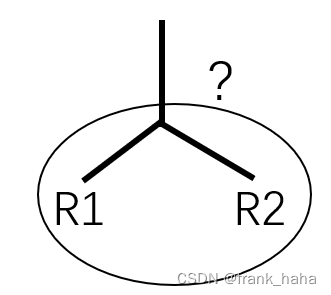
3. 这就是前文多次提到的，local to global 的完备性。ComENet 是这样解释的：i 的 local 是蓝色区域，可以看作上图中的其中一个基团 R1。j 的 local 是黄色区域，可以看作上图基团 R2. 刚性结构 R1 和 R2 间唯一的自由度就是两个刚性结构的夹角，下右图。如果我们把这个夹角固定，整个分支就变成了一个刚性结构。考虑到每个节点都将衍生出一个 local，只要我们能将相邻两个 local 完全冻住，整个体系又是一个连通图，这样整个体系都将被唯一确定。

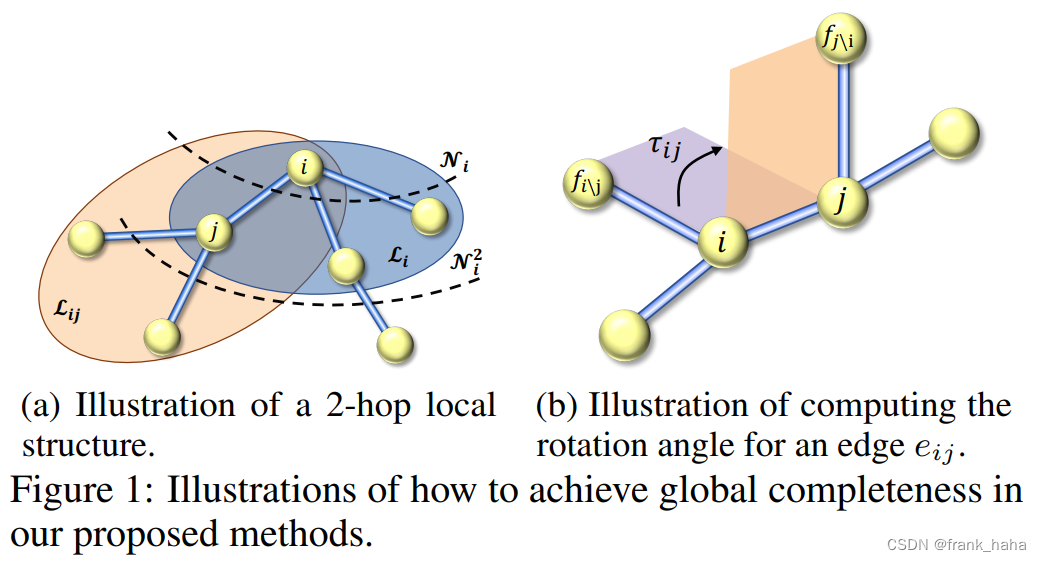
4. 这是 ComENet 中的描述，整个论证过程十分精彩，但是在 LEFTNet 中，作者指出 刚性结构 R1 和 R2 间自由度并不唯一，如果我们在 R1 和 R2 中分别建立局域正交坐标系，那么两个坐标系间的相互转换存在 3 个自由度。 ComENet 描述简化了两个刚体结构。将 刚体结构 R1 简化为了 上右图紫色平面， R2 简化为了上右图黄色平面。如果我们只是平面间的 Freeze，确实只需要一个自由度。但事实是，两个刚体结构都是立体的，我们应该考虑的是两个立体空间相互之间的转换。

5. 如上图所示，作者十分犀利的指出，ComENet 中的 torsion angle 只是两个 local frames 相互转换间的其中一个自由度。
6. LEFTNet 通过设计合理的消息传递机制（FTE）实现了 local to global 的完备性. LEFTNet 的技术细节太多，后面再详细展开。