概述

以前的文章主要描述了神经网络，即多层感知机、全连接模型的运行原理，还是以实验为主，数学描述为辅的方式，这篇文章以纯数学的视角来描述神经网络的运行原理，主要以前馈过程为主（反向传播的动力学过程还是比较复杂，正向过程还未完全研究清楚，暂时还未考虑）。

半空间

在讲半空间（Halfspace）时，需要引入分离超平面（Separating Hyperplane）的概念，这里简单介绍分离超平面的内容。

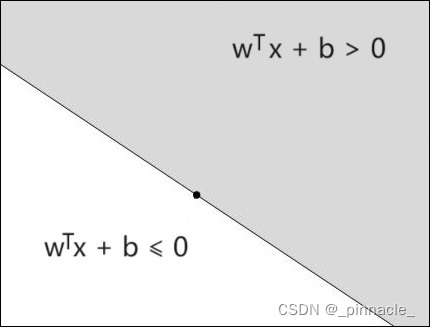
分离超平面是能将两个不相交的凸集分割成两部分的一个平面。在数学中，超平面是 $n$ 维欧氏空间中余维度等于 1 的线性子空间 ， H = { x ∈ R n ∣ w T x + b = 0 } H=\{x\in R^n \mid w^\mathsf{T}x+b = 0\} H={x∈Rn∣wTx+b=0} 就是这样的一个分离超平面。该超平面可以将$n$维欧式空间$R^n$分离为两个半空间。如下图所示：

设置
$$y=w^{\mathsf{T}}x+b$$其中任意半空间可表示为（负半空间）：
S − y = S 0 y = { x ∈ R n ∣ w T x + b ≤ 0 } S_{-}^y=S_{0}^y=\{x\in R^n\mid w^\mathsf{T}x+b \le 0\} S−y​=S0y​={x∈Rn∣wTx+b≤0}或（正半空间）：
S + y = S 1 y = { x ∈ R n ∣ w T x + b > 0 } S_{+}^y=S_{1}^y=\{x\in R^n\mid w^\mathsf{T}x+b \gt 0\} S+y​=S1y​={x∈Rn∣wTx+b>0} * 在本文中，为了公式的简洁，在特定的上下文里，半空间$S$ 的上标 $y$ 可能省略 。

ReLU函数的矩阵表示

因为ReLU良好的数学性质，一般我们使用ReLU作为神经网络的激活函数，其原始形式为：
$$ReLU(x)=max(0,x)$$也可以表示为如下形式：
$$ReLU(x)=\{\begin{array}{cc}1\ast x& ,x>0\\ 0\ast x& ,x\le 0\end{array}$$假设示性函数为:
$$\mathbb{I}(x)=\{\begin{array}{cc}1& ,x>0\\ 0& ,x\le 0\end{array}$$那么ReLU函数可以表示为：
$$ReLU(x)=\mathbb{I}(x)\ast x$$对于有$k$个节点的隐藏层：
$$a=[a^1,a^2,...,a^k{]}^{\mathsf{T}}$$ $$\mathbb{I}(a)=[\mathbb{I}(a^1),\mathbb{I}(a^2),...,\mathbb{I}(a^k){]}^{\mathsf{T}}$$ $$ReLU(a)=Diag(\mathbb{I}(a))a=\left[\begin{array}{cccc}\mathbb{I}(a^1)& & & \\ & \mathbb{I}(a^2)& & \\ & & ...& \\ & & & \mathbb{I}(a^k)\end{array}\right]a$$设${\mathcal{D}}_{\mathbb{I}(a)}=Diag(\mathbb{I}(a))$，即 ${\mathcal{D}}_{\mathbb{I}(a)}$ 将 $\mathbb{I}(a)$ 转换为对角矩阵，可以得到：
$$ReLU(a)={\mathcal{D}}_{\mathbb{I}(a)}\cdot a$$

激活模式

这里为了方便后续的描述，我们将
$$\mathbb{I}(a)=[\mathbb{I}(a^1),\mathbb{I}(a^2),...,\mathbb{I}(a^k){]}^{\mathsf{T}}$$称为激活模式（Activation Pattern），其中任意 I ( a i ) ∈ { 0 , 1 } \mathbb{I}(a^i) \in \{0,1\} I(ai)∈{0,1} ，即 $\mathbb{I}(a)$ 是只包含$0,1$的向量。

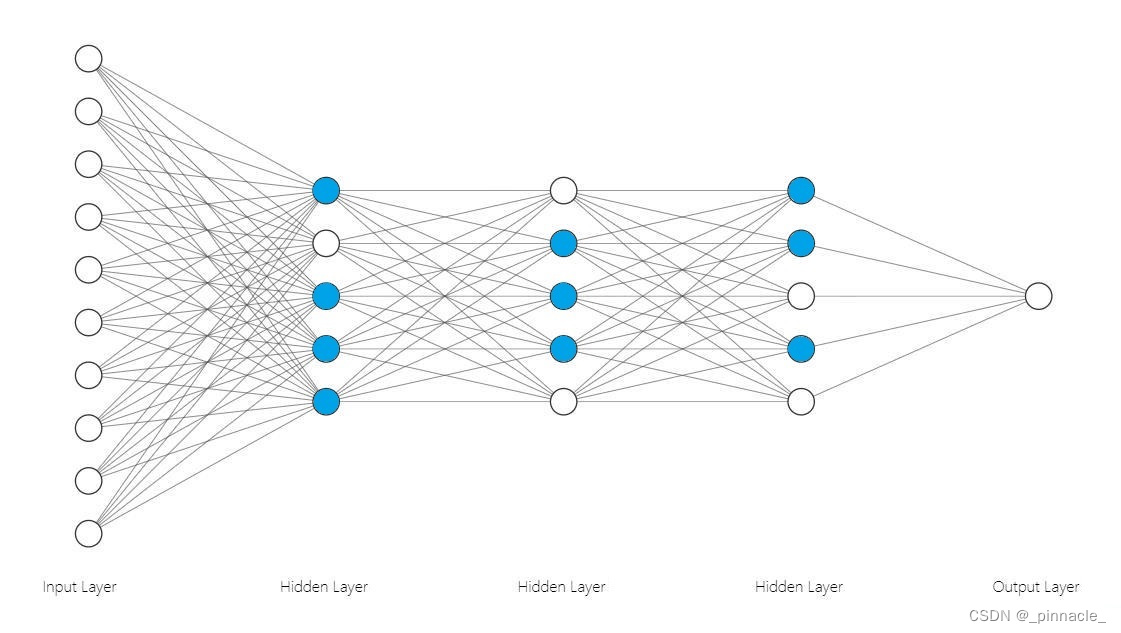
例如，上图中隐藏层的激活模式分别为：
$$\mathbb{I}(a_1)=[1,0,1,1,1{]}^{\mathsf{T}}$$ $$\mathbb{I}(a_2)=[0,1,1,1,0{]}^{\mathsf{T}}$$ $$\mathbb{I}(a_3)=[1,1,0,1,0{]}^{\mathsf{T}}$$

线性区域

线性区域（Linear Region）在以前的文章及参考论文中已经比较好的描述了，线性区域就是使用超平面将输入空间做空间划分（Space Partitioning）得到的区域，这里将其形式化，即用半空间去表示线性区域
如图，$R_i$表示任意的线性区域，$L_i$表示分离超平面。令节点输出：
$$y_i=w_i^{\mathsf{T}}x+b_i$$ 超平面$L_i$可表示为：
L i = { x ∣ w i T x + b i = 0 } L_i =\{x\mid w_i^\mathsf{T}x+b_i = 0\} Li​={x∣wiT​x+bi​=0}对于任意的线性区域$R_j\in R^n$，可以表示为如下形式：
R j = ⋂ y i ∈ { y 1 , y 2 , . . , y n } S I ( y i ) R_j = \textstyle \bigcap_{y_i\in\{y_1,y_2,..,y_n\}} S_{\mathbb{I}(y_i)} Rj​=⋂yi​∈{y1​,y2​,..,yn​}​SI(yi​)​其中 I ( y i ) ∈ { 0 , 1 } \mathbb{I}(y_i) \in \{0,1\} I(yi​)∈{0,1}，例如，对于左图（假设 $L_1$ 右侧为正半空间，$L_2$ 上侧为正半空间）：
$$R_1=S_{+}^{y_1}\bigcap S_{-}^{y_2}$$即线性区域$R_1$表示为$L_1$正半空间与$L_2$负半空间的交集区域，同理可推出其他线性区域的表示。

失活区域

如上图所示 $R_{\varnothing }$ 即表示失活区域（Dead Region），这里失活区域是，当某个线性区域在所有超平面的负半空间时：
R j = ⋂ y i ∈ { y 1 , y 2 , . . , y n } S − y i R_j = \textstyle \bigcap_{y_i\in\{y_1,y_2,..,y_n\}} S^{y_i}_{-} Rj​=⋂yi​∈{y1​,y2​,..,yn​}​S−yi​​ 该区域在隐藏层中因为ReLU的作用，所有节点都会输出 0 值，这时下层网络将无法再次将该区域作空间划分，换句话说，这时下层网络的秩为0，即：
$$r_{\iota }=rank(w_{\iota }^{\mathsf{T}}{\mathcal{D}}_{\mathbb{I}(a_{\iota -1})})=0$$这时，该层网络会将该区域压缩到零空间，该区域将不能再次被下一层线性分离。

线性区域的激活模式

简单的说，每一个线性区域都会对应一组激活模式。比如对于上图$R_1$区域，对应的是$y_1$节点的正半空间与$y_2$节点的负半空间的交集。所以它的激活模式可以直接根据定义给出：
$$\mathbb{I}(a)=[\mathbb{I}(S_{+}^{y_1}),\mathbb{I}(S_{-}^{y_2}){]}^{\mathsf{T}}=[1,0{]}^{\mathsf{T}}$$ 即该激活模式直接代表该线性区域，或者说当产生该激活模式时，表示该线性区域被激活。

当考虑下一层网络时，下一层网络实际是在该激活的线性区域内（仿射变换后的数据上），再次做空间划分，即递归的空间划分。

多层隐藏层的线性区域

单层隐藏层

每一层的隐藏层是比较好理解的，和上面相同，使用$k$个超平面将输入空间划分为有限个线性区域。这里的输入空间在每一层都是不同的，比如：对第一层隐藏层，它的输入空间就是原始输入空间。对于后续层都是在原始输入空间，经过一次或多次仿射变换后的局部输入空间。

多层隐藏层

在这里我们主要讨论整个网络在原始输入空间的线性区域，对于有$N$层的神经网络，第 $\iota$ 层有$k$个输出节点可以表示为：
$$a_{\iota }=w_{\iota }^{\mathsf{T}}{x}_{\iota -1}+b_{\iota }$$ $$x_{\iota }={\mathcal{D}}_{\mathbb{I}(a_{\iota })}\cdot a_{\iota }$$其中$\iota \ge 1,x_0$为原始输入，也可以将网络表示为从输入层开始的网络：
$$x_{\iota }=\prod _{i=1}^{\iota }{\mathcal{D}}_{\mathbb{I}(a_i)}\cdot a_i$$这里定义 $R(x_{\iota }\to x_0)$ 为第 $\iota$ 层输出 $x_{\iota }$ 映射到$x_0$的线性区域，那么我们可以得到：
$$R(x_{\iota }\to x_0)=\{\begin{array}{cc}{R}^n& ,\iota =0\\ {\bigcap }_{i=1}^k{S}_{\mathbb{I}(a_{\iota }^i)}\bigcap R(x_{\iota -1}\to x_0)& ,\iota \ge 1\end{array}$$ 所以对于每一层不同的激活模式，其映射到原始数据输入空间的区域都是不同的。整个网络的激活模式组合表示的是一个特定的激活区域。

隐藏层的秩

我们注意到，对于除第一层的隐藏层其参数矩阵的秩，并不是该层真正的秩，如对于第$\iota$ 层参数，其秩并不是$w_{\iota }$的秩，而是与上一层共同表示的，即：
$$rank(w_{\iota })\ne rank(w_{\iota }^{\mathsf{T}}{\mathcal{D}}_{\mathbb{I}(a_{\iota -1})})$$而 ${\mathcal{D}}_{\mathbb{I}(a_{\iota -1})}$ 会根据不同输入动态变化，所以该层的秩是动态变化的，为 $rank(w_{\iota }^{\mathsf{T}}{\mathcal{D}}_{\mathbb{I}(a_{\iota -1})})$，且：
$$rank(w_{\iota })\ge rank(w_{\iota }^{\mathsf{T}}{\mathcal{D}}_{\mathbb{I}(a_{\iota -1})})$$换句话说，ReLU激活函数的一个附带作用就是动态改变该层网络的秩。

全连接层的线性区域

全连接（分类）层的逻辑和隐藏层是不同的，隐藏层由于ReLU激活函数的作用，节点直接构成超平面。而对于全连接层而言，其激活函数一般为softmax，而最后一般我们使用的是max函数获取激活值最大的节点，即它本身表示的是 max 或 maxout 过程，即：
$$g(y_1,y_2,...,y_n)=max(y_1,y_2,..,y_n)$$ 对于有 $n$ 个节点的全连接层
$$y_i=w_i^{\mathsf{T}}x+b_i$$ 其中 i ∈ { 1 , 2.. , n } i\in \{1,2..,n\} i∈{1,2..,n}，对于任意节点 y k ∈ { y 1 , y 2 . . , y n } y_k\in \{y_1,y_2..,y_n\} yk​∈{y1​,y2​..,yn​} ，若 $y_k$ 为最大值的节点，则要求对于 ∀ y i ∈ { y 1 , y 2 . . , y n } ∖ y k \forall y_i \in \{y_1,y_2..,y_n\} \setminus y_k ∀yi​∈{y1​,y2​..,yn​}∖yk​，$y_k>y_i$ 恒成立，所以全连接层的超平面是节点间比较产生的。此时 $y_k$ 关联的超平面排列（Hyperplane Arrangements）为：
H k = { y ( k , 1 ) = 0 , y ( k , 2 ) = 0 , . . . , y ( k , n ) = 0 } H_k=\{y_{(k,1)}=0,y_{(k,2)}=0,...,y_{(k,n)}=0\} Hk​={y(k,1)​=0,y(k,2)​=0,...,y(k,n)​=0}其中
$$y_{(k,i)}=y_k-y_i=(w_k-w_i{)}^{\mathsf{T}}x+(b_k-b_i)$$ 这里 k ∈ { 1 , 2.. , n } ∖ i k\in \{1,2..,n\}\setminus i k∈{1,2..,n}∖i，对任意的节点，其对应的线性区域，可表示为：
R k = ⋂ y ~ ∈ { y ( k , 1 ) , y ( k , 2 ) , . . . , y ( k , n ) } S + y ~ R_k=\textstyle \bigcap_{\tilde{y} \in\{y_{(k,1)},y_{(k,2)},...,y_{(k,n)}\}} S^{\tilde{y}}_{+} Rk​=⋂y~​∈{y(k,1)​,y(k,2)​,...,y(k,n)​}​S+y~​​ 这里 $S_{+}^{\tilde{y}}$ 表示 $\tilde{y}=0$ 所分离的正半空间。例如，下图是一个3节点的全连接网络的各节点关联超平面排列的正半空间求交集所获取的线性区域。

n维空间的子集

虽然一般我们将输入空间定义在$n$维的实数空间，但实际我们的输入数据都会被限制到有界的封闭的定义区间内，即某个$n$维空间的子集内部。比如图像数据被限制为$n$维的，每一维数据的值$x_i\in [0,255]$的区间范围，或者归一化到$x_i\in [0,1]$的区间内，简单来说就是$n$维的超长方体（Super Cuboid）。该子集可以表示为如下形式：
U = { ( x 1 , x 2 , . . . , x n ) ∈ R n ∣ x i ∈ [ 0 , 1 ] , i ∈ { 1 , . . . , n } } U = \{ (x_1,x_2,...,x_n)\in R^n \mid x_i \in [0,1],i \in\{1,...,n\} \} U={(x1​,x2​,...,xn​)∈Rn∣xi​∈[0,1],i∈{1,...,n}} 这里的$U$即为在$n$维空间的子集，也是通常模型真正的输入空间（Input Space）。

冗余节点

从以上线性区域的定义可知，当已知任意隐藏层所有节点表示的超平面（节点超平面）时，其线性区域可表示为：
R j = ⋂ y i ∈ { y 1 , y 2 , . . , y n } S I ( y i ) R_j = \textstyle \bigcap_{y_i\in\{y_1,y_2,..,y_n\}} S_{\mathbb{I}(y_i)} Rj​=⋂yi​∈{y1​,y2​,..,yn​}​SI(yi​)​其中 I ( y i ) ∈ { 0 , 1 } \mathbb{I}(y_i) \in \{0,1\} I(yi​)∈{0,1} 且 $y_i=w_i^{\mathsf{T}}x+b_i$，那么对于某一个节点 $y_k$
$$R_k=S_{\mathbb{I}(y_k)}$$ R z = ⋂ y i ∈ { y 1 , y 2 , . . , y n } ∖ y k S I ( y i ) R_z = \textstyle \bigcap_{y_i\in\{y_1,y_2,..,y_n\} \setminus y_k} S_{\mathbb{I}(y_i)} Rz​=⋂yi​∈{y1​,y2​,..,yn​}∖yk​​SI(yi​)​命题 1：对于任意激活模式，都有 $R_z\subseteq U,R_k\bigcap U=\varnothing$，那么 $y_k$ 为冗余节点。

证明：当$R_k\bigcap U=\varnothing$ 时，对于任意的输入$x\in U$，$\mathbb{I}(y_k)=0$，对于下一层输出
y ~ = w T ( D I ( y ) ⋅ y ) + b = I ( y k ) ∗ w k ∗ y k + b + ∑ i ∈ { 1 , 2 , . . , n } ∖ k I ( y i ) ∗ w i ∗ y i \tilde{y} =w^\mathsf{T}( \mathcal{D}_{\mathbb{I}(y)}\cdot y)+b=\mathbb{I}(y_k)*w_k*y_k+b+\sum_{i\in\{1,2,..,n\}\setminus k} \mathbb{I}(y_i)*w_i*y_i y~​=wT(DI(y)​⋅y)+b=I(yk​)∗wk​∗yk​+b+i∈{1,2,..,n}∖k∑​I(yi​)∗wi​∗yi​ ⇒ y ~ = b + ∑ j ∈ { 1 , 2 , . . , n } ∖ k I ( y j ) ∗ w j ∗ x j \Rightarrow \tilde{y} = b+\sum_{j\in\{1,2,..,n\}\setminus k} \mathbb{I}(y_j)*w_j*x_j ⇒y~​=b+j∈{1,2,..,n}∖k∑​I(yj​)∗wj​∗xj​这里$y_k$节点被消去，所以$y_k$节点不影响下一层输出，即$y_k$ 为冗余节点。

流形

待续…

总结

通过本篇文章，希望大家能理解神经网络的数学原理，如有错误请不吝指出（先发后改，后面有新的内容会补充）。

参考文献

1. On the Number of Linear Regions of Deep Neural Networks
2. On the number of response regions of deep feed forward networks with piece- wise linear activations
3. On the Expressive Power of Deep Neural Networks
4. On the Number of Linear Regions of Convolutional Neural Networks
5. Bounding and Counting Linear Regions of Deep Neural Networks
6. Multilayer Feedforward Networks Are Universal Approximators
7. Facing up to arrangements: face-count formulas for partitions of space by hyperplanes
8. An Introduction to Hyperplane Arrangements
9. Combinatorial Theory: Hyperplane Arrangements
10. Partern Recognition and Machine Learning
11. Convex Optimization
12. Scikit-Learn Decision Tree
13. Neural Networks are Decision Trees
14. Unwrapping All ReLU Networks
15. Unwrapping The Black Box of Deep ReLU Networks:Interpretability, Diagnostics, and Simplification
16. Any Deep ReLU Network is Shallow
17. How to Explain Neural Networks: an Approximation Perspective
18. Deep ReLU Networks Have Surprisingly Few Activation Patterns