作者:BENJAMIN TRENT
什么是标量量化以及它是如何工作的?

大多数嵌入模型输出 float32 向量值。 虽然这提供了最高的保真度,但考虑到向量中实际重要的信息,这是浪费的。 在给定的数据集中,嵌入永远不需要每个单独维度的所有 20 亿个选项。 对于高维向量(例如 386 维及更高维)尤其如此。 量化允许以有损方式对向量进行编码,从而稍微降低保真度并节省大量空间。
桶里的乐趣
标量量化采用每个向量维度并将它们分成一些较小的数据类型。 对于博客的其余部分,我们将假设将 float32 值量化为 int8。 要准确地对值进行分桶,并不像将浮点值四舍五入到最接近的整数那么简单。 许多模型输出的向量的维度连续在 [−1.0,1.0] 范围内。 因此,两个不同的向量值 0.123 和 0.321 都可以向下舍入为 0。最终,向量将仅使用 int8 中 255 个可用存储桶中的 2 个,丢失太多信息。
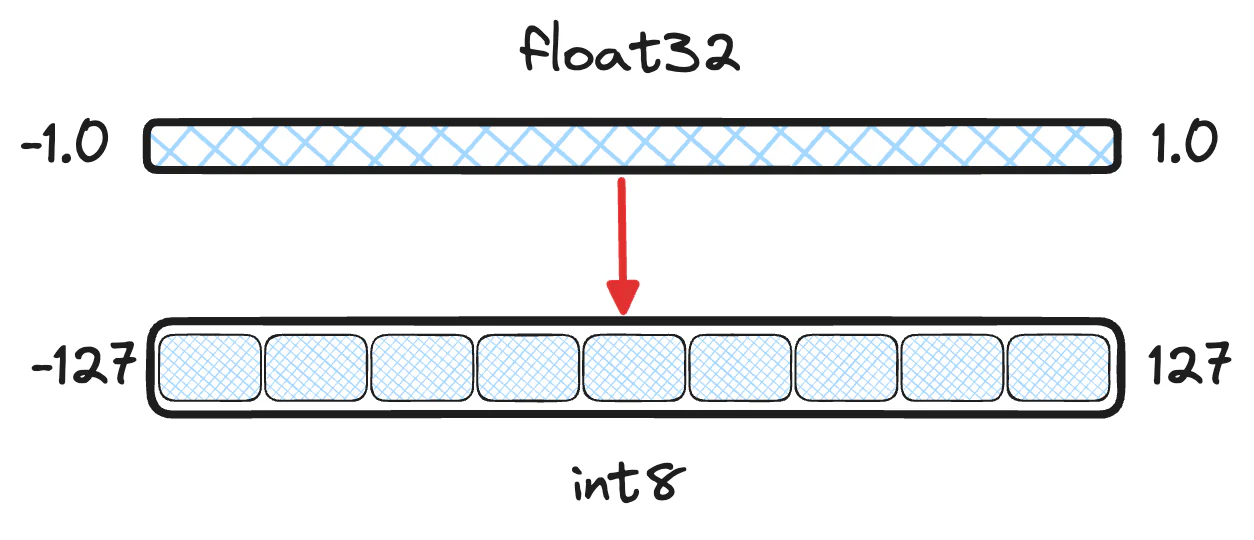
数值转换背后的数学并不太复杂。 由于我们可以计算浮点范围的最小值和最大值,因此我们可以线性移动这些值,然后对中间的值进行存储。

桶里的乐趣
分位数 (quantile) 是包含一定百分比值的分布切片。 所以,举例来说,我们的浮点值可能有 99% 都在 [−0.75, 0.86] 之间,而不是真正的最小值和最大值 [−1.0,1.0] 之间。 任何小于 -0.75 和大于 0.86 的值都被视为异常值。 如果你在尝试量化结果时包含异常值,则最常见值的可用存储桶将会减少。 更少的存储桶意味着更低的准确性,从而导致更大的信息损失。
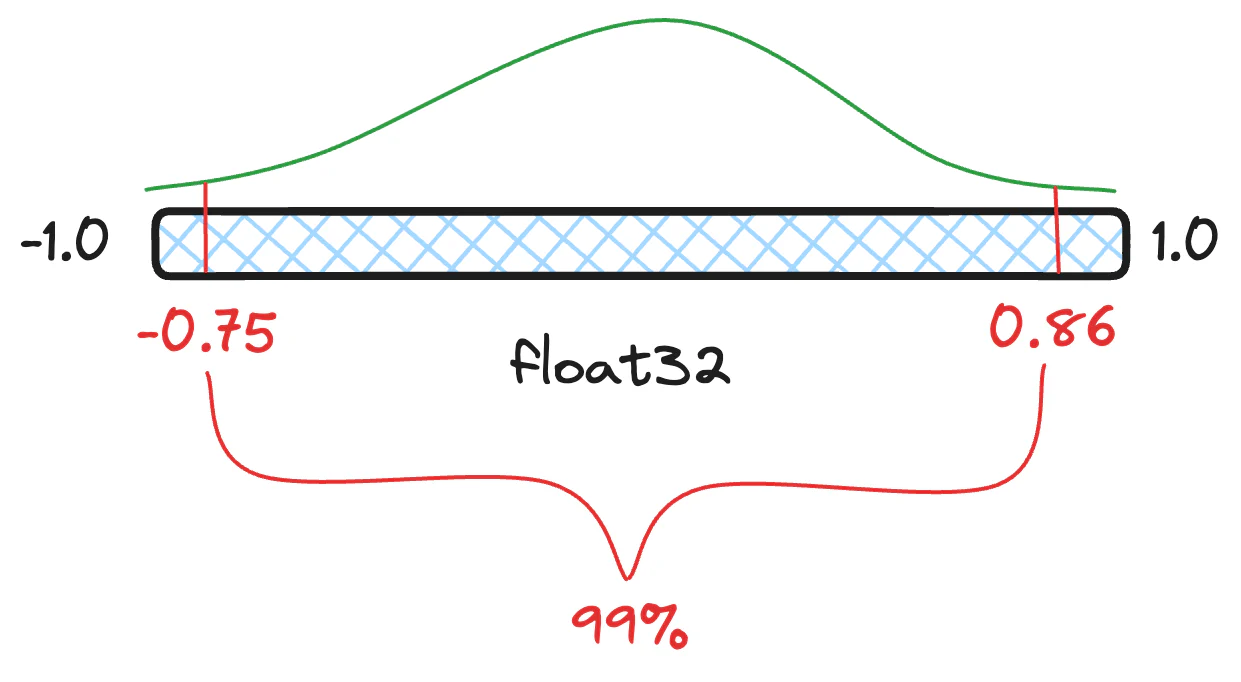
这一切都很好,但是既然我们知道如何量化值,那么我们如何实际计算两个量化向量之间的距离呢? 它和普通的点积 (dot_product) 一样简单吗?
是时候记住你的代数了
我们仍然缺少一个重要的部分,即如何计算两个量化向量之间的距离。 虽然我们在这个博客中还没有回避数学,但我们即将做更多的事情。 是时候拿出你的铅笔来尝试记住多项式和基本代数了。
dot_product 和 cosine 相似度的基本要求是能够将浮点值相乘并将它们的结果相加。 我们已经知道如何在 float32 和 int8 值之间进行转换,那么我们的转换中的乘法是什么样的呢?
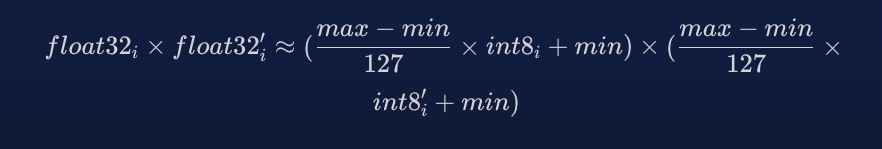
然后我们可以展开这个乘法,为了简化,我们将用 α 代替 (max-min)/127

更有趣的是,这个方程只有一部分需要同时使用两个值。 然而,dot_product 不仅仅是两个浮点数相乘,而是向量每个维度的所有浮点数相乘。 有了向量维度计数 dim,以下所有内容都可以在查询时和存储时预先计算。

并且可以存储为单个浮点值。

可以预先计算并存储为单个浮点值或在查询时计算一次。
![]()
可以预先计算并存储为单个浮点值。
所有这一切:
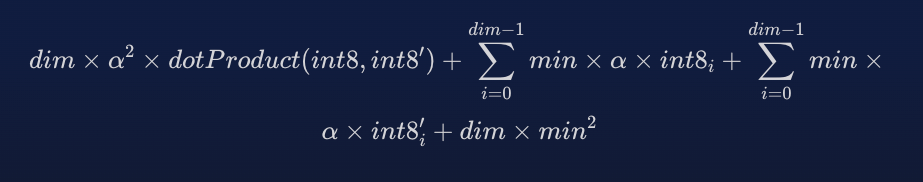
dot_product 所需的唯一计算就是 dotProduct(int8,int8′) 以及一些预先计算的值与结果相结合。
但是,这如何准确呢?
那么,这到底有多准确呢? 我们不会因为量化而丢失信息吗? 是的,我们是,但是量化利用了我们不需要所有信息的事实。 对于学习嵌入模型,各个维度的分布通常不存在肥尾 (fat-tails)。 这意味着它们是本地化的并且相当一致。 此外,通过量化每个维度引入的误差是独立的。 这意味着,对于我们典型的向量运算(如 dot_product)来说,错误被抵消了。
结论
哇,这真是太多了。 但现在你已经很好地掌握了量化的技术优势、其背后的数学原理,以及如何在考虑线性变换的同时计算向量之间的距离。 接下来看看我们如何在 Lucene 中实现这一点,以及其中的一些独特的挑战和优势。