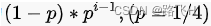redis6.0源码分析：跳表skiplist

news2024/11/27 18:34:56

文章目录

  • 前言
  • 什么是跳表
  • 跳表（redis实现）的空间复杂度
    • 相关定义
  • 跳表（redis实现）相关操作
    • 创建跳表
    • 插入节点
    • 查找节点
    • 删除节点

前言

太长不看版

  • 跳跃表是有序集合zset的底层实现之一， 除此之外它在 Redis 中没有其他应用。
  • 每个跳跃表节点的层高都是 1 至 64 之间的随机数。
  • 层高越高出现的概率越低，层高为i的概率为在这里插入图片描述
  • 跳跃表中，分值可以重复， 但对象成员唯一。分值相同时，节点按照成员对象的大小进行排序。

本篇解析基于redis 5.0.0版本，本篇涉及源码文件为t_zset.c，server.h。

什么是跳表

跳表是一个随机化的数据结构，实质就是一种可以进行二分查找的有序链表。

我们都知道在有序数组中进行查找，可以使用二分查找，将时间复杂度降为O(log n)。但是有序链表做不到，是因为有序链表获取某元素复杂度为O(n)，无法通过二分的思想去跳过一些元素的访问。

例如下图要查找元素50,就必须 5 -> 6 -> 10 -> 30 -> 49 这样去找，而不能说先看 中心元素49小于50，则开始从中心右边开始查找，跳过元素5，6，10， 30的访问。

在这里插入图片描述

而跳跃表则是通过在节点中提取索引的方式，实现有序链表的快速查找。本质上是一个空间(额外的步进指针)换时间的操作。例如下图：

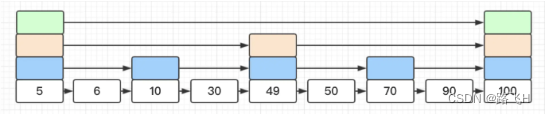
在这里插入图片描述

这时查找元素50变成了 5 -> 49,略过了中间元素6，10， 30。上图中通过首节点存储不同步长的指针将链表完美二分，但是实际上的跳表却类似与下面这张图的结构,大部分情况喜爱不是完美二分的：

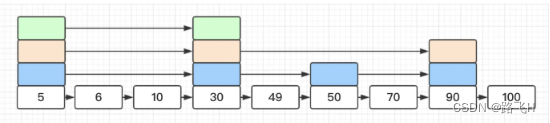
在这里插入图片描述

跳跃表采用了随机算法(层高越高概率越小)来决定层高，相同层之间通过指针相连。redis实现中某节点层高为i的概率为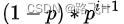在这里插入图片描述

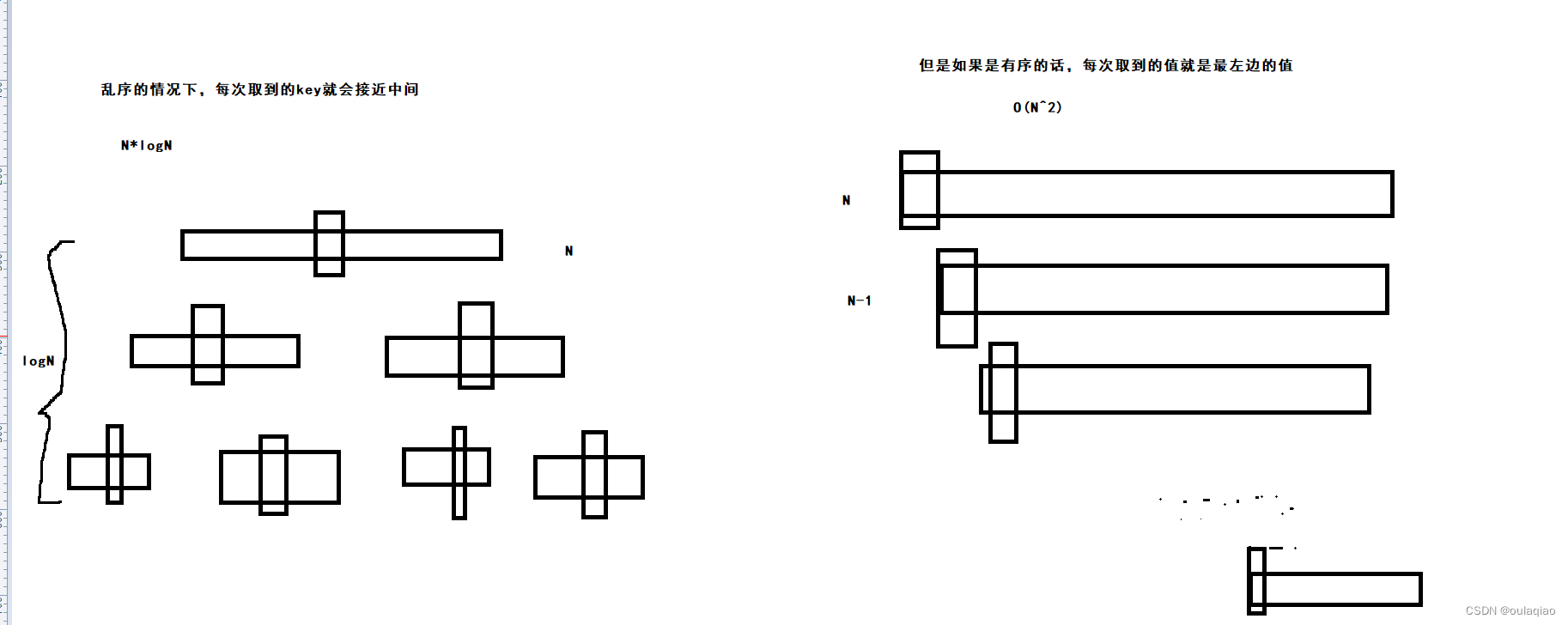
为什么不采用最完美的二分结构？

考虑一下，插入节点的情况。当中间插入一个节点，此时的二分结构会被打破，所以需要不断的进行调整。想想平衡树，红黑树复杂的再平衡操作，而此处的再平衡调整比之有过之而无不及。而使用随机算法进行层高选择的方法也可以实现O(logN)的平均复杂度，而且操作也相对简化的很多。

跳表（redis实现）的空间复杂度

相关定义

// 层高最大值限制
#define ZSKIPLIST_MAXLEVEL 64 /* Should be enough for 2^64 elements */
// 层高是否继续增长的概率
#define ZSKIPLIST_P 0.25      /* Skiplist P = 1/4 */
// 跳表节点定义
typedef struct zskiplistNode {
    // 存储内容
    sds ele;
    // 分值,用于排序
    double score;
    // 后退指针
    struct zskiplistNode *backward;
    // 变长数组，记录层信息。层高越高跳过的节点越多(因为层高越高概率越低)
    struct zskiplistLevel {
        // 指向当前层下一个节点
        struct zskiplistNode *forward;
        // 当前节点与forward所指节点中间节点数
        unsigned long span;
    } level[];
} zskiplistNode;
// 跳表结构管理节点
typedef struct zskiplist {
    struct zskiplistNode *header, *tail;
    // 长度
    unsigned long length;
    // 跳表高度(所有节点最高层高)
    int level;
} zskiplist;

int zslRandomLevel(void) {
    // 计算当前插入元素层高的随机函数
    int level = 1;
    // (random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF) 概率为1/4
    while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF))
        level += 1;
    return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
}

层高为1概率为 1-p(不进while)

层高为2的概率为 p(进一次while) * (1 - p)(不进while)

层高为3的概率为 p(进一次while) * p(进一次while) * (1 - p)(不进while)

…

层高为n的概率为 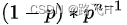在这里插入图片描述

层高的期望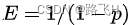在这里插入图片描述

在概率论和统计学中，数学期望(mean)（或均值，亦简称期望）是试验中每次可能结果的概率乘以其结果的总和，是最基本的数学特征之一。它反映随机变量平均取值的大小

在redis实现中 p=1/4, 层高期望为E约等于1.33，所以节点的平均层高约等于1.33是个常数，从而得出跳跃表的空间复杂度为O(n)。

跳表（redis实现）相关操作

创建跳表

zskiplistNode *zslCreateNode(int level, double score, int ele) {
    zskiplistNode *zn =
        malloc(sizeof(*zn)+level*sizeof(struct zskiplistLevel));
    zn->score = score;
    zn->ele = ele;
    return zn;
}

/* Create a new skiplist. */
zskiplist *zslCreate(void) {
    int j;
    zskiplist *zsl;

    zsl = malloc(sizeof(*zsl));
    zsl->level = 1;
    zsl->length = 0;
    // 头节点层高为64(层高的最大限制)
    zsl->header = zslCreateNode(ZSKIPLIST_MAXLEVEL,0,NULL);
    for (j = 0; j < ZSKIPLIST_MAXLEVEL; j++) {
        zsl->header->level[j].forward = NULL;
        zsl->header->level[j].span = 0;
    }
    zsl->header->backward = NULL;
    zsl->tail = NULL;
    return zsl;
}

上述代码中可以看到，头节点的层高数组直接为最大长度，因为每次查找都要从头部开始，而且整个跳跃表的高度是动态增加的，初始化时直接按照最大值申请高度，避免后续高度增加时为头节点重新分配内存。所以之前的跳跃表图例应该如下图所示：

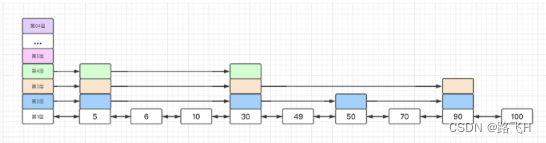
在这里插入图片描述

因为有backward指针的存在，所以第一层可以看作是一个双向链表。

插入节点

int zslRandomLevel(void) {
    // 计算当前插入元素层高的随机函数
    int level = 1;
    // (random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF) 概率为1/4
    while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF))
        level += 1;
    return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
}

zskiplistNode *zslInsert(zskiplist *zsl, double score, sds ele) {
    // update存放需要更新的节点
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    unsigned int rank[ZSKIPLIST_MAXLEVEL];
    int i, level;

    serverAssert(!isnan(score));
    x = zsl->header;
    // 第一步，收集需要更新的节点与步长信息
    for (i = zsl->level-1; i >= 0; i--) {
        /* store rank that is crossed to reach the insert position */
        rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];
        // score可以重复，重复时使用ele大小进行排序
        while (x->level[i].forward &&
                (x->level[i].forward->score < score ||
                    (x->level[i].forward->score == score &&
                    sdscmp(x->level[i].forward->ele,ele) < 0)))
        {
            rank[i] += x->level[i].span;
            x = x->level[i].forward;
        }
        update[i] = x;
    }
    // 第二步， 获取随机层高，补全需要更新的节点
    level = zslRandomLevel();
    if (level > zsl->level) {
        for (i = zsl->level; i < level; i++) {
            rank[i] = 0;
            update[i] = zsl->header;
            update[i]->level[i].span = zsl->length;
        }
        zsl->level = level;
    }
    // 第三步，创建并分层插入节点，同时更新同层前一节点步长信息
    x = zslCreateNode(level,score,ele);
    for (i = 0; i < level; i++) {
        x->level[i].forward = update[i]->level[i].forward;
        update[i]->level[i].forward = x;

        /* update span covered by update[i] as x is inserted here */
        x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);
        update[i]->level[i].span = (rank[0] - rank[i]) + 1;
    }
    // 第四步，更新新增节点未涉及层节点的步长信息，以及跳表相关信息
    /* increment span for untouched levels */
    for (i = level; i < zsl->level; i++) {
        update[i]->level[i].span++;
    }

    x->backward = (update[0] == zsl->header) ? NULL : update[0];
    if (x->level[0].forward)
        x->level[0].forward->backward = x;
    else
        zsl->tail = x;
    zsl->length++;
    return x;
}

插入节点分为四步(举个栗子，边吃边看)：

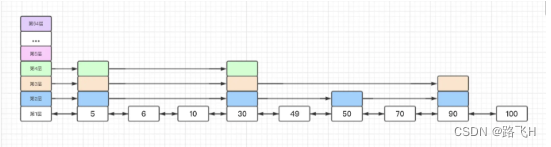
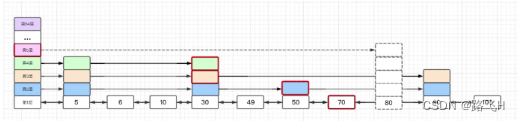
在这里插入图片描述

假设现在我需要插入元素80，且获取到随机的层高为5(为了所有情况都覆盖到)。

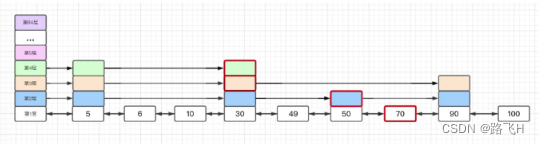
在这里插入图片描述

  1. 收集需要更新的节点与步长信息

    • 将插入新增节点后每层受影响节点存在update数组中，update[i]为第i + 1层会受影响节点(红框框出来的就是例子中可能会受影响的节点)。

    • 将每层头节点与会受影响的节点中间存在节点数存在rank数组中，rank[i]为头节点与第i + 1层会受影响节点中间存在的节点数(rank为[6, 5, 3, 3])。

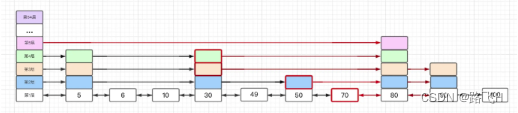
    在这里插入图片描述

  2. 获取随机层高，补全需要更新的节点，同时可能更新跳表高度

    • 通过zslRandomLevel函数计算当前插入节点侧层高，层高越高出现的几率越小(我们指定了是5，实际是随机的)。

    • 因为搜索需要更新节点是从跳跃表当前高度的那一层开始的，如果新插入的节点的层高比当前表高还高，那么高出的这几层的头节点也是需要更新信息的(第五层的头节点后继有人了，所以它也需要被更新)。

    • 如果当前层高高于表高，则更新表高(表高从4变成5)。

    在这里插入图片描述

  3. 创建并分层插入节点，同时更新同层前一节点步长信息

    • 创建节点，然后根据当前节点的层高，在每一层进行节点插入(和简单链表插入一样)。

    • 更新下每层前一个节点(update[i]对应节点)与自身节点的步长信息。

  4. 更新新增节点未涉及层节点的步长信息，以及跳表相关信息与节点自身的相关信息

    • 如果当前节点的层高比跳表高度低，那么高于当前节点层高的那些层中排在当前节点之后的节点步长信息都需要+1(因为在它和它的前一个节点之间插入了新元素)。

    • 更新跳表长度与当前节点与第一层下一节点的后退指针(后退指针可以理解为只有底层链表有)。

查找节点

/* Find the rank for an element by both score and key.
 * Returns 0 when the element cannot be found, rank otherwise.
 * Note that the rank is 1-based due to the span of zsl->header to the
 * first element. */
unsigned long zslGetRank(zskiplist *zsl, double score, sds ele) {
    zskiplistNode *x;
    unsigned long rank = 0;
    int i;

    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {
        while (x->level[i].forward &&
            (x->level[i].forward->score < score ||
                (x->level[i].forward->score == score &&
                sdscmp(x->level[i].forward->ele,ele) <= 0))) {
            rank += x->level[i].span;
            x = x->level[i].forward;
        }

        /* x might be equal to zsl->header, so test if obj is non-NULL */
        if (x->ele && sdscmp(x->ele,ele) == 0) {
            return rank;
        }
    }
    return 0;
}

/* Finds an element by its rank. The rank argument needs to be 1-based. */
zskiplistNode* zslGetElementByRank(zskiplist *zsl, unsigned long rank) {
    zskiplistNode *x;
    unsigned long traversed = 0;
    int i;

    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {
        while (x->level[i].forward && (traversed + x->level[i].span) <= rank)
        {
            traversed += x->level[i].span;
            x = x->level[i].forward;
        }
        if (traversed == rank) {
            return x;
        }
    }
    return NULL;
}

redis实现中跳跃表和dict共同实现了zset，dict实现O(1)复杂度获取元素对应score，跳跃表用来处理区间查询的相关操作，同时因为score可以重复，所以跳跃表无需实现通过ele获取score(通过dict查)以及通过score获取ele(貌似也没有这个需求)。

一般查询需求有两个：

  • 根据rank查询节点，主要是为了通过该节点指针进行遍历获取某个区间的节点数据。
  • 根据score与ele(score可能重复，所以需要ele)获取节点的rank,进行count之类的数值计算。

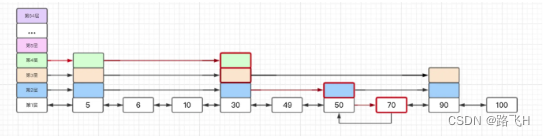
在这里插入图片描述

大体的流程都是按照从左上方开始向右下方搜索的路线进行查询(如上图红线标记路径)。

删除节点

/* Internal function used by zslDelete, zslDeleteByScore and zslDeleteByRank */
void zslDeleteNode(zskiplist *zsl, zskiplistNode *x, zskiplistNode **update) {
    int i;
    for (i = 0; i < zsl->level; i++) {
        // 被删除节点在第i层有节点，则update[i]为被删除节点的前一个节点
        if (update[i]->level[i].forward == x) {
            // 步长 = 原步长 + 被删除节点步长 - 1（被删除节点）
            update[i]->level[i].span += x->level[i].span - 1;
            // 指针越过被删除节点
            update[i]->level[i].forward = x->level[i].forward;
        } else {
            // 被删除节点在第i层无节点，则 步长 = 原步长 - 1(被删除节点)
            update[i]->level[i].span -= 1;
        }
    }
    if (x->level[0].forward) {
        // 更新被删除节点下一节点的后退指针
        x->level[0].forward->backward = x->backward;
    } else {
        zsl->tail = x->backward;
    }
    while(zsl->level > 1 && zsl->header->level[zsl->level-1].forward == NULL)
        zsl->level--;
    zsl->length--;
}

int zslDelete(zskiplist *zsl, double score, sds ele, zskiplistNode **node) {
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    int i;

    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {
        while (x->level[i].forward &&
                (x->level[i].forward->score < score ||
                    (x->level[i].forward->score == score &&
                     sdscmp(x->level[i].forward->ele,ele) < 0)))
        {
            x = x->level[i].forward;
        }
        update[i] = x;
    }
    /* We may have multiple elements with the same score, what we need
     * is to find the element with both the right score and object. */
    x = x->level[0].forward;
    if (x && score == x->score && sdscmp(x->ele,ele) == 0) {
        zslDeleteNode(zsl, x, update);
        if (!node)
            zslFreeNode(x);
        else
            *node = x;
        return 1;
    }
    return 0; /* not found */
}

删除节点与添加节点步骤类似，分为三步：

  1. 收集需要更新的节点。
  2. 删除节点所在的层链表移除节点(和简单链表移除节点一样)，并更新前一节点的步长信息(update[i]所存节点)。
  3. 更新跳跃表高度与长度。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1146362.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

LED主流光源-高均匀条形光源

LED主流光源-高均匀条形光源

&#xff08;1&#xff09;产品特点&#xff1a; ① 高均匀条形照明光源&#xff0c;可制作长度最长为 2000mm 的光源&#xff1b; ② 可用 M3 螺纹孔安装&#xff0c;也可以在三个挤型槽内插入 M3 螺母安装。 &#xff08;2&#xff09;应用领域&#xff1a; ① 电子元件识别与…
阅读更多...
掌握Python：开启未来的大门

掌握Python：开启未来的大门

Python&#xff0c;一门以其简洁性和多才多艺而著称的编程语言&#xff0c;正成为未来的关键技能之一。随着数字时代的到来&#xff0c;Python的发展前景愈发广泛&#xff0c;而且其易学性吸引着越来越多的学习者。 1.Python的发展前景&#xff1a; Python在数据科学、人工智能…
阅读更多...
任正非说：我们要改善和媒体的关系，而不是要利用媒体，不要自以为聪明。

任正非说：我们要改善和媒体的关系，而不是要利用媒体，不要自以为聪明。

嗨&#xff0c;你好&#xff01;这是华研荟【任正非说】系列的第22篇文章&#xff0c;让我们继续聆听任正非先生的真知灼见&#xff0c;学习华为的管理思想和管理理念。 一、我曾经在与一个世界著名公司&#xff0c;也是我司全方位的竞争对手的合作时讲过&#xff0c;我是拉宾的…
阅读更多...
【数学基础】【进制转换】十进制转其他进制、其他进制转十进制

【数学基础】【进制转换】十进制转其他进制、其他进制转十进制

十进制转其他进制 JavaScript实现 const convert (num,base2)>{return !num?0:convert(~~(num/base),base)*10(num%base); } convert(8,2) // 1000 convert(8,8) // 10 convert(8,16) // 8其他进制转十进制 JavaScript实现 const reconvert (num,base2,curr1)>{retu…
阅读更多...
代码随想录算法训练营第4天| 24. 两两交换链表中的节点、19.删除链表的倒数第N个节点、面试题 02.07. 链表相交 、142.环形链表II

代码随想录算法训练营第4天| 24. 两两交换链表中的节点、19.删除链表的倒数第N个节点、面试题 02.07. 链表相交 、142.环形链表II

JAVA语言编写 24. 两两交换链表中的节点 谷歌、亚马逊、字节、奥多比、百度 给你一个链表&#xff0c;两两交换其中相邻的节点&#xff0c;并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题&#xff08;即&#xff0c;只能进行节点交换&#xff09;。…
阅读更多...
浙大网新：重视AI驱动，就是重视未来发展

浙大网新：重视AI驱动，就是重视未来发展

【科技明说 &#xff5c; 重磅专题】 对于浙大网新在AI方面的发展情况&#xff0c;我是看到一个消息之后才开始有了关注&#xff0c;之前总感觉浙大网新在AI方面战略雷声大雨点小&#xff0c;然而当我看到这个消息后才发现&#xff0c;浙大网新其实也非常重视AI方面的发展。 …
阅读更多...
【微信小程序】WXML的模板语法与WXSS模板样式

【微信小程序】WXML的模板语法与WXSS模板样式

&#x1f5a5;️&#x1f5a5;️&#x1f5a5;️ 博主主页&#xff1a; &#x1f449;&#x1f3fb; &#x1f449;&#x1f3fb; &#x1f449;&#x1f3fb; 糖 &#xff0d;O&#xff0d; &#x1f6a9;&#x1f6a9;&#x1f6a9;微信小程序专栏&#xff1a;微信小程序 &…
阅读更多...
聚量推客升级啦，加入了外卖cps、话费充值等

聚量推客升级啦，加入了外卖cps、话费充值等

“聚量推客”升级啦&#xff0c;加入了生活cps模块&#xff0c;包含美团外卖cps、滴滴打车出行cps、电影票推广、话费充值等cps推广场景&#xff0c;聚量推客不止是app地推拉新和网推拉新平台&#xff0c;更是一个 综合性推广平台&#xff0c;未来会接入越来越多的推广场景&…
阅读更多...
OpenCV官方教程中文版 —— Hough 直线变换

OpenCV官方教程中文版 —— Hough 直线变换

OpenCV官方教程中文版 —— Hough 直线变换 前言一、原理二、OpenCV 中的霍夫变换三、Probabilistic Hough Transform 前言 目标 • 理解霍夫变换的概念 • 学习如何在一张图片中检测直线 • 学习函数&#xff1a;cv2.HoughLines()&#xff0c;cv2.HoughLinesP() 一、原理…
阅读更多...
基础课13——数据异常处理

基础课13——数据异常处理

数据异常是指数据不符合预期或不符合常识的情况。数据异常可能会导致数据分析结果不准确&#xff0c;甚至是错误&#xff0c;因此在进行数据分析之前需要对数据进行清洗和验证。 常见的数据异常包括缺失值、重复值、异常值等。 缺失值是指数据中存在未知值或未定义的值&#…
阅读更多...
Winform 多语言化快速解析替换工具-1分钟一个界面

Winform 多语言化快速解析替换工具-1分钟一个界面

随着业务的扩展&#xff0c;有的软件有多语言化的需求。那么如果软件已经很多写死的文字内容如何快速进行语言化替换呢&#xff0c;一个一个去改工作量太大。 于是开发了个小工具用来替换现有内容并生成语音包&#xff0c;原理就是采用正则表达式进行匹配控件关键字以及中文进…
阅读更多...
使用MLC-LLM将RWKV 3B模型跑在Android手机上

使用MLC-LLM将RWKV 3B模型跑在Android手机上

0x0. 前言 这篇文章主要是填一下 MLC-LLM 部署RWKV World系列模型实战&#xff08;3B模型Mac M2解码可达26tokens/s&#xff09; 这里留下来的坑&#xff0c;这篇文章里面介绍了如何使用 MLC-LLM 在A100/Mac M2上部署 RWKV 模型。但是探索在Android端部署一个RWKV对话模型的ap…
阅读更多...
宇信科技：强势行业加速融入AIGC，同时做深做细

宇信科技：强势行业加速融入AIGC，同时做深做细

【科技明说 &#xff5c; 重磅专题】 大家可能没有想到&#xff0c;一向对外低调行事的宇信科技&#xff0c;在AIGC方面2023年就已经训练出了适配金融场景的垂直模型&#xff0c;并应用到了各产品线上&#xff0c;同时结合通用大模型预研了宇信金融系统编程大模型。宇信金融系…
阅读更多...
IOC课程整理-15 Spring 类型转换

IOC课程整理-15 Spring 类型转换

1. Spring 类型转换的实现 2. 使用场景 3. 基于 JavaBeans 接口的类型转换 4. Spring 內建 PropertyEditor 扩展 5. 自定义 PropertyEditor 扩展 6. Spring PropertyEditor 的设计缺陷 7. Spring 3 通用类型转换接口 8. Spring 內建类型转换器 9. Converter 接口的局限性 10. G…
阅读更多...
Azure - 机器学习：使用 Apache Spark 进行交互式数据整理

Azure - 机器学习：使用 Apache Spark 进行交互式数据整理

目录 本文内容先决条件使用 Apache Spark 进行交互式数据整理Azure 机器学习笔记本中的无服务器 Spark 计算从 Azure Data Lake Storage (ADLS) Gen 2 导入和整理数据从 Azure Blob 存储导入和处理数据从 Azure 机器学习数据存储导入和整理数据 关注TechLead&#xff0c;分享AI…
阅读更多...
深入理解Linux网络笔记（五）：深度理解本机网络IO

深入理解Linux网络笔记（五）：深度理解本机网络IO

本文为《深入理解Linux网络》学习笔记&#xff0c;使用的Linux源码版本是3.10&#xff0c;网卡驱动默认采用的都是Intel的igb网卡驱动 Linux源码在线阅读&#xff1a;https://elixir.bootlin.com/linux/v3.10/source 4、深度理解本机网络IO 1&#xff09;、跨机网络通信过程 …
阅读更多...
快速排序——及其改进

快速排序——及其改进

hoare版本&#xff08;原始版本&#xff09;&#xff1a; 思想&#xff1a;树的遍历思想&#xff0c;先把数组第一个数作为KEY,然后left从左到右&#xff0c;right从右到左一起走&#xff0c;当left找到比key大的值时停下来&#xff0c;当right找到比key小的值时停下来&#xf…
阅读更多...
通讯网关软件030——利用CommGate X2Modbus实现Modbus RTU访问Mysql服务器

通讯网关软件030——利用CommGate X2Modbus实现Modbus RTU访问Mysql服务器

本文介绍利用CommGate X2Modbus实现Modbus RTU访问Mysql数据库。CommGate X2MODBUS是宁波科安网信开发的网关软件&#xff0c;软件可以登录到网信智汇(http://wangxinzhihui.com)下载。 【案例】如下图所示&#xff0c;实现上位机通过Modbus RTU来获取Mysql数据库的数据。 【解…
阅读更多...
IOC课程整理-16

IOC课程整理-16

1. Java 泛型基础 Java中的泛型擦除&#xff08;Type Erasure&#xff09;是Java编译器为了兼容之前的非泛型代码而采用的一种机制。在编译过程中&#xff0c;Java编译器会将泛型类型转换为原始类型&#xff0c;并在必要时插入强制类型转换。 泛型擦除有以下几个主要特点&…
阅读更多...
深度学习_1 介绍；安装环境

深度学习_1 介绍；安装环境

深度学习 学习自李沐老师的课程。笔记主要以总结老师所讲解的内容以及我个人的想法为主&#xff0c;侵删&#xff01; 课程链接&#xff1a;课程安排 - 动手学深度学习课程 (d2l.ai) 介绍 AI地图&#xff1a; 我们以前写的非 AI 类程序基本都是人自己去想会遇到什么样的问题…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023