文章目录
- 二次函数
- 1.1 二次函数
- 1.2 二次函数的图像
- 1.2.1 a > 0 时
- 1.2.2 a < 0 时
- 1.2.3 二次函数的平移
- 1.2.4 普通二次型函数图像总结
- 1.3 其他形式的二次函数
- 1.3.1 顶点式
- 1.3.2 交点式
- 1.4 二次函数与直线的交点
二次函数
1.1 二次函数
二次函数的定义:y = ax2 + bx + c(其中 a ≠ 0 ,b和c没有要求)
二次函数的性质:
- 连续性
- 可导性
- 奇偶性
- 单调性
1.2 二次函数的图像
1.2.1 a > 0 时
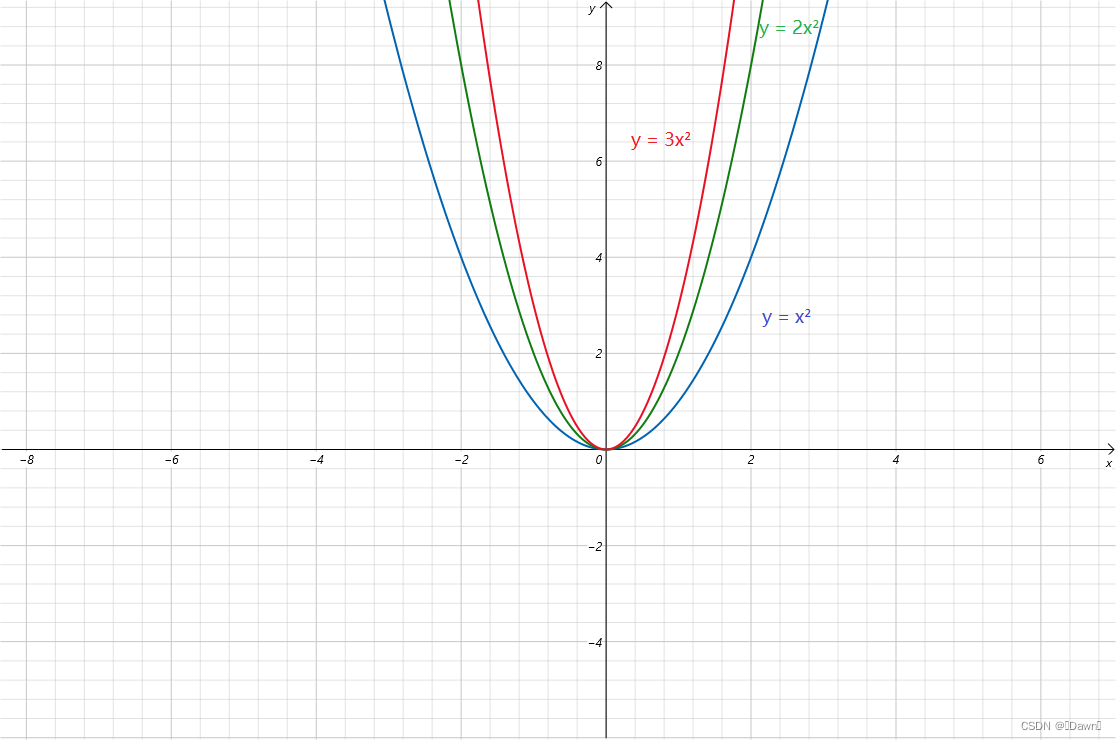
由上图可知:
- 顶点:都为(0,0)
- 对称轴:都为 y轴(x = 0)
- 奇偶性:都为 偶函数
- 单调性:y轴的左侧都为单调递减,y轴的右侧都为单调递增
- 开口大小:|a|越大,开口越小;|a|越小,开口越大
1.2.2 a < 0 时
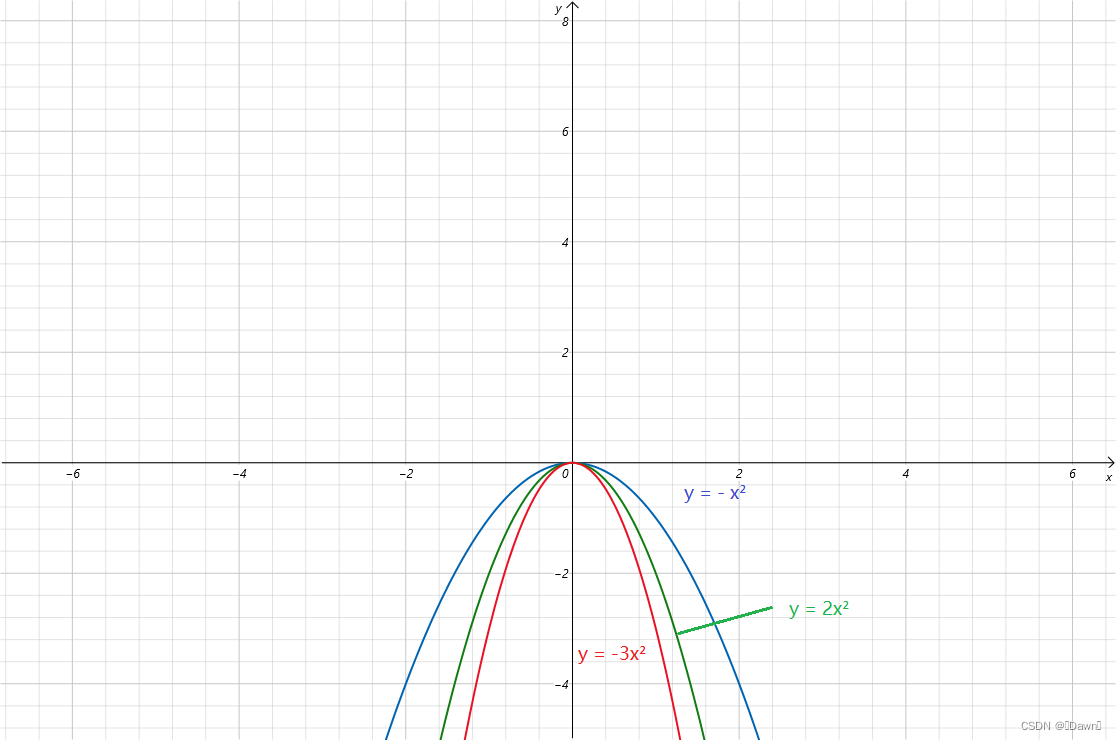
由上图可知:
- 顶点:都为(0,0)
- 对称轴:都为 y轴(x = 0)
- 奇偶性:都为 偶函数
- 单调性:y轴的左侧都为单调递增,y轴的右侧都为单调递减
- 开口大小:|a|越大,开口越小;|a|越小,开口越大
1.2.3 二次函数的平移
对x(沿x轴移动):左加,右减
- y = x2,y = (x + 1)2,y = (x -3)2 的图像如下所示:
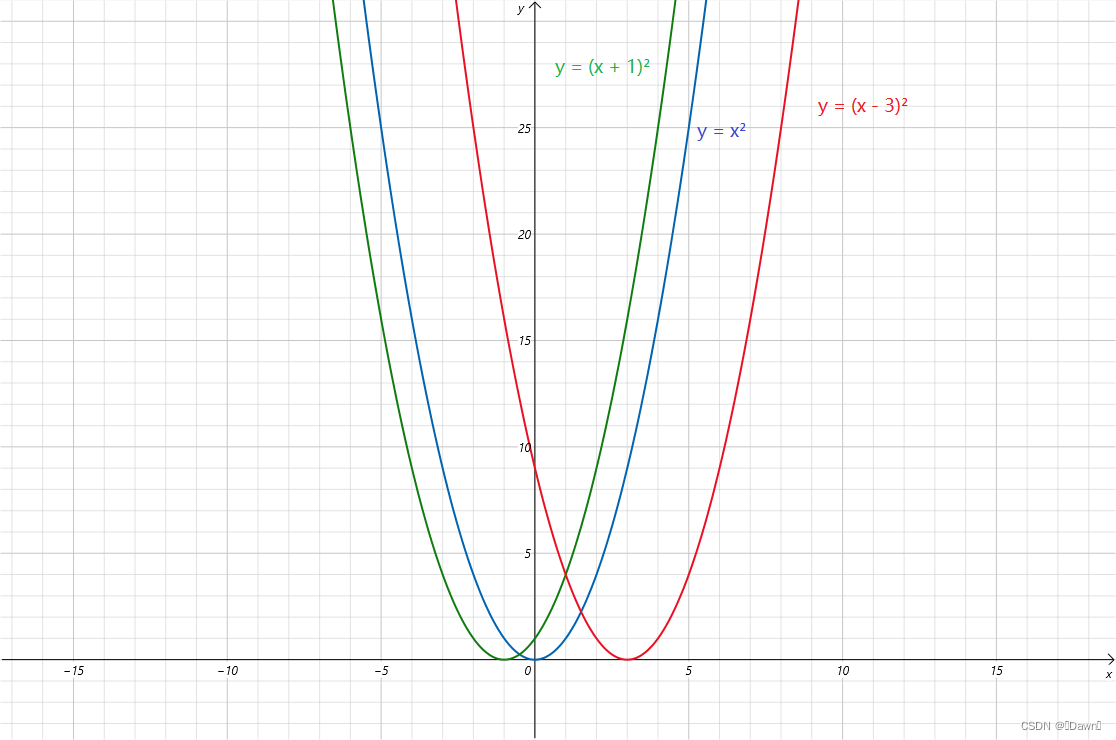
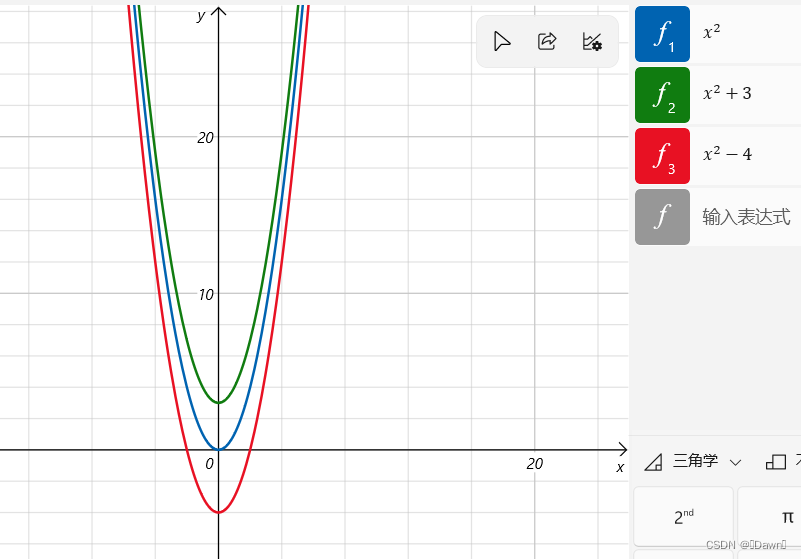
对y(沿y轴移动):上加,下减
- y = x2,y = x2 + 3,y = x2 - 4 的图像如下所示:
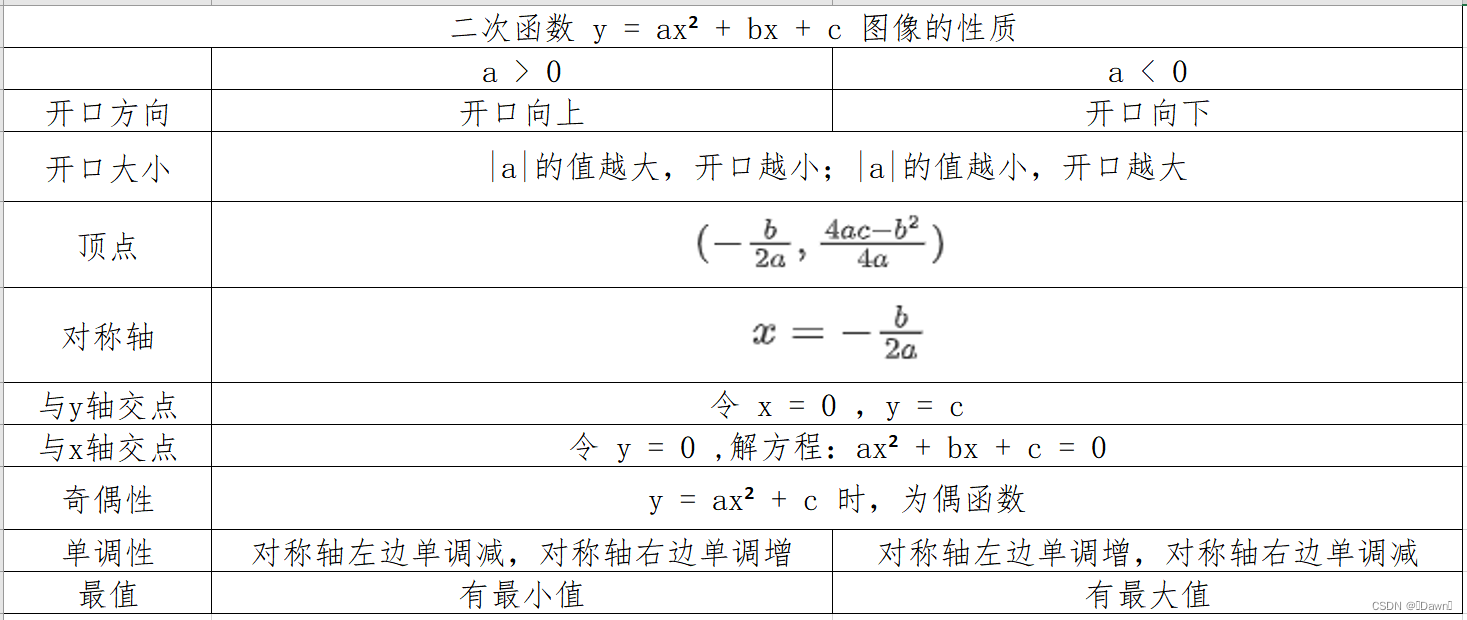
1.2.4 普通二次型函数图像总结
1.3 其他形式的二次函数
1.3.1 顶点式
二次函数的顶点式形式:y = a(x - h)² + k (a ≠ 0,a、h、k为常数)
顶点:(h,k)对称轴:x = h- 开口方向:a > 0,开口向上;a < 0,开口向下
1.3.2 交点式
二次函数的交点式形式:y=a(x - x1)(x - x2)(a ≠ 0,x1、x2为常数)。未必所有的二次函数都可以化为交点式
与x轴交点:(x1, 0),(x2, 0)
开口方向:a > 0,开口向上;a < 0,开口向下
对称轴: x = x 1 + x 2 2 x = \frac{x_1 + x_2}{2} x=2x1+x2
1.4 二次函数与直线的交点
二次函数 y = ax2 + bx + c 与 直线 y = kx + m :
- 二式联立得:ax2 + bx + c = kx + m
- 解方程:ax2 + (b - k)x + c-m = 0
- 判别式:Δ = (b - k)2 - 4a(c-m)
1.Δ < 0,没有交点
2.Δ = 0,有一个交点
3.Δ > 0,有两个交点