题目：

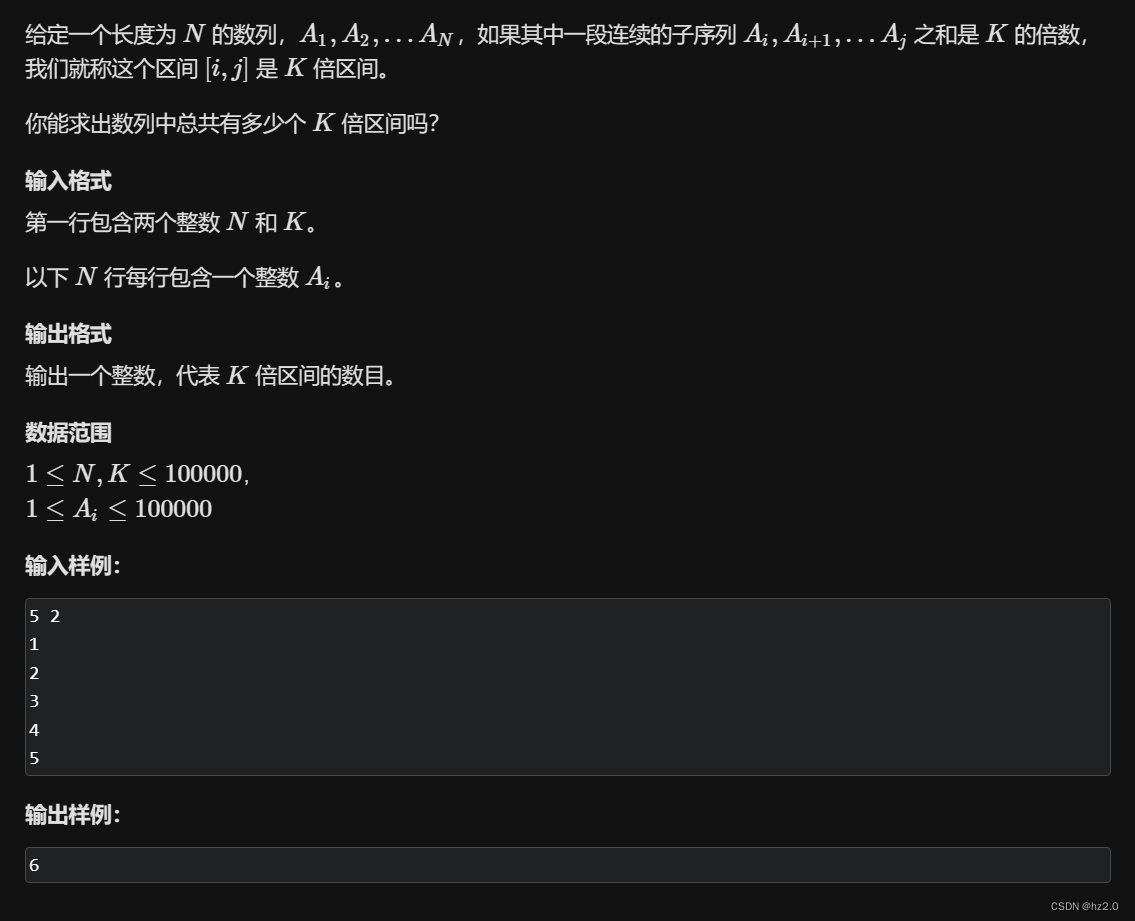
1230. K倍区间 - AcWing题库

突破口：

区间遍历枚举一般先枚举右端点，再枚举左端点，注意由右端点限制左端点

思路：1.暴力

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<string>
using namespace std;
typedef unsigned long long ull;
const int N = 100010;
ull s[N];//既是用来存储原数据的，也是用来存储前缀和的
ull n, k,ans;

/*区间遍历枚举一般先枚举右端点，再枚举左端点，注意由右端点限制左端点*/

int main()
{
    cin >> n >> k;
    
    //法一：暴力(时间复杂度：O(n3))
    for (int i = 1; i <= n; i++) scanf("%d", &s[i]);
    

    for(int r=1;r<=n;r++)
        for (int l = 1; l <= r; l++) {
            int sum = 0;
            for (int i = l; i <= r; i++)sum += s[i];
            if (sum % k == 0)ans++;
        }
    cout << ans;
}

思路二：前缀和

#include<string>
using namespace std;
typedef unsigned long long ull;
const int N = 100010;
ull s[N];//既是用来存储原数据的，也是用来存储前缀和的
ull n, k,ans;

/*区间遍历枚举一般先枚举右端点，再枚举左端点，注意由右端点限制左端点*/

int main()
{
    cin >> n >> k;
    //法二：前缀和（时间复杂度：O(n2)）
    for (int i = 1; i <= n; i++) {
        scanf("%d", &s[i]);
        s[i] += s[i - 1];//前缀和
    }

    for (int r = 1; r <= n; r++) {
        for (int l = 1; l <= r; l++) {
            if ((s[r] - s[l - 1]) % k == 0)ans++;
        }
    }
    cout << ans;
}

思路三：在前缀和基础上优化

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<string>
using namespace std;
typedef unsigned long long ull;
const int N = 100010;
ull s[N];//既是用来存储原数据的，也是用来存储前缀和的
ull n, k,ans;
ull cnt[N]; // 用云存储余数为s[i] % k的数有多少个
/*区间遍历枚举一般先枚举右端点，再枚举左端点，注意由右端点限制左端点*/

int main()
{
    cin >> n >> k;

    /*法三：前缀和优化（数论）（时间复杂度：O(n)）----以空间换时间
           对于for (int l = 1; l <= r; l++) 
                if ((s[r] - s[l - 1]) % k == 0)ans++;
           这是求在0~r-1的范围内有多少个s[l]可以满足(s[r] - s[l - 1]) % k == 0-->
           其等价于求在右端点r之前余数为s[r]%k的数有多少个
           定义cnt[N],用云存储余数为s[i]%k的数有多少个*/
    
    for (int i = 1; i <= n; i++) {
        scanf("%d", &s[i]);
        s[i] += s[i - 1];//前缀和
    }

    for (int r = 0; r <= n; r++) {
        ans += cnt[s[r] % k];
        cnt[s[r] % k]++;
    }
    cout << ans;
}