AcWing 1.2.1 最长上升子序列模型 + 动态规划 + 图解（详细）

news2024/11/18 9:36:08

（1）acwing 4557. 最长上升子序列 4557. 最长上升子序列 - AcWing题库

给定一个长度为 N 的整数序列 a1,a2,…,aN。请你计算该序列的最长上升子序列的长度。上升子序列是指数值严格单调递增的子序列

输入格式
  • 第一行包含整数 N
  • 第二行包含 N个整数 a1,a2,…,aN
输出格式
  • 一行，一个整数，表示最长上升子序列的长度
数据范围
  • 1≤N≤1000
  • 0≤ai≤100000
输入样例：
7
1 7 3 5 9 4 8
输出样例：
4

 C++代码：

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 1010;

int n,res=0;
int arr[N],dp[N];

int main() {
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d",&arr[i]);
    for(int i=1;i<=n;i++) {
        dp[i]=1;
        for(int j=1;j<i;j++) {
            if(arr[j]<arr[i]) 
                dp[i] = max(dp[i],dp[j]+1);
        }
        if (res < dp[i]) res = dp[i]; // 取长的子序列
    }
    printf("%d\n",res);
    return 0;
}

也可以这样写：

int main() {
    scanf("%d",&n);
    for(int i=0;i<n;i++) scanf("%d",&arr[i]);
    dp[0]=1;
    for(int i=1;i<n;i++) {
        dp[i]=1;
        for(int j=0;j<i;j++) {
            if(arr[j]<arr[i]) 
                dp[i] = max(dp[i],dp[j]+1);
        }
        if (res < dp[i]) res = dp[i]; // 取长的子序列
    }
    printf("%d\n",res);
    return 0;
}

======================================================

int main() {
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d",&arr[i]);
    dp[1]=1;
    for(int i=2;i<=n;i++) {
        dp[i]=1;
        for(int j=1;j<i;j++) {
            if(arr[j]<arr[i]) 
                dp[i] = max(dp[i],dp[j]+1);
        }
        if (res < dp[i]) res = dp[i]; // 取长的子序列
    }
    printf("%d\n",res);
    return 0;
}

（2）acwing1017-怪盗基德的滑翔翼

假设城市中一共有 N幢 建筑排成一条线，每幢建筑的高度各不相同。初始时，怪盗基德可以在任何一幢建筑的顶端。他可以选择一个方向逃跑，但是不能中途改变方向（因为中森警部会在后面追击）。因为滑翔翼动力装置受损，他只能往下滑行（即：只能从较高的建筑滑翔到较低的建筑）。他希望尽可能多地经过不同建筑的顶部，这样可以减缓下降时的冲击力，减少受伤的可能性。请问，他最多可以经过多少幢不同建筑的顶部(包含初始时的建筑)？

输入格式

  • 输入数据第一行是一个整数K，代表有K组测试数据
  • 每组测试数据包含两行：第一行是一个整数N，代表有N幢建筑。第二行包含N个不同的整数，每一个对应一幢建筑的高度h，按照建筑的排列顺序给出

输出格式

  • 对于每一组测试数据，输出一行，包含一个整数，代表怪盗基德最多可以经过的建筑数量

数据范围

  • 1≤K≤100,
  • 1≤N≤100,
  • 0<h<10000

输入样例：

3
8
300 207 155 299 298 170 158 65
8
65 158 170 298 299 155 207 300
10
2 1 3 4 5 6 7 8 9 10

输出样例：

6
6
9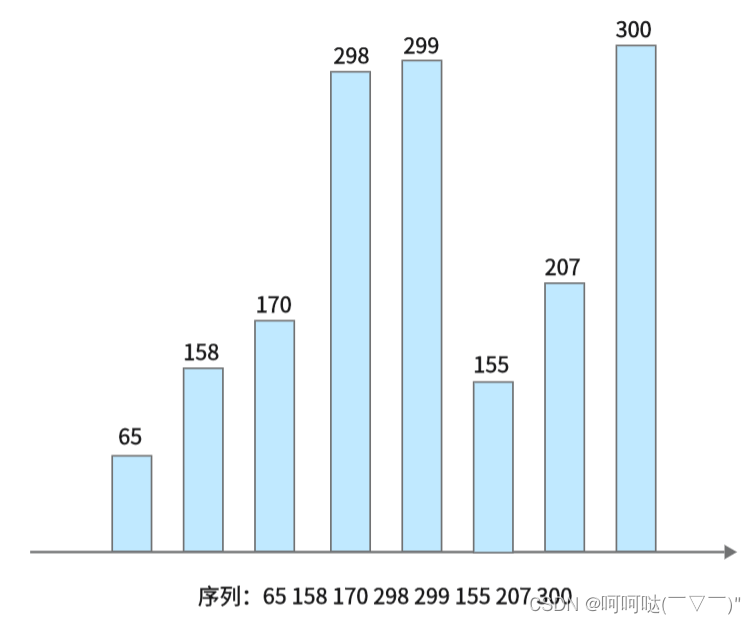

思路：移动方向一旦确定，就转换成了LIS问题，那么可以看作是两个方向的最长上升子序列问题，答案res为正向和逆向LIS两个过程中的较大者。

 C++代码：

// 当确定完方向和起点后，最长的距离是什么呢？
// 起点：a[i]
// 最长距离：以a[i]为结尾的最长上升子序列

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;

int n;
int arr[N],dp[N];

int main() {
	int T;
	scanf_s("%d", &T);
	while (T--) {
		scanf_s("%d", &n);
		for (int i = 1; i <= n; i++) scanf_s("%d", &arr[i]);
		// 正向求解LIS问题
		int res = 0;
		for (int i = 1; i <= n; i++) {
			dp[i] = 1;
			for (int j = 1; j < i; j++) {
				if (arr[i] > arr[j]) dp[i] = max(dp[i], dp[j] + 1);
			}
			res = max(res, dp[i]);
		}
		// 反向求解LIS问题
		for (int i = n; i>=1; i--) {
			dp[i] = 1;
			for (int j = n; j > i; j--) {
				if (arr[i] > arr[j]) dp[i] = max(dp[i], dp[j] + 1);
			}
			res = max(res, dp[i]);
		}
		printf("%d\n", res);
	}
	return 0;
}

（3）acwing1014-登山问题

五一到了，ACM队 组织大家去登山观光，队员们发现山上一共有N个景点，并且决定按照顺序来浏览这些景点，即每次所浏览景点的编号都要大于前一个浏览景点的编号。同时队员们还有另一个登山习惯，就是不连续浏览海拔相同的两个景点，并且一旦开始下山，就不再向上走了。队员们希望在满足上面条件的同时，尽可能多的浏览景点，你能帮他们找出最多可能浏览的景点数么？

输入格式

  • 第一行包含整数N，表示景点数量
  • 第二行包含N个整数，表示每个景点的海拔

输出格式

  • 输出一个整数，表示最多能浏览的景点数

数据范围

  • 2≤N≤1000

输入样例

8
186 186 150 200 160 130 197 220

输出样例

4

本题实质上是求正向和反向两次LIS问题，两次的LIS过程相互独立，故所求为两端LIS过程中最长上升子序列的最大长度之和

  • res = max(res,f[i]+g[i]-1)

C++代码：

/*
	条件1：按照编号递增的顺序来浏览 => 必须是子序列
	条件2：相邻两个景点不能相同
	条件3：一旦开始下降，就不能上升了

	目标：求最多能浏览多少景点
*/

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 1010;

int n;
int arr[N];
int f[N], g[N];

int main() {
	scanf_s("%d", &n);
	for (int i = 1; i <= n; i++) scanf_s("%d", &arr[i]);
	for (int i = 1; i <= n; i++) {
		f[i] = 1;
		for (int j = 1; j < i; j++) {
			if (arr[i] > arr[j]) f[i] = max(f[i], f[j] + 1);
		}
	}
	for (int i = n; i >= 1; i--) {
		g[i] = 1;
		for (int j = n; j > i; j--) {
			if (arr[i] > arr[j]) g[i] = max(g[i], g[j] + 1);
		}
	}
	int res = 0;
	for (int i = 1; i <= n; i++) res = max(res, f[i] + g[i] - 1);
	printf("%d\n", res);
	return 0;
}

（4）acwing 482.合唱队形 482. 合唱队形 - AcWing题库

N 位同学站成一排，音乐老师要请其中的 (N−K) 位同学出列，使得剩下的 K 位同学排成合唱队形。合唱队形是指这样的一种队形：设 K 位同学从左到右依次编号为 1，2…，K 他们的身高分别为 T1，T2，…，TK 则他们的身高满足 T1<…<Ti>Ti+1>…>TK(1≤i≤K)。你的任务是，已知所有 N 位同学的身高，计算最少需要几位同学出列，可以使得剩下的同学排成合唱队形。

输入格式
  • 输入的第一行是一个整数 N ，表示同学的总数
  • 第二行有 N 个整数，用空格分隔，第 i  个整数 Ti  是第 i 位同学的身高(厘米)
输出格式
  • 输出包括一行，这一行只包含一个整数，就是最少需要几位同学出列
数据范围
  • 2≤N≤100
  • 130≤T≤230

思路： 如果要使得出列的同学数量最少的话，就意味着要使剩下的数量最多。那意思就是要找到一个先上升再下降的序列，选个最大的。然后再用总数减去这个长度。

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 1010;

int n;
int arr[N];
int f[N],g[N];

int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) scanf("%d", &arr[i]);
    for(int i=1;i<=n;i++) {
        f[i] = 1;
        for(int j=1;j<i;j++) {
            if(arr[i]>arr[j]) f[i] = max(f[i], f[j] + 1);
        }
    }
    for(int i=n;i>=1;i--) {
        g[i] = 1;
        for(int j=n;j>i;j--) {
            if(arr[i]>arr[j]) g[i] = max(g[i], g[j] + 1);
        }
    }
    int res=0;
    for(int i=1;i<=n;i++) res = max(res,f[i]+g[i]-1);
    printf("%d",n-res);
    return 0;
}

（5）acwing 1012.友好城市

输入样例： 

7
22 4
2 6
10 3
15 12
9 8
17 17
4 2

输出样例： 

4

 

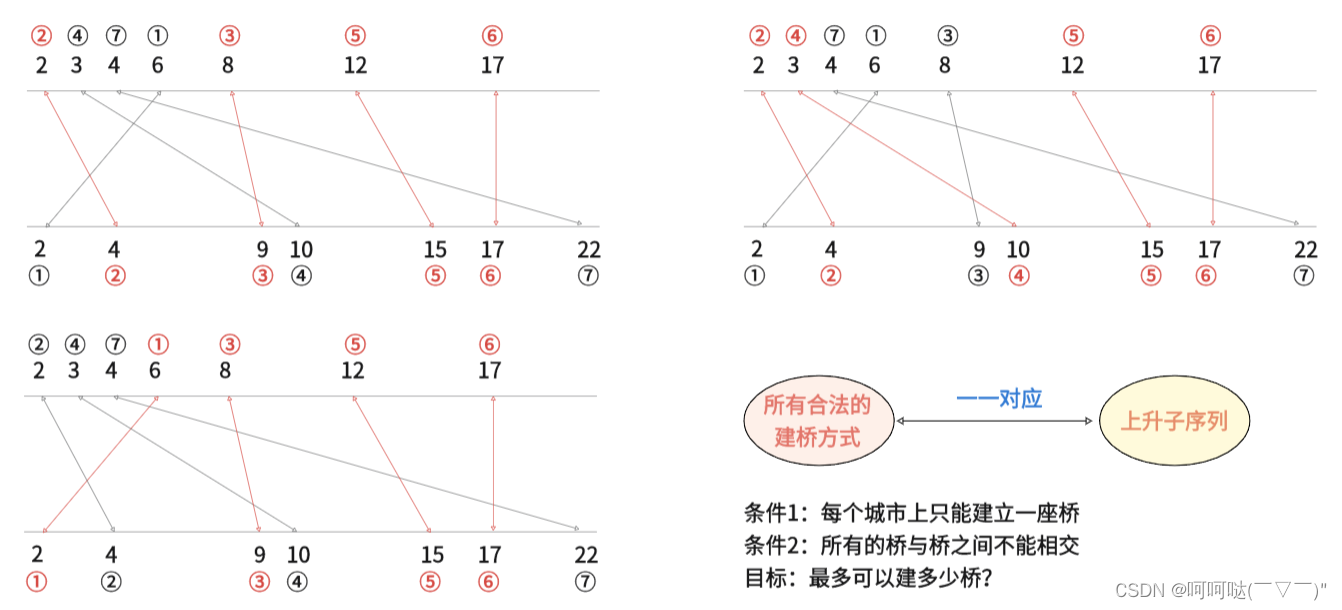
>>思路和分析

对于任意一种合法的建立桥梁的方式，都可以对应一种因变量的上升子序列。反之，对于因变量的任何一个上升子序列，我们都可以唯一的对应一个合法的建桥方式。每一种建桥方式，建桥的数量和上升子序列的长度是相同的。因此左边集合（所有合法的建桥方式）的长度最大值就等于右边集合（上升子序列）的长度的最大值。
解法：先按照自变量的大小，把因变量排序。排好之后得到一个序列，然后在序列当中求最长的一个上升子序列。
排序思路：看一下什么会出现相交的情况？
本质：如果选出来的桥梁是没有交叉的，那么就意味着按照其中某一个点来排序，那么另外一个点对应的位置也一定要使有序的才可以。因为一旦出现逆序，就是有交叉的。没有交叉也就意味着一定没有逆序的。那本题其实就可以转化为求最长上升子序列的长度。 

C++代码： 

#include <iostream>
#include <algorithm>

using namespace std;

typedef pair<int, int> PII;

const int N = 5010;

int n;
PII q[N];
int f[N];

int main() {
	scanf_s("%d", &n);
	for (int i = 0; i < n; i++) scanf_s("%d%d", &q[i].first, &q[i].second);
	sort(q, q + n);

	int res = 0;
	for (int i = 0; i < n; i++) {
		f[i] = 1;
		for (int j = 0; j < i; j++) {
			if (q[i].second > q[j].second) f[i] = max(f[i], f[j] + 1);
		}
		res = max(res, f[i]);
	}
	printf("%d\n",res);
	return 0;
}

（6）acwing 1016.最长上升子序列和

输入样例：  

7
1 7 3 5 9 4 8

 输出样例： 

18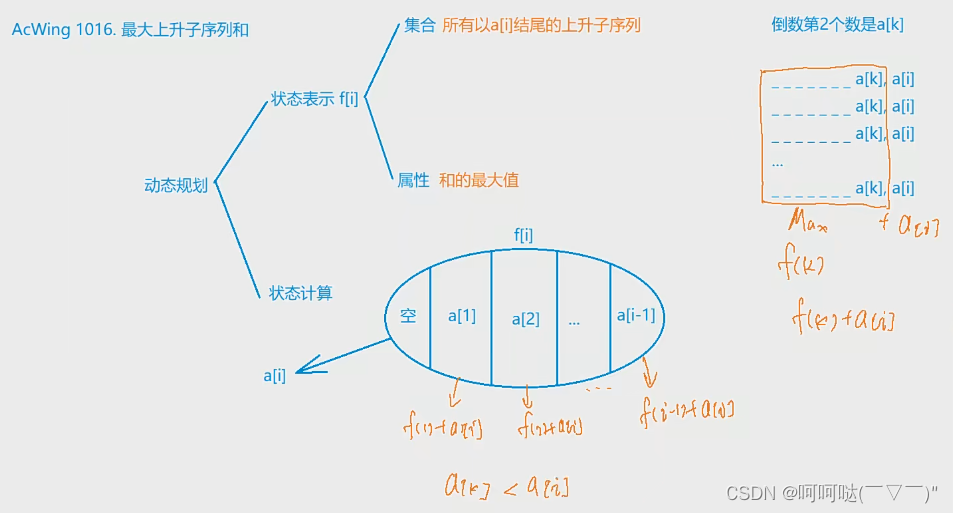

 C++代码：

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;
int n;
int a[N], f[N];

int main() {
	scanf_s("%d", &n);
	for (int i = 1; i <= n; i++) scanf_s("%d", &a[i]);
	for (int i = 1; i <= n; i++) {
		f[i] = a[i];
		for (int j = 1; j <i; j++) {
			if (a[i] > a[j]) f[i] = max(f[i], f[j] + a[i]);
		}
	}
	int res = 0;
	for (int i = 1; i <= n; i++) res = max(res, f[i]);
	printf("%d\n", res);
	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1142208.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

LLM系列 | 23：多模态大模型：浦语·灵笔InternLM-XComposer解读、实战和思考

LLM系列 | 23：多模态大模型：浦语·灵笔InternLM-XComposer解读、实战和思考

引言 ​简介 模型解读 模型架构 训练 实战 环境准备 本地实测 服务部署 总结 引言 谁念西风独自凉&#xff0c;萧萧黄叶闭疏窗&#xff0c;沉思往事立残阳。 Created by DALLE 3 小伙伴们好&#xff0c;我是《小窗幽记机器学习》的小编&#xff1a;卖热干面的小女孩…
阅读更多...
在Golang中理解错误处理

在Golang中理解错误处理

处理Golang中临时错误和最终错误的策略和示例 作为一名精通Golang的开发人员&#xff0c;您了解有效的错误处理是编写健壮可靠软件的关键因素。在复杂系统中&#xff0c;错误可能采取各种形式&#xff0c;包括临时故障和最终失败。在本文中&#xff0c;我们将探讨处理Golang中…
阅读更多...
源码解析SpringMVC之RequestMapping注解原理

源码解析SpringMVC之RequestMapping注解原理

1、启动初始化 核心&#xff1a;得到应用上下文中存在的全部bean后依次遍历&#xff0c;分析每一个目标handler & 目标方法存在的注解RequestMapping&#xff0c;将其相关属性封装为实例RequestMappingInfo。最终将 uri & handler 之间的映射关系维护在类AbstractHand…
阅读更多...
Java入门篇 之 数据类型（简单介绍）

Java入门篇 之 数据类型（简单介绍）

博主回归学习状态的第三篇文章&#xff0c;希望对大家有所帮助 今日份励志文案:你若决定灿烂&#xff0c;山无遮&#xff0c;海无拦 加油&#xff01; Java中一共存在2种数据类型 1 . 基本数据类型,基本数据类型四种和八种之说(具体看下图) 四种说的是&#xff0c;整数型&…
阅读更多...
vscode打开settings.json方法

vscode打开settings.json方法

cmd shift p&#xff0c;输入setting Open Workspace Settings 也会打开UI设置界面&#xff1b; Open User Settings (JSON) 会打开用户设置 settings.json 文件&#xff1b; Open Workspace Settings (JSON) 会打开工作区设置 settings.json 文件 vscode存在两种设置 sett…
阅读更多...
损失函数和目标函数|知识补充

损失函数和目标函数|知识补充

这张图中&#xff0c;横坐标size表示房屋的大小&#xff0c;纵坐标price表示房屋的价格&#xff0c;现在需要建立模型来表示两者之间的关系。 对于给定的输入x&#xff0c;模型会有一个输出f(x)&#xff0c;用一个函数来度量拟合的程度&#xff0c;也就是真实值和预测值之间的…
阅读更多...
前端工程化面试题及答案【集合】

前端工程化面试题及答案【集合】

前言&#xff1a; 欢迎浏览和关注本专栏《 前端就业宝典 》&#xff0c; 不管是扭螺丝还是造火箭&#xff0c; 多学点知识总没错。 这个专栏是扭螺丝之上要造火箭级别的知识&#xff0c;会给前端工作学习的小伙伴带来意想不到的帮助。 本专栏将前端知识拆整为零&#xff0c;主要…
阅读更多...
工业相机常见的工作模式、触发方式

工业相机常见的工作模式、触发方式

参考&#xff1a;机器视觉——工业相机的触发应用(1) - 知乎 工业相机常见的工作模式一般分为&#xff1a; 触发模式连续模式同步模式授时同步模式 触发模式&#xff1a;相机收到外部的触发命令后&#xff0c;开始按照约定时长进行曝光&#xff0c;曝光结束后输出一帧图像。…
阅读更多...
子集生成算法：给定一个集合，枚举所有可能的子集

子集生成算法：给定一个集合，枚举所有可能的子集

给定一个集合&#xff0c;枚举所有可能的子集。 &#xff08;为简单起见&#xff0c;本文讨论的集合中没有重复元素&#xff09; 1、方法一&#xff1a;增量构造法 第一种思路是一次选出一个元素放到集合中&#xff0c;程序如下&#xff1a; void print_subset(int n, int …
阅读更多...
C++系列之list的模拟实现

C++系列之list的模拟实现

&#x1f497; &#x1f497; 博客:小怡同学 &#x1f497; &#x1f497; 个人简介:编程小萌新 &#x1f497; &#x1f497; 如果博客对大家有用的话&#xff0c;请点赞关注再收藏 &#x1f31e; list的节点类 template struct list_Node { public: list_Node* _prev; list_…
阅读更多...
Tomcat服务部署和优化

Tomcat服务部署和优化

目录 一、Tomcat&#xff1a; 1、Tomcat作用&#xff1a; 2、Tomcat的核心组件&#xff1a; 3、servlet作用&#xff1a; 4、Tomcat的核心功能&#xff1a; 二、tomcat配置 一、Tomcat&#xff1a; 是一个开源的web应用服务器&#xff0c;nginx主要处理静态页面&#xff…
阅读更多...
不再受害：如何预防和应对.mallab勒索病毒攻击

不再受害：如何预防和应对.mallab勒索病毒攻击

导言&#xff1a; 我们的数据成了我们的珍宝&#xff0c;但也成了黑客们追逐的目标。其中&#xff0c;.mallab勒索病毒就是一个充满阴谋和神秘的数字威胁&#xff0c;它采用高度复杂的方法将您的数据锁在数字牢笼中。本文91数据恢复将深入探讨.mallab勒索病毒的起源、工作方式…
阅读更多...
【RabbitMQ 实战】12 镜像队列

【RabbitMQ 实战】12 镜像队列

一、镜像队列的概念 RabbitMQ的镜像队列是将消息副本存储在一组节点上&#xff0c;以提高可用性和可靠性。镜像队列将队列中的消息复制到一个或多个其他节点上&#xff0c;并使这些节点上的队列保持同步。当一个节点失败时&#xff0c;其他节点上的队列不受影响&#xff0c;因…
阅读更多...
视频转换器WinX HD Video Converter mac中文特点介绍

视频转换器WinX HD Video Converter mac中文特点介绍

WinX HD Video Converter mac是一款功能强大的视频转换器&#xff0c;它可以将各种不同格式的视频文件转换为其他视频格式&#xff0c;以便用户在各种设备上进行播放。WinX HD Video Converter是一个功能强大、易于使用的视频转换器&#xff0c;适用于各种类型的用户&#xff0…
阅读更多...
可图性判断（图论）

可图性判断（图论）

如图所示&#xff1a; 1.去arr[i]首元素&#xff0c; 后面arr[i]个元素减一 2.排序&#xff0c;以此类推 3.最后如果出现负数则不可图 4.最后元素为0&#xff0c;则可图 问题 L: Degree Sequence of Graph G代码如下&#xff1a;
阅读更多...
C#版字节跳动SDK - SKIT.FlurlHttpClient.ByteDance

C#版字节跳动SDK - SKIT.FlurlHttpClient.ByteDance

前言 在我们日常开发工作中对接第三方开放平台&#xff0c;找一款封装完善且全面的SDK能够大大的简化我们的开发难度和提高工作效率。今天给大家推荐一款C#开源、功能完善的字节跳动SDK&#xff1a;SKIT.FlurlHttpClient.ByteDance。 项目官方介绍 可能是全网唯一的 C# 版字节…
阅读更多...
基于nodejs+vue全国公考岗位及报考人数分析

基于nodejs+vue全国公考岗位及报考人数分析

目 录 摘 要 I ABSTRACT II 目 录 II 第1章 绪论 1 1.1背景及意义 1 1.2 国内外研究概况 1 1.3 研究的内容 1 第2章 相关技术 3 2.1 nodejs简介 4 2.2 express框架介绍 6 2.4 MySQL数据库 4 第3章 系统分析 5 3.1 需求分析 5 3.2 系统可行性分析 5 3.2.1技术可行性&#xff1a;…
阅读更多...
iOS的应用生命周期

iOS的应用生命周期

在iOS的原生开发中&#xff0c;我们需要特别关注两个东西&#xff1a;AppDelegate和ViewController。我们主要的编码工作就是在AppDelegate和ViewControlle这两个类中进行的。它们的类图如下图所示&#xff1a; AppDelegate是应用程序委托对象&#xff0c;它继承了UIResponder类…
阅读更多...
抖音上怎么挂小程序？制作小程序挂载抖音视频

抖音上怎么挂小程序？制作小程序挂载抖音视频

公司企业商家现在已经把抖音作为营销的渠道之一&#xff0c;目前抖音支持短视频挂载小程序&#xff0c;可方便做营销。以下给大家分享这一操作流程。 一、申请自主挂载能力 首先需要在抖音开放平台官网注册一个抖音小程序账号&#xff0c;然后申请短视频自主挂载能力。 二、搭…
阅读更多...
Kubernetes技术与架构-存储 2

Kubernetes技术与架构-存储 2

在Kubernetes集群中&#xff0c;一块持久化存储空间是可以被回收再利用&#xff0c;简称PV&#xff0c;即PersistentVolume&#xff0c;Pod实例需要使用PV的时候&#xff0c;可以使用PVC定义申请PV存储资源&#xff0c;PVC是PersistentVolumeClaim的简称&#xff0c;PV的申请分…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023