保姆级认识AVL树【C++】（精讲：AVL Insert）

news2024/7/6 19:36:06

目录

前言

一，概念

二，定义

三，insert

1. 插入情况

情况一：

情况二：

情况三：

2. 旋转方法

法一：左单旋法

法二：右单旋法

法三：先左后右双旋法

法四：先右后左双旋法

测试（判断一棵树是否是AVL树）

代码如下：

3. 随机值案例

四，删除

前言

map,set这两个容器有个共同点是： 其底层都是按照二叉搜索树来实现的，但是二叉搜索树有其自身的缺陷，假如往树中插入的元素有序或者接近有序，二叉搜索树就会退化成单支树，时间复杂度会退化成O(N)，因此map、set等关联式容器的底层结构是对二叉树进行了平衡处理，即采用平衡树来实现。

搜索二叉树请查看本篇博文：【C++】搜索二叉树底层实现_花果山~程序猿的博客-CSDN博客

一，概念

二叉搜索树虽可以缩短查找的效率，但 如果数据有序或接近有序二叉搜索树将退化为单支树，查找元素相当于在顺序表中搜索元素，效率低下。因此，两位俄罗斯的数学家G.M.Adelson-Velskii 和E.M.Landis在1962年发明了一种解决上述问题的方法： 当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度。
一棵AVL树或者是空树，或者是具有以下性质的二叉搜索树：
1. 它的左右子树都是AVL树
2. 左右子树高度之差(简称平衡因子)的绝对值不超过 1  (-1/0/1) （AVL树不一定用平衡因子进行实现）
如果一棵二叉搜索树是高度平衡的，它就是AVL树。如果它有n个结点，其高度可保持在 O(log_2 n)，搜索时间复杂度O(log_2 n)。

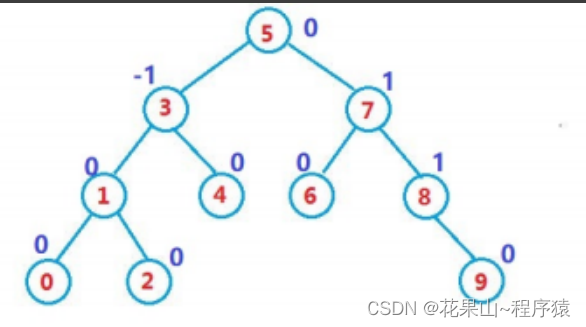
二，定义

为方便循序渐进的学习，这里只放最出初始的树结点定义。

template <class K, class V>
class AVL_Data
{
public:
	pair<K, V> _kv;
	AVL_Data<K, V>* left = nullptr;
	AVL_Data<K, V>* right = nullptr;
	AVL_Data<K, V>* parent = nullptr;
	int _bf = 0; // ballance factor

	AVL_Data(const pair<K, V>& p)
		:_kv(p)
	{}

};

上面定义在后面会进行完善修改。

三，insert

根据前面搜索二叉树的经验我们能快速写完插入函数，但AVL树是特殊的搜索二叉树，我们需要对树的高度进行调整。那么我们插入时就会遇到三种情况：

1. 插入情况

情况一：

情况二：

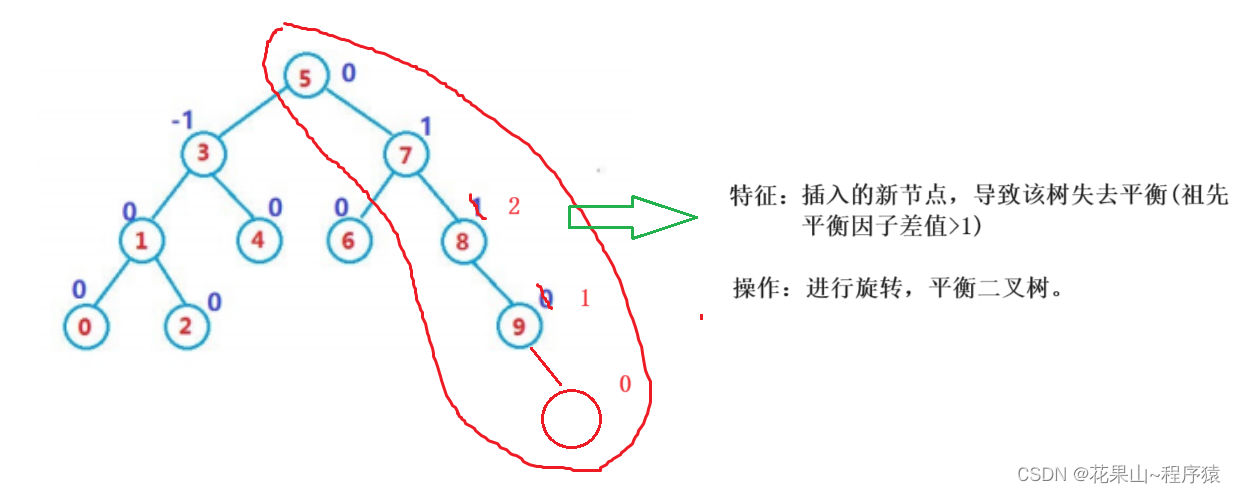
情况三：

代码实现如下：

template <class K, class V>
class AVL_Tree
{
	typedef AVL_Data<K, V>  AVL_Data;

	AVL_Data* root = nullptr;

public:
	bool insert(const pair<K, V>& p)
	{
		AVL_Data* new_a_d = new AVL_Data(p);
		if (!root)
		{
			root = new_a_d;
		}
		else
		{
			AVL_Data* cur = root;
			AVL_Data* parent = nullptr;
			while (cur)
			{
				if (p.first < cur->_kv.first)
				{
					parent = cur;
					cur = cur->left;
				}
				else if (p.first > cur->_kv.first)
				{
					parent = cur;
					cur = cur->right;
				}
				else
				{
					delete(new_a_d); // 插入失败，删除新建结点
					return false;
				}
			}

			if (p.first < parent->_kv.first)
			{
				parent->left = new_a_d;
			}
			else
			{
				parent->right = new_a_d;
			}
			new_a_d->parent = parent;

			cur = new_a_d;
			//完成插入，进行平衡
			while (parent)
			{   // 插入，修改parent平衡因子
				if (cur == parent->right)
				{
					parent->_bf++;
				}
				else
				{
					parent->_bf--;
				}

				// 判断parent平衡因子是否是0，如果非0则需要向祖先更新平衡因子
				if (parent->_bf == 1 || parent->_bf == -1)
				{
					cur = parent;
					parent = parent->parent;
				}
				else if (parent->_bf == 0)
				{
					break;
				}
				else if(parent->_bf == 2 || parent->_bf == -2)
				{ 
					// 处理绝对值大于1,下面代码目的是记录未修改的平衡因子。
					// 需要旋转处理，这个我们下面再讲
					cur = parent;
					parent = parent->parent;
				}
				else
				{
					// 出现其他情况，在插入时这棵AVL树本身就是异常AVL树
					assert(false);
				}
			}
			return true;
		}
		
	}
};

2. 旋转方法

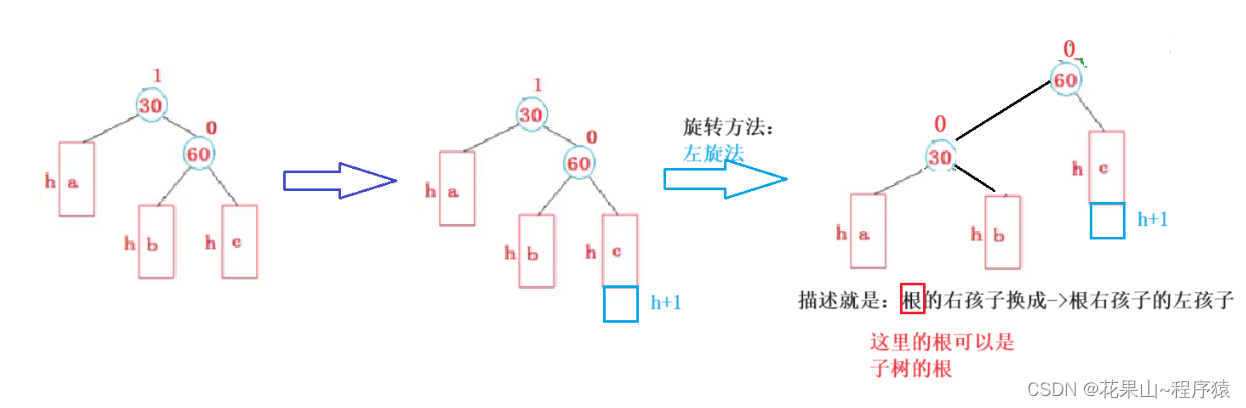
法一：左单旋法

我们以下面图为讲解例子，a,b,c表示的是子树。

h 表示子树的高度。

 请看下面场景:

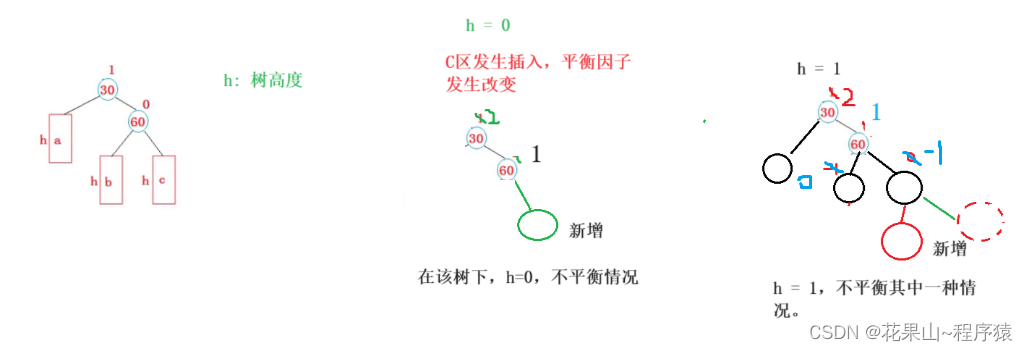
h = 3, 4...组合方式会更多，这里画出图没什么意义，问题是失去平衡我们如何解决？？ 

通过下面方法解决：

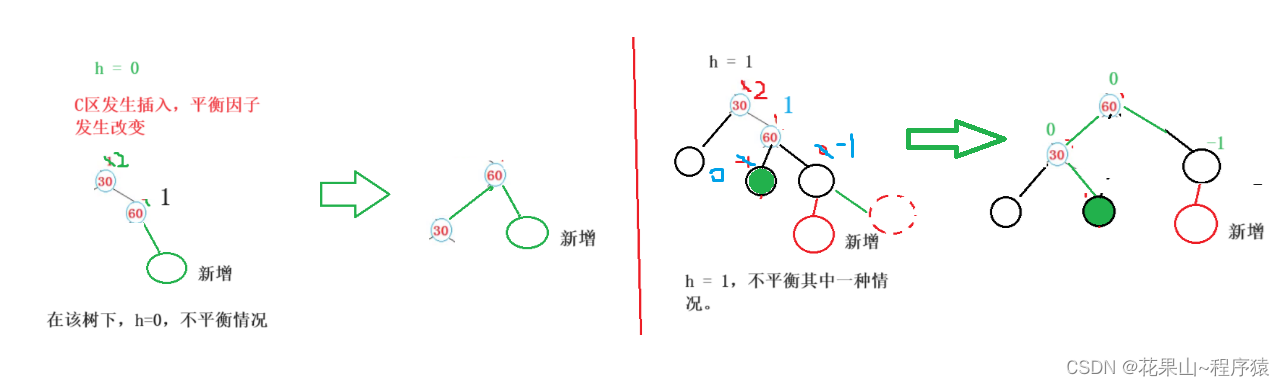
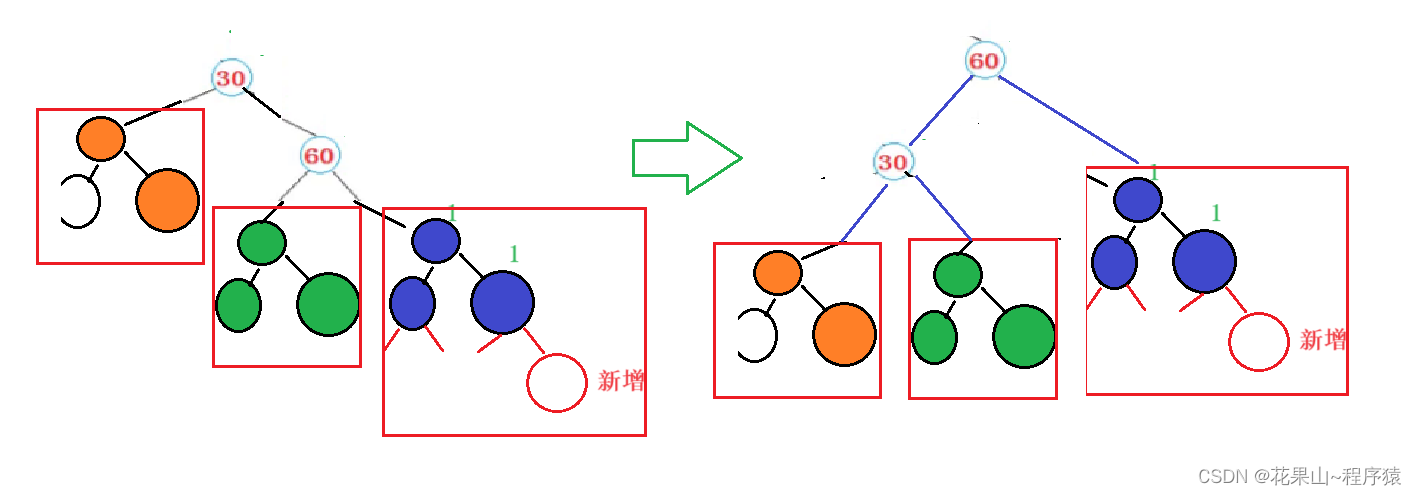
总结：

1. 右边高，则向左旋转。

2. C树发生插入，平衡因子发生改变，进而发生旋转。

void RotateL(AVL_Data* parent)
	{
		assert(parent->right);
		AVL_Data* par = parent;
		AVL_Data* par_R = par->right;
		AVL_Data* par_RL = par->right->left;
		AVL_Data* ppnode = par->parent;

		par->right = par_RL;
		if (par_RL)
		par_RL->parent = par;

		par_R->left = par;
		par->parent = par_R;
		par_R->parent = ppnode;

		if (!ppnode)
		{
			root = par_R;
		}
		else if (ppnode->left == par)
		{
			ppnode->left = par_R;
		}
		else
		{
			ppnode->right = par_R;
		}
		
		par->_bf = 0;
		par_R->_bf = 0;
	}

// 实验例子
    AVL_Tree<int, string> tree;
	tree.insert(make_pair(30 , "李四"));
	tree.insert(make_pair(20, "二麻子"));
	tree.insert(make_pair(60, "张三"));
	tree.insert(make_pair(45, "王五"));
	tree.insert(make_pair(75, "王五"));
	tree.insert(make_pair(65, "王五"));

法二：右单旋法

思路跟左旋法差不多，图像是相反，这里就只给场景解法模板：

h = 0, 1, 2的发生场景：

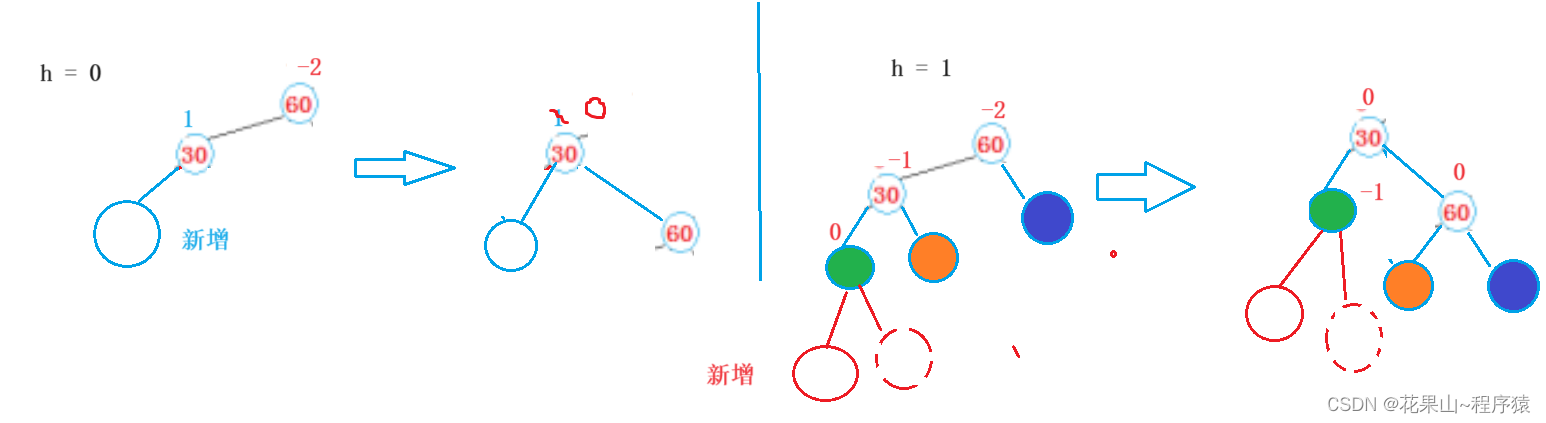
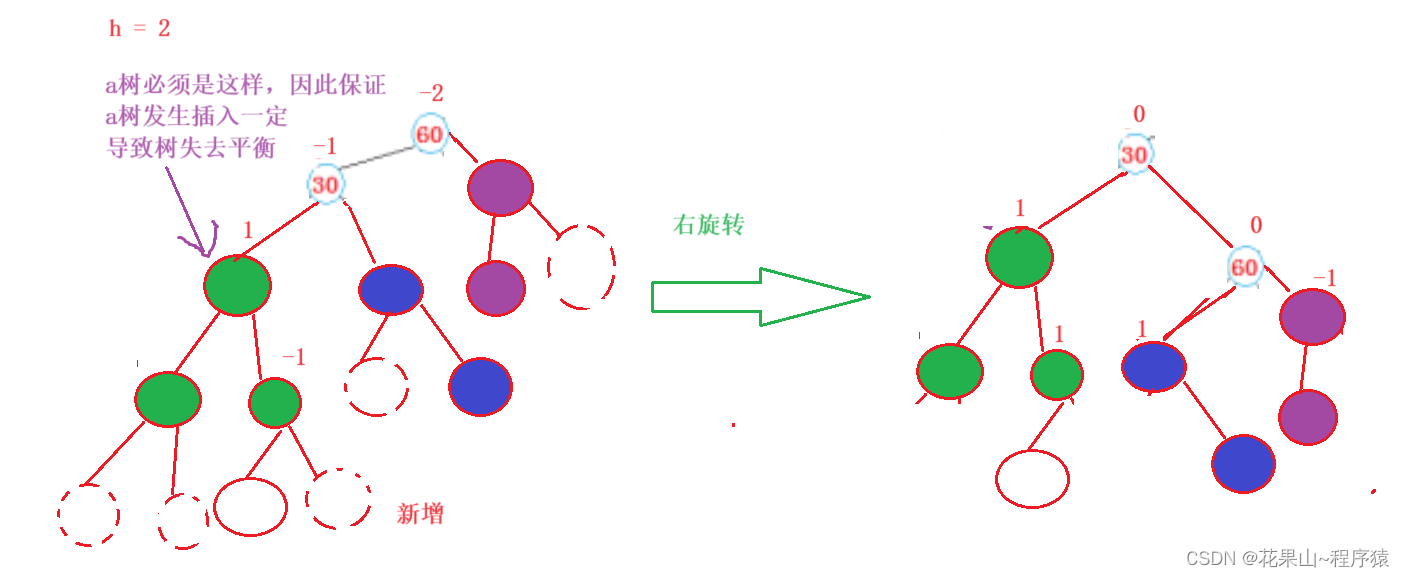
学会了法一自然会了法二：

void RotateR(AVL_Data* parent)
	{
		assert(parent->left);
		AVL_Data* par = parent;
		AVL_Data* par_L = par->left;
		AVL_Data* par_LR = par->left->right;
		AVL_Data* ppnode = par->parent;

		par->left = par_LR;
		if (par_LR)
			par_LR->parent = par;

		par_L->right = par;
		par->parent = par_L;
		par_L->parent = ppnode;

		if (!ppnode)
		{
			root = par_L;
		}
		else if (ppnode->left == par)
		{
			ppnode->left = par_L;
		}
		else
		{
			ppnode->right = par_L;
		}

		par->_bf = 0;
		par_L->_bf = 0;
	}

法三：先左后右双旋法

跟单旋一样，我们首先展示，当h = 0，1，2时需要左右双旋处理的场景。

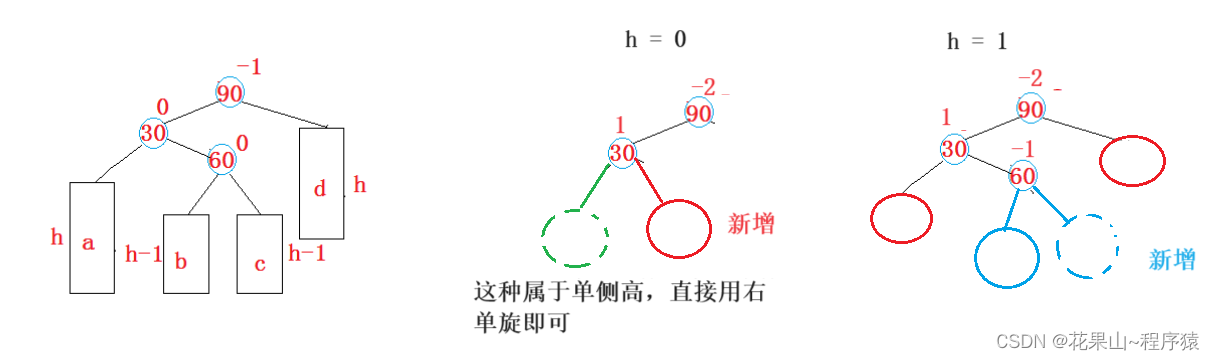
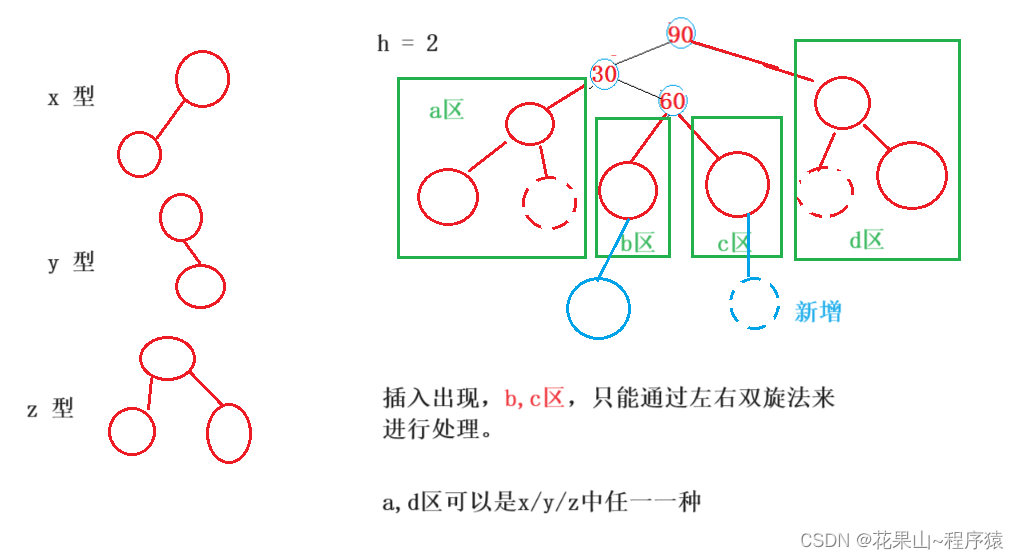
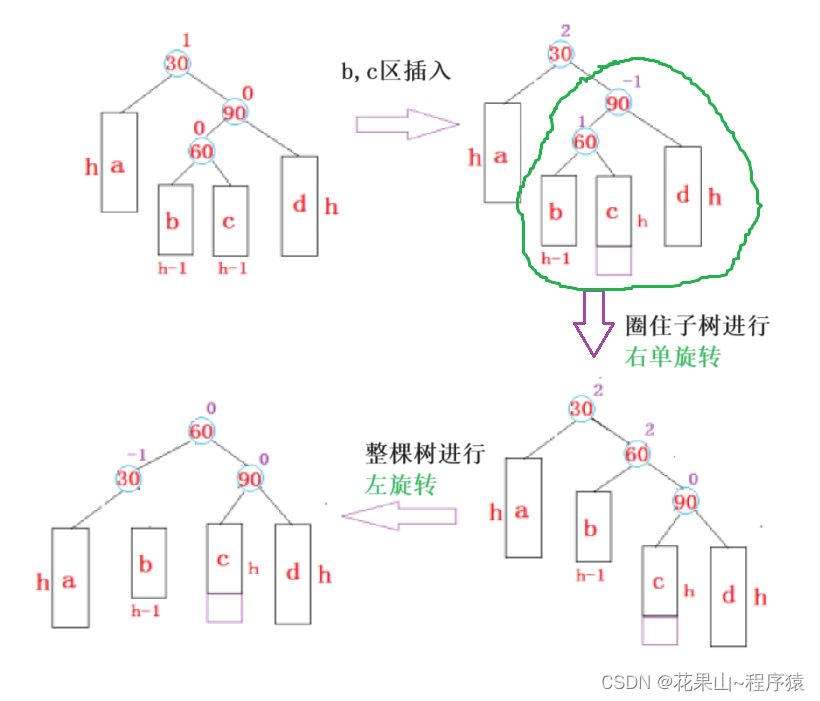
双旋法步骤变化流程，如下：

从结果来看，就是将60这个位置推上去置于“根”。

代码如下：

void RotateLR(AVL_Data* parent)
	{
		assert(parent->left);
		AVL_Data* par = parent;
		AVL_Data* par_L = par->left;
		AVL_Data* par_LR = par->left->right;
		AVL_Data* ppnode = par->parent;

		int par_LR_bf = par_LR->_bf;

		RotateL(par_L);
		RotateR(par);

		if (par_LR_bf == -1)
		{
			par->_bf = 1;
			par_L->_bf = 0;
		}
		else if (par_LR_bf == 1)
		{
			par->_bf = 0;
			par_L->_bf = -1;
		}
		else if (par_LR_bf == 0)
		{
			par->_bf = 0;
			par_L->_bf = 0;
		}
		else
		{
			assert(false);
		}
		par_LR->_bf = 0;
	}

// 测试案例
void Test_insert_L()
{
	AVL_Tree<int, string> tree;
	tree.insert(make_pair(90, "李四"));
	tree.insert(make_pair(30, "二麻子"));
	tree.insert(make_pair(100, "张三"));
	tree.insert(make_pair(25, "王五"));
	tree.insert(make_pair(60, "王五"));
	tree.insert(make_pair(50, "王五"));
}

法四：先右后左双旋法

我们学会法三后，照葫芦画瓢即可。

各场景： 

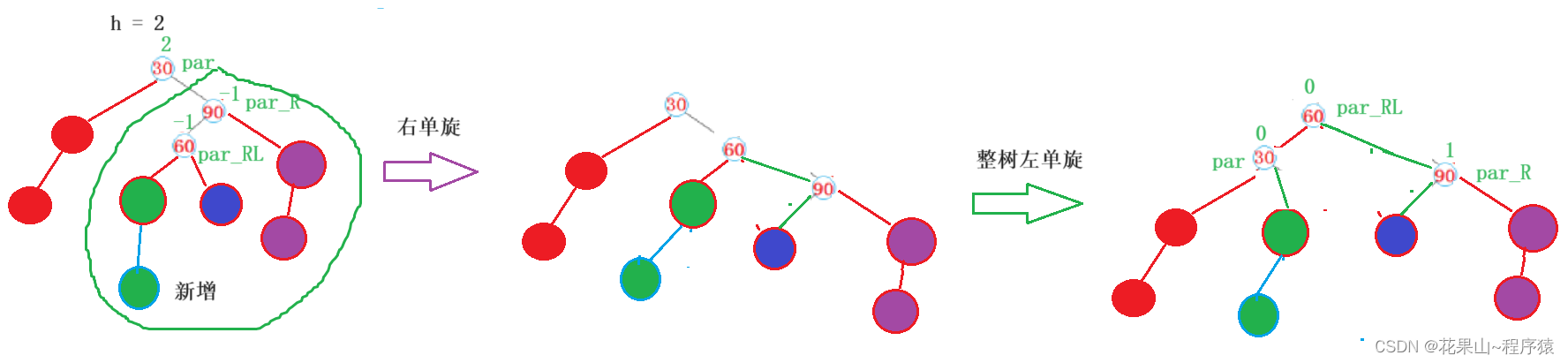
代码：

void RotateRL(AVL_Data* parent)
	{
		assert(parent->right);
		AVL_Data* par = parent;
		AVL_Data* par_R = par->right;
		AVL_Data* par_RL = par->right->left;
		AVL_Data* ppnode = par->parent;

		int par_RL_bf = par_RL->_bf;

		RotateR(par_R);
		RotateL(par);

		if (par_RL_bf == -1)
		{
			par->_bf = 0;
			par_R->_bf = 1;
		}
		else if (par_RL_bf == 1)
		{
			par->_bf = -1;
			par_R->_bf = 0;
		}
		else if (par_RL_bf == 0)
		{
			par->_bf = 0;
			par_R->_bf = 0;
		}
		else
		{
			assert(false);
		}
		par_RL->_bf = 0;
	}

// 测试案例
void Test_insert_L()
{
	AVL_Tree<int, string> tree;
	tree.insert(make_pair(30, "李四"));
	tree.insert(make_pair(20, "二麻子"));
	tree.insert(make_pair(90, "张三"));
	tree.insert(make_pair(15, "王五"));
	tree.insert(make_pair(60, "王五"));
	tree.insert(make_pair(100, "王五"));
	tree.insert(make_pair(55, "王五"));
	tree.insert(make_pair(67, "王五"));
	tree.insert(make_pair(95, "王五"));
	tree.insert(make_pair(50, "王五"));
}

测试（判断一棵树是否是AVL树）

思路：

1.  检查高度（AVL中每棵子树都是AVL树）。

2.  检查平衡因子是否正确。

代码如下：

    int Hight(const AVL_Data* root)
	{
		if (root == nullptr)
			return 0;

		int left_H = Hight(root->left);
		int left_R = Hight(root->right);
		return left_H >= left_R ? left_H + 1 : left_R + 1;
	}

    bool B_balance()
	{
		return _B_balance(root);
	}
	
	bool _B_balance(const AVL_Data* root)
	{
		if (root == nullptr)
			return true;
		int left_root = Hight(root->left);
		int right_root = Hight(root->right);


		if ((right_root - left_root) != root->_bf) // 利用Hight，进行平衡因子判断
			return false; 

		return abs(left_root - right_root) < 2 && _B_balance(root->left) && _B_balance(root->right);
	}

3. 随机值案例

用这个代码多跑几次，差不多能遍历所有环境。

void Random_Test()
{
	srand(time(0));
	const size_t N = 10000000;
	AVL_Tree<int, int> t;
	for (size_t i = 0; i < N; i++)
	{
		size_t x = rand();
		t.insert(make_pair(x, x));
	}

	cout << t.B_balance() << endl;
}

快来测试自己的代码吧

insert全代码

bool insert(const pair<K, V>& p)
	{
		AVL_Data* new_a_d = new AVL_Data(p);
		if (!root)
		{
			root = new_a_d;
		}
		else
		{
			AVL_Data* cur = root;
			AVL_Data* parent = nullptr;
			while (cur)
			{
				if (p.first < cur->_kv.first)
				{
					parent = cur;
					cur = cur->left;
				}
				else if (p.first > cur->_kv.first)
				{
					parent = cur;
					cur = cur->right;
				}
				else
				{
					delete(new_a_d); // 插入失败，删除新建结点
					return false;
				}
			}

			if (p.first < parent->_kv.first)
			{
				parent->left = new_a_d;
			}
			else
			{
				parent->right = new_a_d;
			}
			new_a_d->parent = parent;

			cur = new_a_d;
			//完成插入，进行平衡
			while (parent)
			{   // 插入，修改parent平衡因子
				if (cur == parent->right)
				{
					parent->_bf++;
				}
				else
				{
					parent->_bf--;
				}

				// 判断parent平衡因子是否是0，如果非0则需要向祖先更新平衡因子
				if (parent->_bf == 1 || parent->_bf == -1)
				{
					cur = parent;
					parent = parent->parent;	
				}
				else if (parent->_bf == 0)
				{
					break;
				}
				else if (parent->_bf == -2 || parent->_bf == 2)
				{
					if (parent->_bf == 2 && cur->_bf == 1)
					{
						RotateL(parent);
						// cout << "RotateL" << endl;
					}
					else if (parent->_bf == -2 && cur->_bf == -1)
					{
						RotateR(parent);
						// cout << "RotateR" << endl;
					}
					else if (parent->_bf == -2 && cur->_bf == 1)
					{
						RotateLR(parent);
						// cout << "RotateLR" << endl;
					}
					else if (parent->_bf == 2 && cur->_bf == -1)
					{
						RotateRL(parent);
						// cout << "RotateRL" << endl;
					}
					else
					{
						// 出现其他情况，在插入时这棵AVL树本身就是异常AVL树
						// 问题出现在旋转方法
						assert(false);
					}
					break;
				}
				else
				{
					assert(false);
				}
			}
			return true;
		}
	}

四，删除

因为AVL树也是二叉搜索树，可按照二叉搜索树的方式将节点删除，然后再更新平衡因子，只不 错与删除不同的时，删除节点后的平衡因子更新，最差情况下一直要调整到根节点的位置。 具体实现学生们可参考《算法导论》或《数据结构-用面向对象方法与C++描述》殷人昆版。

下期预告： 红黑树！！！

结语

   本小节就到这里了，感谢小伙伴的浏览，如果有什么建议，欢迎在评论区评论，如果给小伙伴带来一些收获请留下你的小赞，你的点赞和关注将会成为博主创作的动力。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1140905.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

67 内网安全-域横向smbwmi明文或hash传递

67 内网安全-域横向smbwmi明文或hash传递

#知识点1: windows2012以上版本默认关闭wdigest&#xff0c;攻击者无法从内存中获取明文密码windows2012以下版本如安装KB2871997补丁&#xff0c;同样也会导致无法获取明文密码针对以上情况&#xff0c;我们提供了4种方式解决此类问题 1.利用哈希hash传递(pth&#xff0c;ptk等…
阅读更多...
递归为什么这么难？一篇文章带你了解递归

递归为什么这么难？一篇文章带你了解递归

递归为什么这么难&#xff1f;一篇文章带你了解递归 美国计算机科学家——彼得多伊奇(L Peter Deutsch)在《程序员修炼之道》(The Pragmatic Programmer)一书中提到“To Iterate is Human, to Recurse, Divine”——我理解的这句话为&#xff1a;人理解迭代&#xff0c;神理解…
阅读更多...
电脑下载视频号视频:微信视频号如何下载到电脑桌面上？

电脑下载视频号视频:微信视频号如何下载到电脑桌面上？

很多人做视频的时候需要将视频号的视频下载到电脑上&#xff0c;该如何操作呢&#xff1f;接下来我们通过电脑下载视频号视频希望对大家有所帮助。 方法一&#xff1a;使用在线视频下载网站 有一些在线视频下载网站可以帮助你从视频号上下载视频到电脑。你只需将视频的链接复制…
阅读更多...
三个禁止使用U盘的方案

三个禁止使用U盘的方案

三个禁止使用U盘的方案 安企神U盘管理系统下载使用 U盘是一种小型便携式的存储设备&#xff0c;可以方便地传输和存储各种类型的数据&#xff0c;但也因此带来了一些安全隐患。在一些特殊的场合&#xff0c;如公司、商业场地等&#xff0c;为了保护内部数据被盗取外泄&#x…
阅读更多...
怎么才能写好宣传软文？媒介盒子为你揭秘

怎么才能写好宣传软文？媒介盒子为你揭秘

数字化时代改变了企业的宣传方式&#xff0c;软文成为企业宣传的主要方式&#xff0c;但是企业真的会写宣传软文吗&#xff1f;为什么宣传软文不起效果&#xff1f;下面媒介盒子先和大家分享宣传软文的写作技巧 一、为什么要宣传 企业为什么需要宣传&#xff0c;主要有三类情况…
阅读更多...
JS实现商品SKU

JS实现商品SKU

<!DOCTYPE html> <html> <head><title>商品SKU</title><link rel"stylesheet" href"element/css/element.css"><style>*{ margin:0; padding:0px; box-sizing: border-box; }ul,li{ list-style-type: none;}bod…
阅读更多...
Python武器库开发-高级特性篇(八)

Python武器库开发-高级特性篇(八)

高级特性篇(八) 高阶函数 Python作为一门高级编程语言&#xff0c;拥有着强大的函数式编程能力。其中高阶函数就是Python函数式编程的重要组成部分。在Python中&#xff0c;函数可以被当作变量一样进行操作&#xff0c;包括作为参数传递给其他函数&#xff0c;或者作为返回值…
阅读更多...
DBSCAN算法c++实现

DBSCAN算法c++实现

首先计算出距离每个点e以内的点&#xff0c;如果个数>minPts,则找出它的直接密度可达和间接可达的点&#xff0c;用visited标记点是否已经在簇中&#xff0c;循环直到最后一个点。 #include <fstream> #include <vector> #include <iostream> #include &…
阅读更多...
Leetcode.树形DP

Leetcode.树形DP

目录 543.二叉树的直径 124.二叉树中的最大路径和 2246.相邻字符不同的最长路径 543.二叉树的直径 用递归来写 考虑 树形DP 维护以当前节点为根节点的最大值&#xff0c;同时返回给父节点经过当前节点的最大链的长度&#xff0c;这有个trick 当遍历到空节点的时候返回-1 递归…
阅读更多...
mq消费并发排队及幂等机制实现

mq消费并发排队及幂等机制实现

一&#xff0c;解决什么问题及实现方案 主要为了解决并发访问排队执行及重复下发保证幂等的问题 实现技术方案 如何实现并发访问时&#xff0c;请求排队执行方法。Redssion 如何实现MQ重复下发时&#xff0c;保证幂等。redis 先插入一个分布式锁的话题&#xff0c;如下&am…
阅读更多...
LeetCode 740.删除并获得点数----＞打家劫舍

LeetCode 740.删除并获得点数----＞打家劫舍

前言&#xff1a;简单写写自己对这道题的拙见&#xff0c;如有意见或者建议可以联系笔者owo 首先&#xff0c;看看完整题目描述&#xff1a; 给你一个整数数组 nums &#xff0c;你可以对它进行一些操作。 每次操作中&#xff0c;选择任意一个 nums[i] &#xff0c;删除它并获…
阅读更多...
归并排序(java)

归并排序(java)

大家好我是苏麟 , 今天说说归并排序 . 归并排序 递归 正式学习归并排序之前&#xff0c;我们得先学习一下递归算法。 定义&#xff1a; 定义方法时&#xff0c;在方法内部调用方法本身&#xff0c;称之为递归. public void show(){System.out.println("aaaa")…
阅读更多...
SEACALL海外呼叫中心系统的优势包括

SEACALL海外呼叫中心系统的优势包括

SEACALL海外呼叫中心系统的优势包括 封卡封号问题解决 海外呼叫中心系统通过API开放平台能力&#xff0c;定制电话营销系统&#xff0c;提供多项功能如自动拨打、智能应答、真人语音交互等&#xff0c;帮助企业克服员工离职率高、客户资源流失严重等挑战。 - 高级管理者操控 …
阅读更多...
《实现领域驱动设计》

《实现领域驱动设计》

DDD入门 1.1 DDD是什么&#xff1f; DDD是一种软件开发方法 DDD将领域专家和开发人员聚集到一起&#xff0c;开发的软件能够反映出领域专家的思维模型。目标是&#xff1a;交付最具业务价值的软件。DDD关注业务战略&#xff1a;指引我们如何实现面向服务架构&#xff08;ser…
阅读更多...
开题报告怎么写？-案例+模板保姆级）

开题报告怎么写？-案例+模板保姆级）

以前导师让们带本科生开题报告&#xff0c;我深知开题报告在学术研究中的重要性。一个出色的开题报告能够展示学生的科学思维、研究能力和创新潜力。 在本篇博客中&#xff0c;我将为大家详细介绍如何撰写史上最强开题报告。 将从课题的 科学意义国内外研究概况和发展趋势应…
阅读更多...
SourceTree 使用

SourceTree 使用

如何拉取远程仓库&#xff1f;如何拉去远程分支&#xff1f;如何创建本地分支&#xff1f;如何删除本地分支&#xff1f;如何删除远端分支&#xff1f; 删除了远程分支&#xff0c;如果本地还有此分支&#xff0c;那么是可以通过推送本地分支来还原远端分支。如何合并本地分支&…
阅读更多...
2023中国计算机大会：蚂蚁集团连发两支百万级科研基金

2023中国计算机大会：蚂蚁集团连发两支百万级科研基金

10月26日&#xff0c;中国计算机学会&#xff08;CCF&#xff09;主办的第二十届中国计算机大会(CNCC2023)在沈阳举行。在“CCF-蚂蚁科研基金及产学研合作交流活动”上&#xff0c;蚂蚁集团发布了2023年度“CCF-蚂蚁科研基金”绿色计算及隐私计算两支百万级专项基金&#xff0c…
阅读更多...
动态代理IP怎么设置？动态代理IP有哪些应用场景？

动态代理IP怎么设置？动态代理IP有哪些应用场景？

动态代理IP是指代理服务器会根据实际IP地址的变化而变化&#xff0c;可以帮助用户隐藏真实的IP地址&#xff0c;同时可以在不同的网络环境下使用不同的代理IP地址。下面是动态代理IP的设置和应用场景&#xff1a; 一、动态代理IP怎么设置&#xff1f; 1. 手动设置代理IP地址 用…
阅读更多...
基于Arduino的物流分拣控制系统设计

基于Arduino的物流分拣控制系统设计

欢迎大家点赞、收藏、关注、评论啦 &#xff0c;由于篇幅有限&#xff0c;只展示了部分核心代码。 技术交流认准下方 CSDN 官方提供的联系方式 文章目录 概要 一、控制系统设计1.1系统方案1.2 系统工作原理1.3方案设计1.3.1快递检测电路方案设计1.3.2控制电路方案设计 二、硬件…
阅读更多...
【Java基础】File类与IO流

【Java基础】File类与IO流

File类与IO流 文章目录 File类与IO流1. java.io.File类的使用1.1 概述1.2 构造器1.3 作用 2. IO流原理及流的分类2.1 流的分类2.3 流的API 3. 节点流之一&#xff1a;FileReader\FileWriter3.1 Reader与Writer3.3 关于flush&#xff08;刷新&#xff09; 4. 节点流之二&#xf…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023