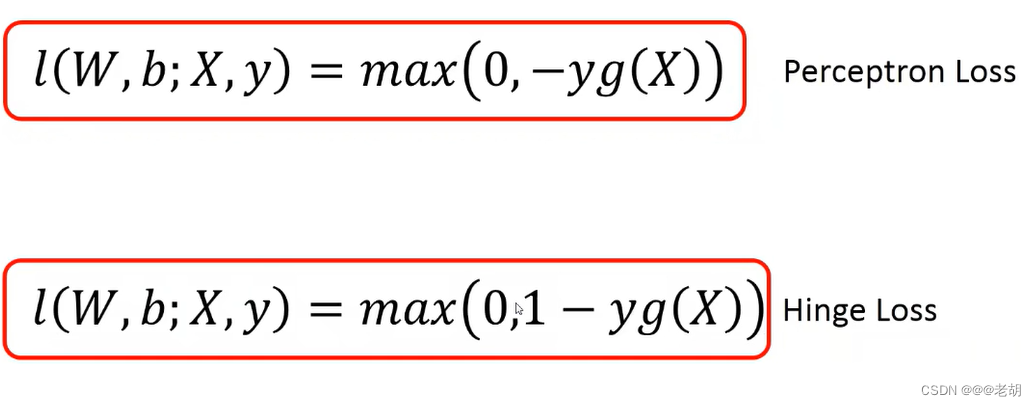文章目录
- 计算机视觉与图像处理的区别
- 人工神经元
- 感知机 - 分类任务
- Sigmoid神经元/对数几率回归
- 对数损失/交叉熵损失函数
- 梯度下降法- 极小化对数损失函数
- 线性神经元/线性回归
- 均方差损失函数-线性回归常用损失函数
- 使用梯度下降法训练线性回归模型
- 线性分类器
- 多分类器的决策面
- softmax Regression
- 训练softmax regression
- 交叉熵损失
- 解决参数冗余
- 训练softmax Classifier
- 混淆矩阵
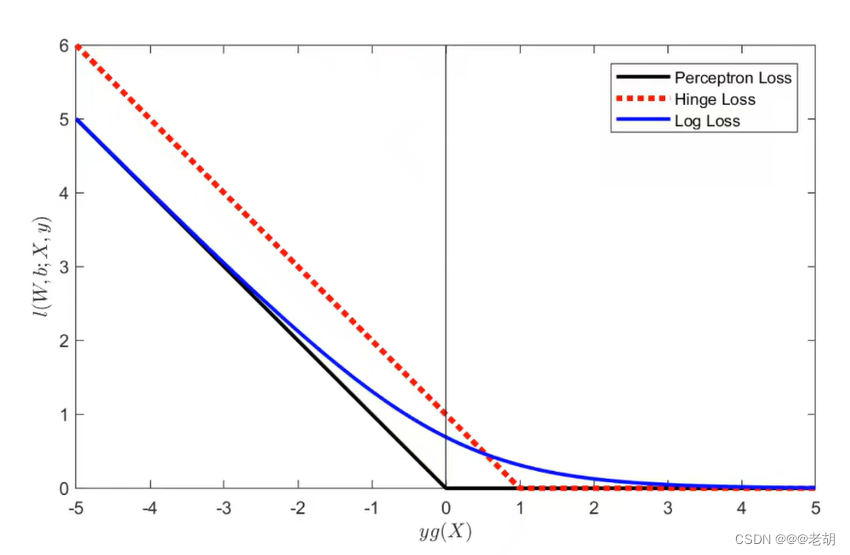
- 合页(铰链)损失
计算机视觉与图像处理的区别
-
图像处理得到的结果是处理后的图像,图像处理的目的是改善图像的质量
- 图像增强
- 图像复原
-
计算机视觉得到的结果可能是一个符号、一堆数据、一个知识
- 人脸识别
- 人脸比对
-
传统的图像识别的机器学习方法的一般流程包括:
- 特征提取→数据
- 数据→机器学习
-
为什么要提取图像的特征
- 提取有利于识别的信息,抑制与识别无关的或者对识别有干扰的信息
- 把不同尺度的图像映射到一个统一的特征空间,便于应用机器学习算法。
-
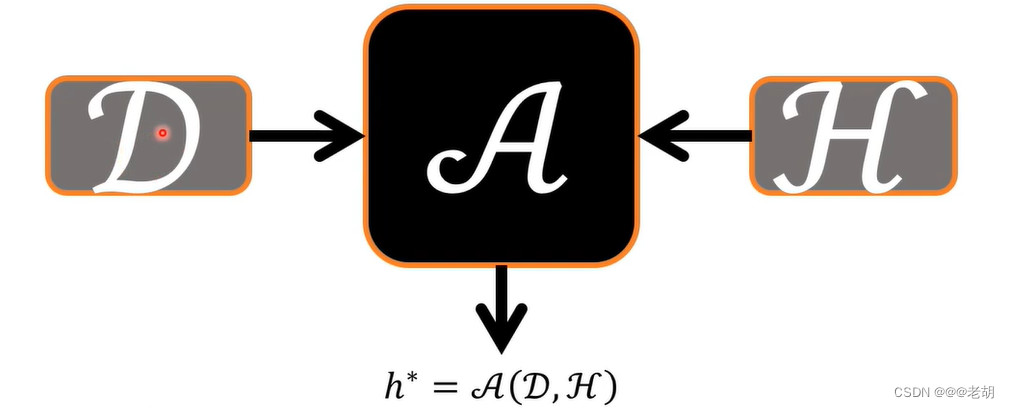
机器学习的框架:D数据,A算法,H假设空间,h* H中最好的假设(真实误差最小的假设)
-
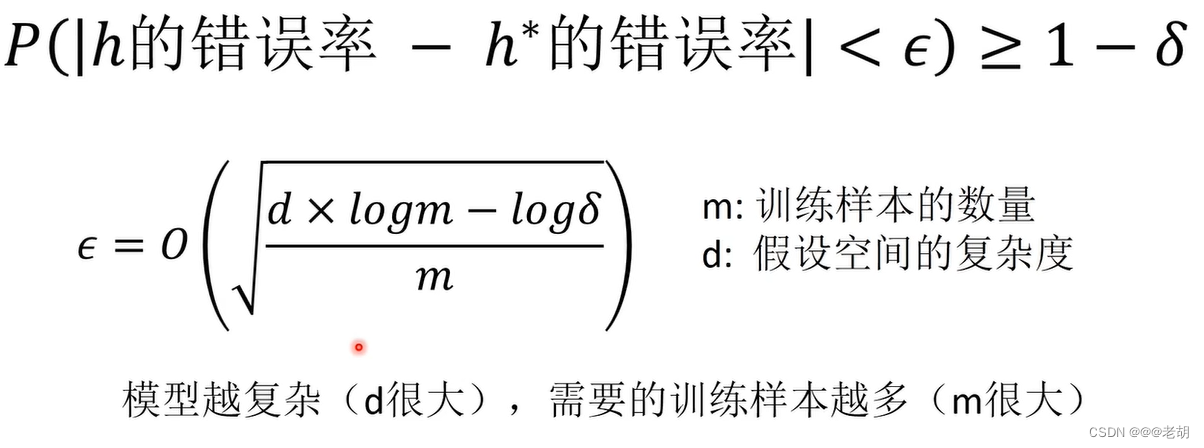
概率近似正确
人工神经元
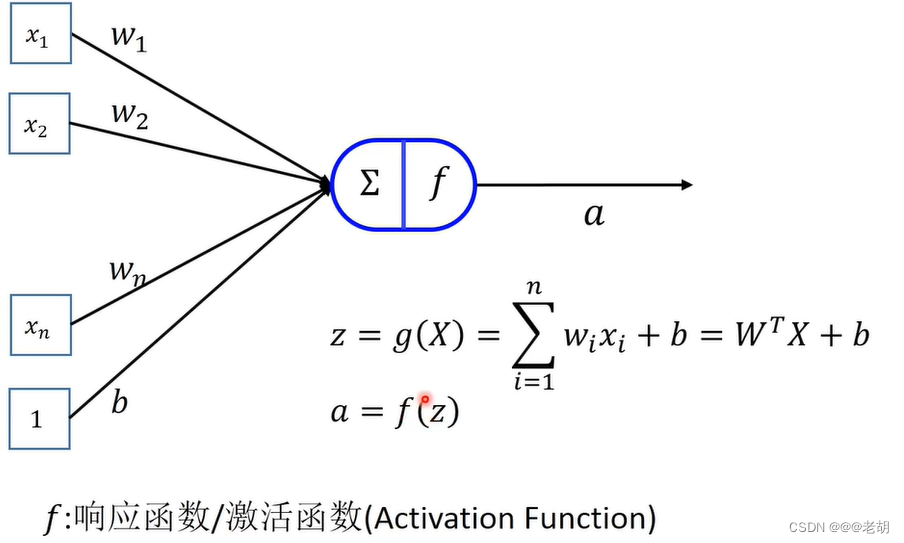
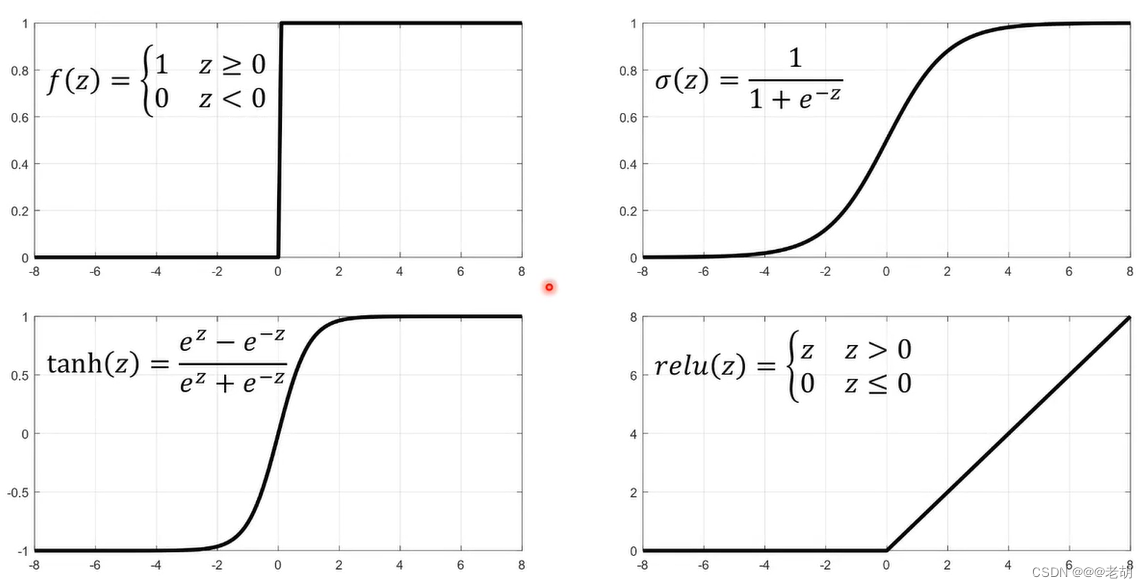
f:响应函数/激活函数一般都是非线性的函数,且一般都单调递增;常用的激活函数包括以下:
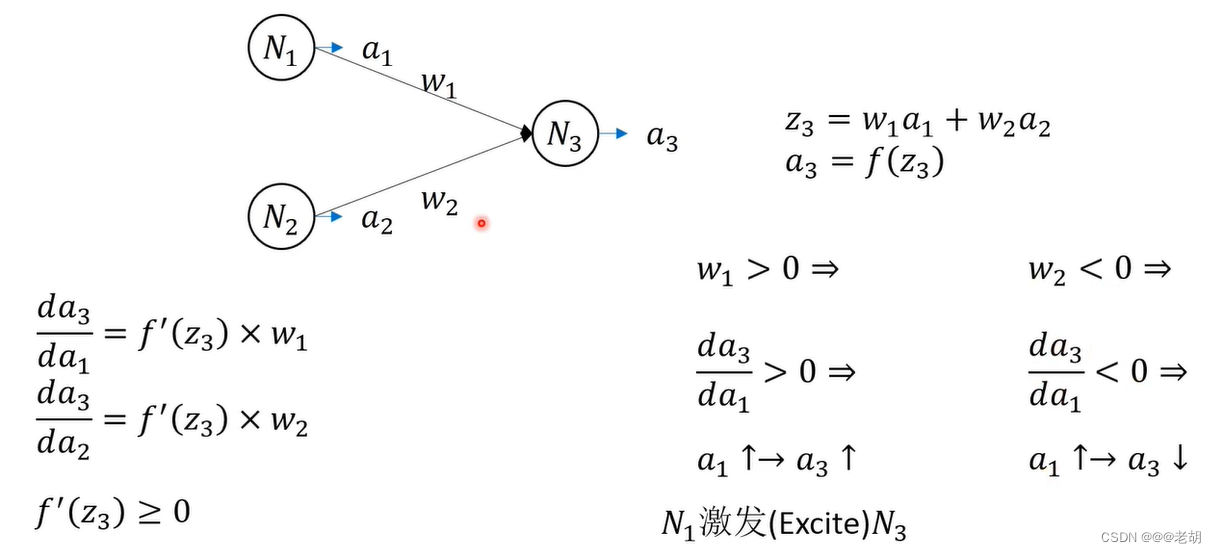
因为f是单调递增的函数,,如果 w>0,则,说明前一个神经元对后一个神经元有激活的作用;如果w<0 ,说明前一个神经元对后一个神经元有抑制作用。
感知机 - 分类任务
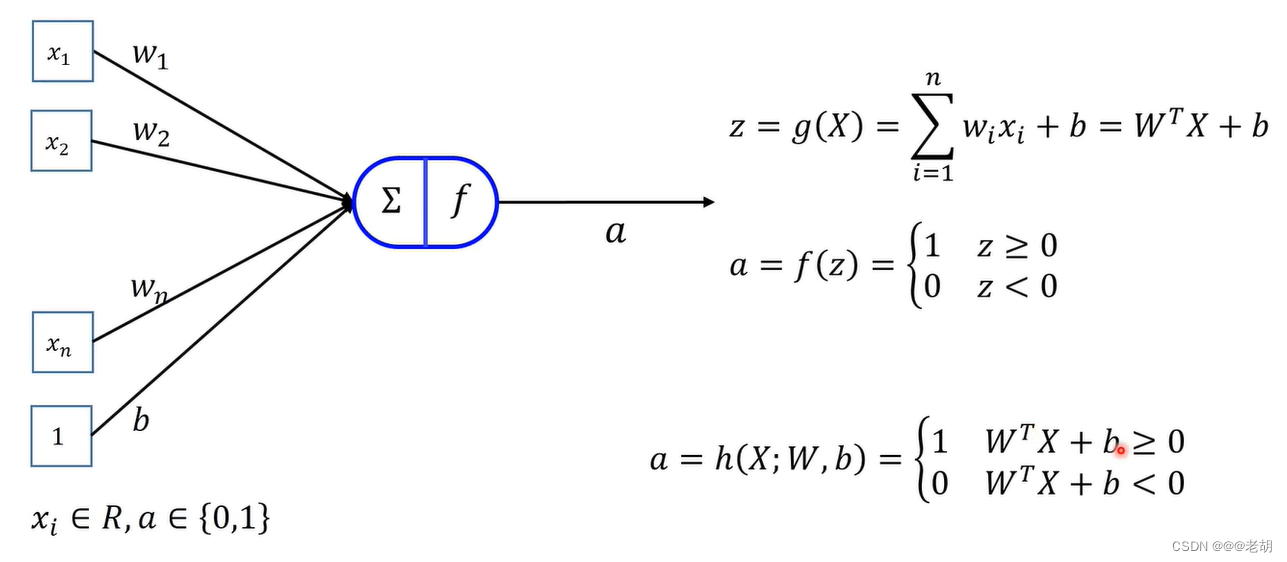
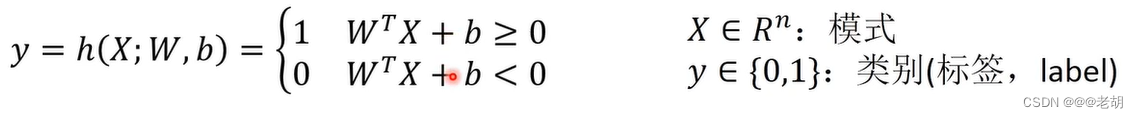
- 感知机算法在线性可分的情况下,一定可以收敛,也就是一定可以找到一个能正确分类所有样本的分类函数
- 但是同一个样本集,有可能会得到不同的解
- 不同的初始值,不同的样本处理次序产生的结果不同
- 不能得到全局最优的解
- 线性不可分的时候,算法会失败
感知机的算法

损失函数:不能处处可导

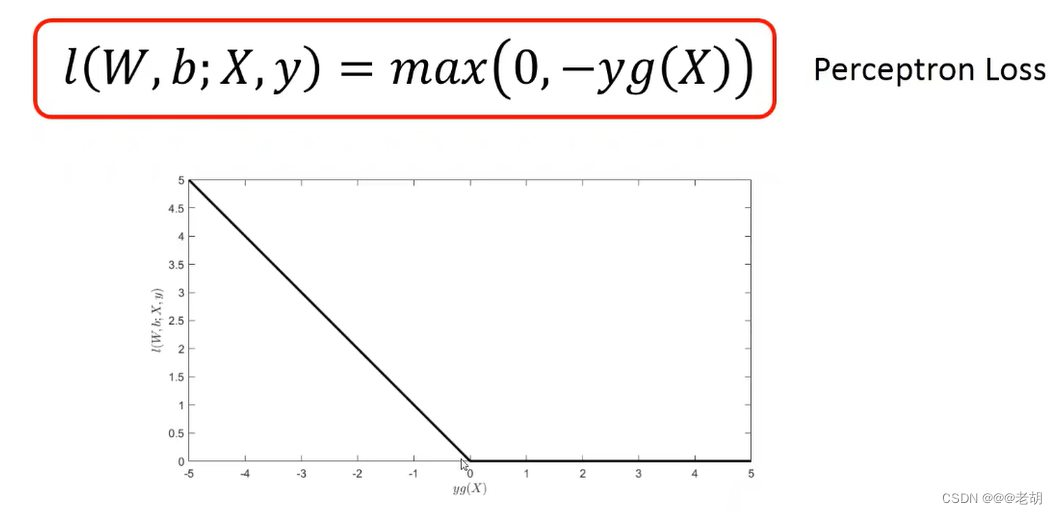
解决方法:次梯度
Sigmoid神经元/对数几率回归
只有激活函数的不同,sigmoid处处连续可导,输出的是对数几率
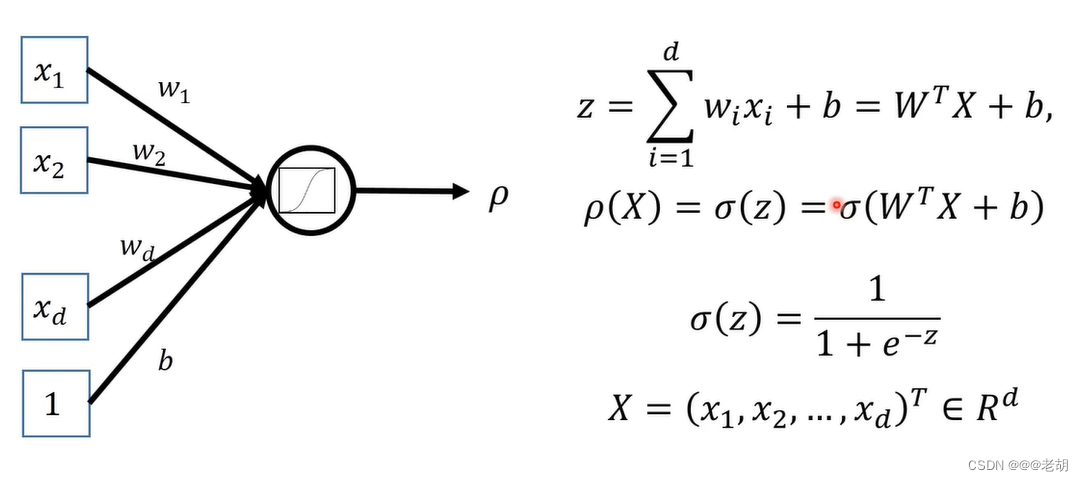
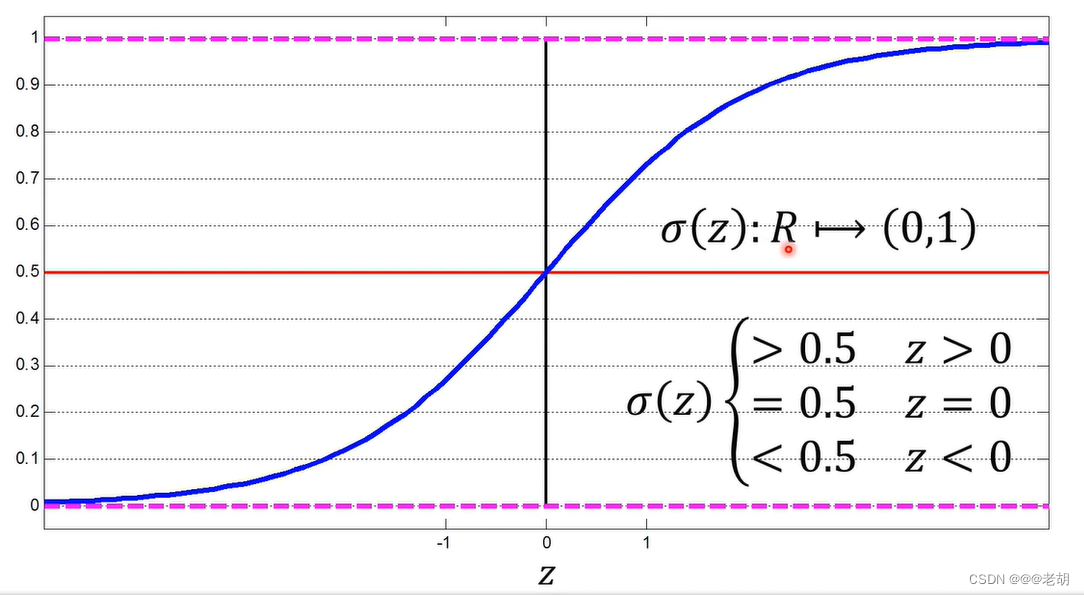
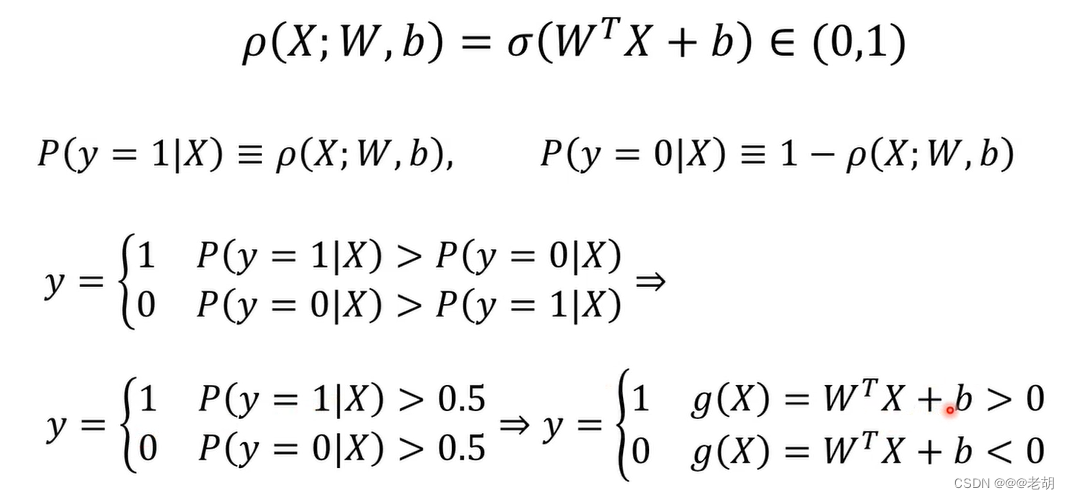
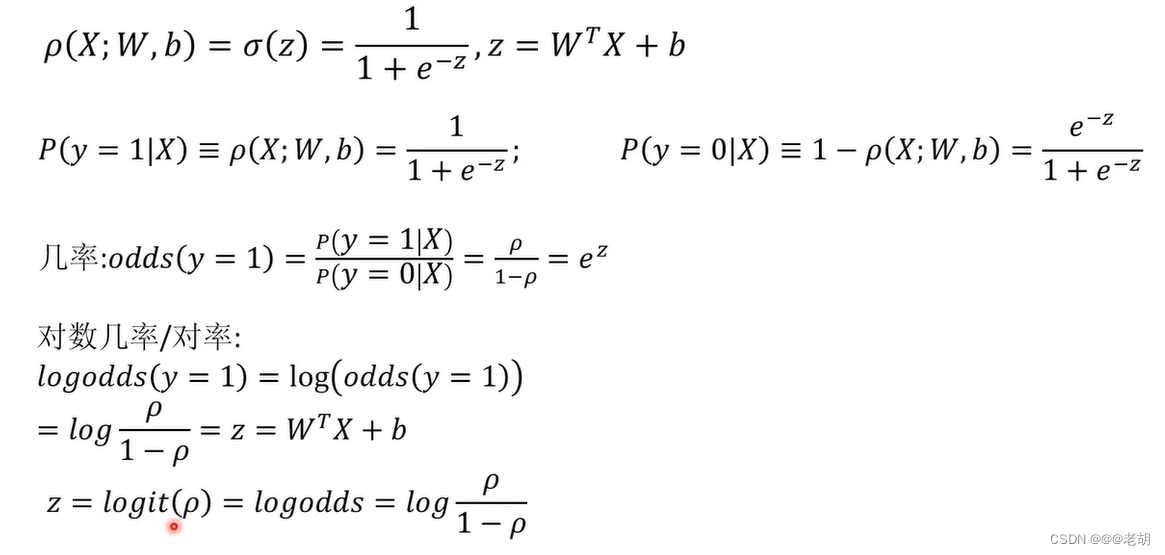
对数损失/交叉熵损失函数
损失函数通过比较模型对样本X的预测结果与样本的真实类别y之间的差异,计算损失,差异越大,损失越大,差异越小,损失越小。
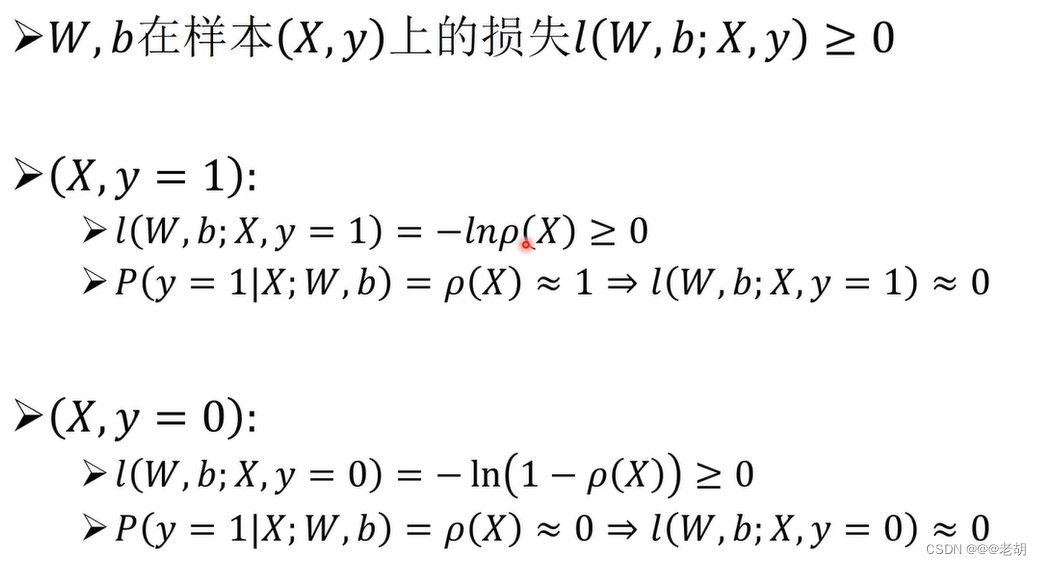
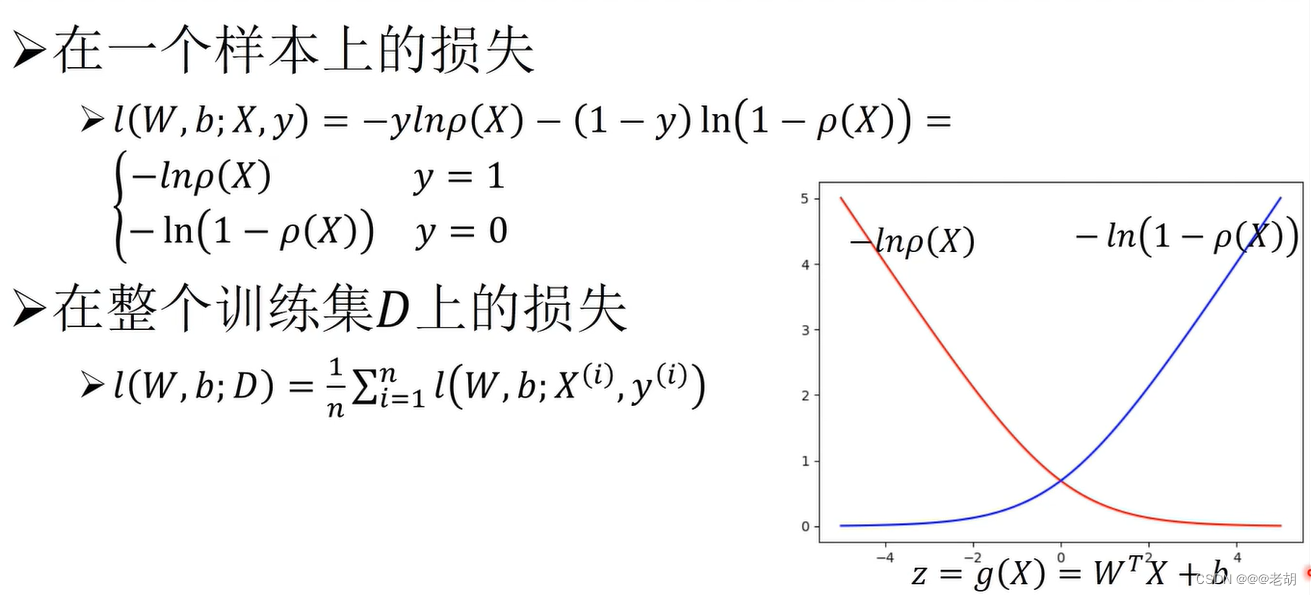
梯度下降法- 极小化对数损失函数
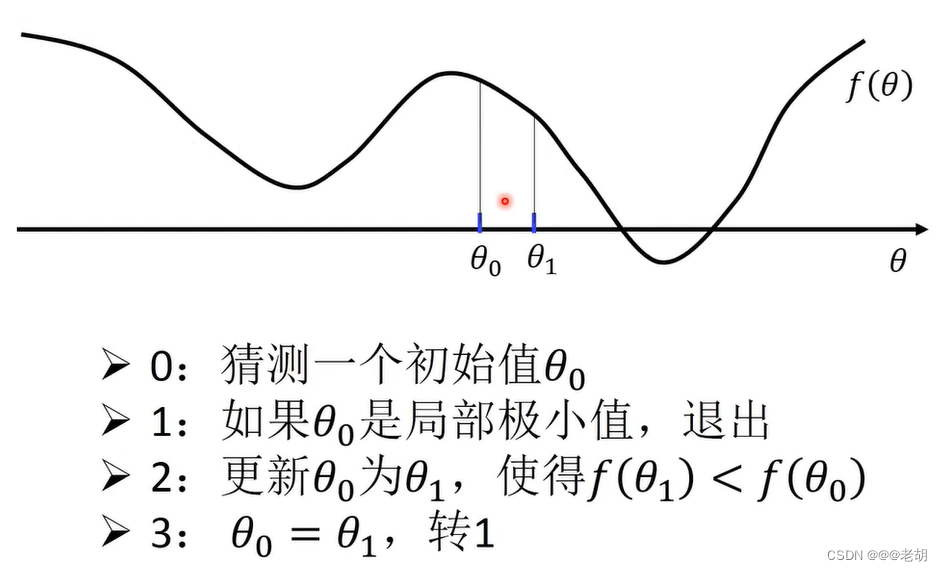
线性神经元/线性回归
神经元有两个部分组成:收集信号的过程和激活的过程,收集信号如果是使用线性过程(累加)就是线性神经元。至于收集到的信号能不能激活下一个神经元,要看激活函数的过程,这个过程一般不是线性的。
均方差损失函数-线性回归常用损失函数
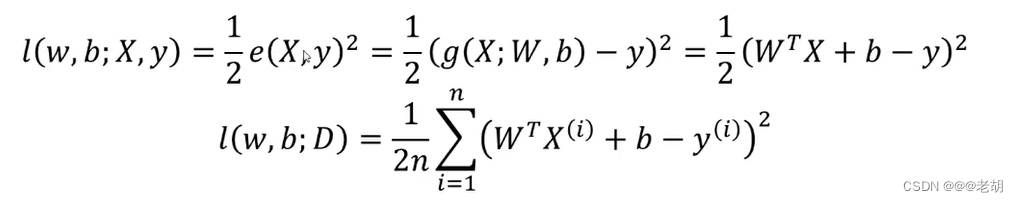
使用梯度下降法训练线性回归模型
是对w,b进行更新
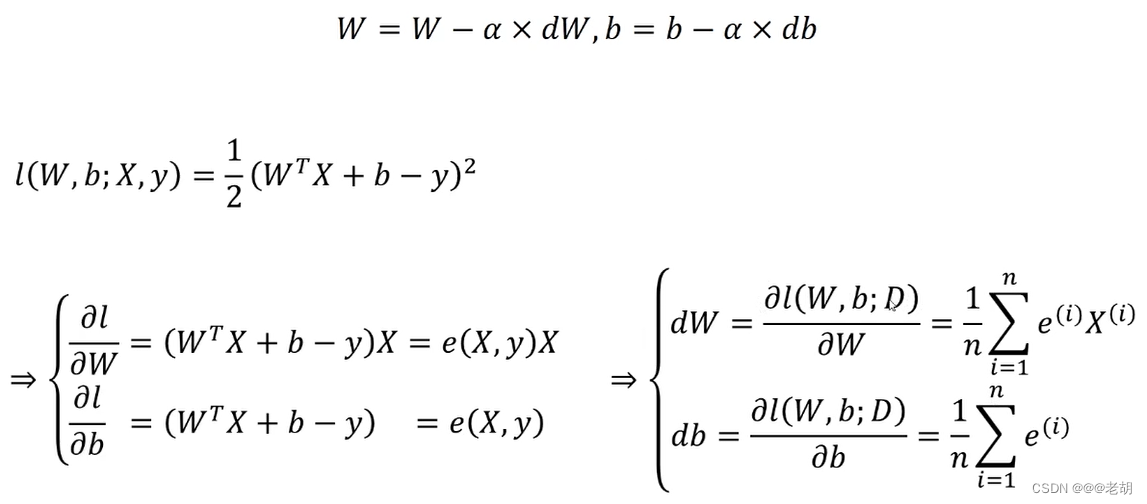
一元导数与微分的关系:
d
f
/
d
x
=
f
′
一元导数与微分的关系:df/dx=f'
一元导数与微分的关系:df/dx=f′
全微分:
d
F
=
(
α
F
/
α
x
)
d
x
+
(
α
F
/
α
y
)
d
y
全微分:dF=(αF/αx) dx+(αF/αy) dy
全微分:dF=(αF/αx)dx+(αF/αy)dy
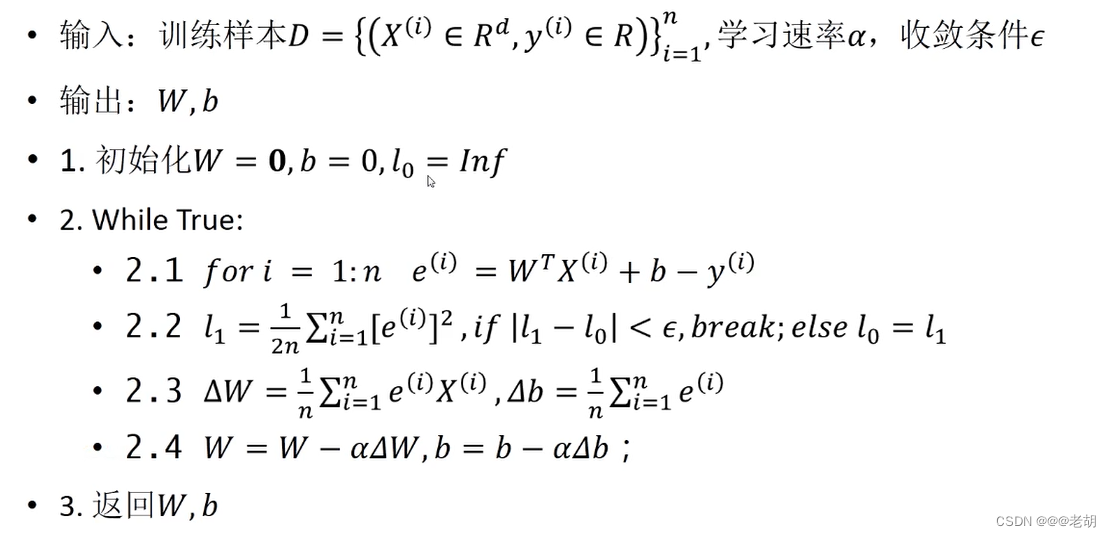
线性分类器
α
∗
β
=
∣
α
∣
∗
∣
β
∣
c
o
s
<
α
,
β
>
(
α
,
β
为向量),其中
∣
β
∣
c
o
s
<
α
,
β
>
称为
β
在
α
上的投影
α*β=|α|*|β|cos<α,β>(α,β为向量),其中|β|cos<α,β>称为β在α上的投影
α∗β=∣α∣∗∣β∣cos<α,β>(α,β为向量),其中∣β∣cos<α,β>称为β在α上的投影

多分类器的决策面
决策面是可以把各种分类分开的一个面,在三级分类中,决策面应该在超平面的角平分线处划分
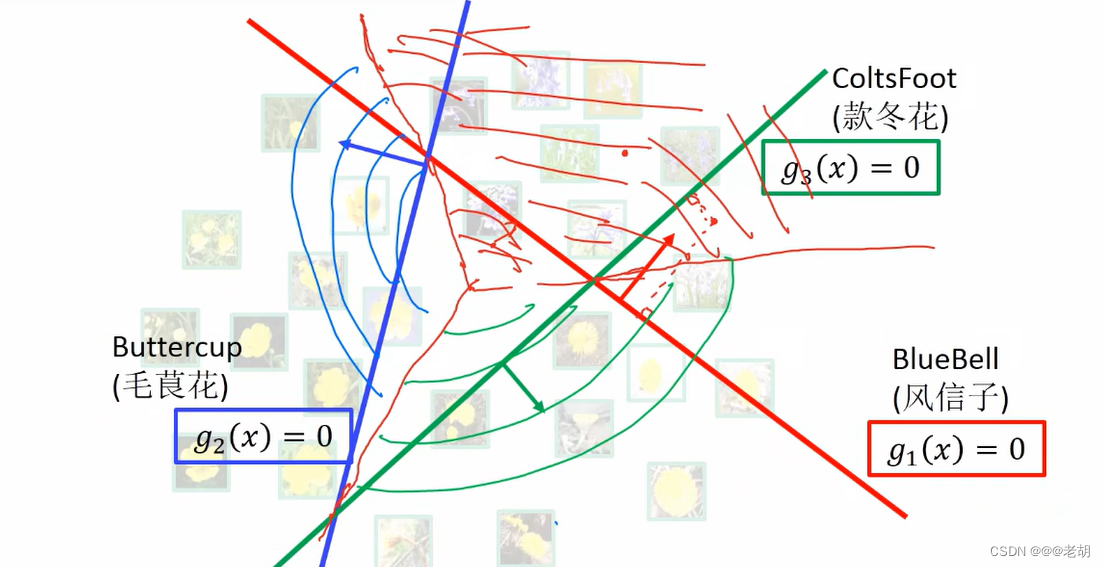
softmax Regression

- 这种argmax会把打分最高的结果设为1,其他的结果设为0;但是这种投影的坏处在于只看得到分类,看不到分类的置信为多少,所以引入了softmax Regression( e z 变成正数,正数加和为分母,求概率 e^z变成正数,正数加和为分母,求概率 ez变成正数,正数加和为分母,求概率)

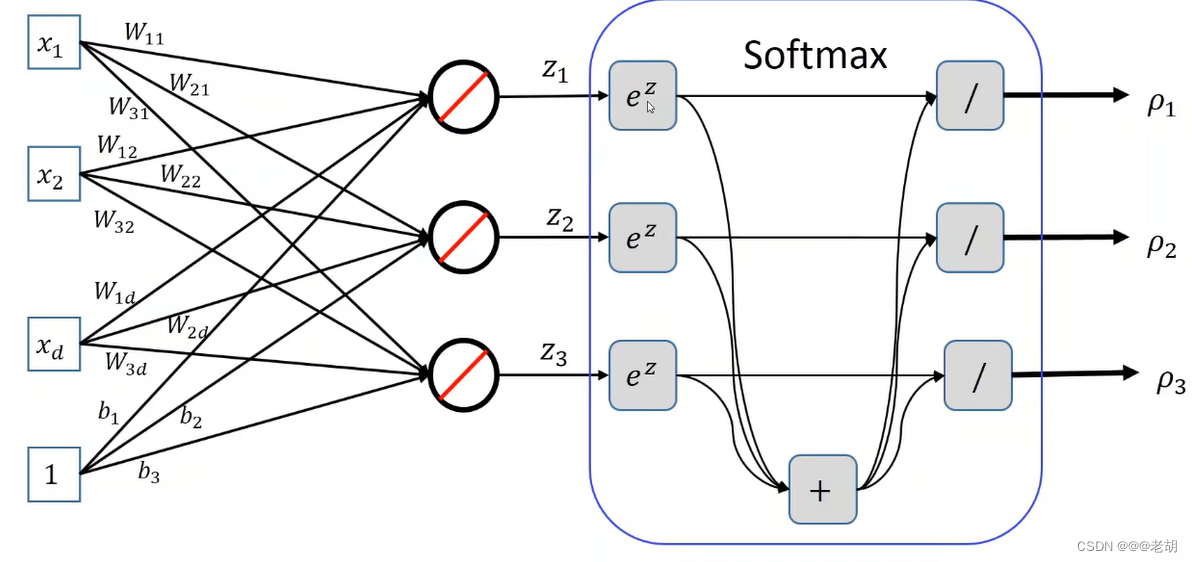
softmax的决策规则就是:寻找概率最大的作为分类的输出,又因为e函数是单调递增的,所以只要z最大,则概率就会最大。
训练softmax regression
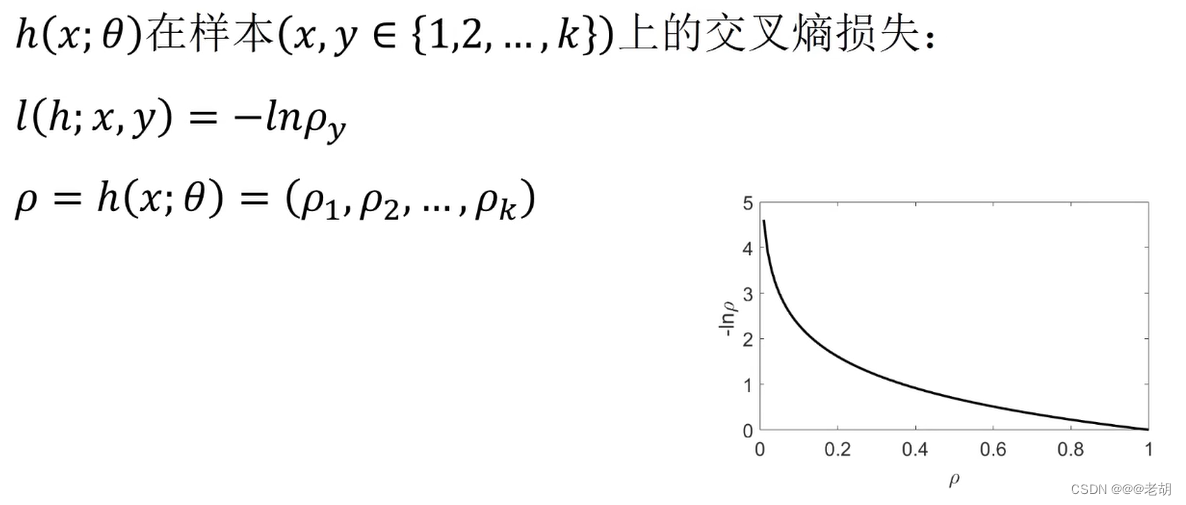
这里要特别注意,这里计算损失函数的那个概率,是真实样本所对应的概率,不是预测值的那个概率
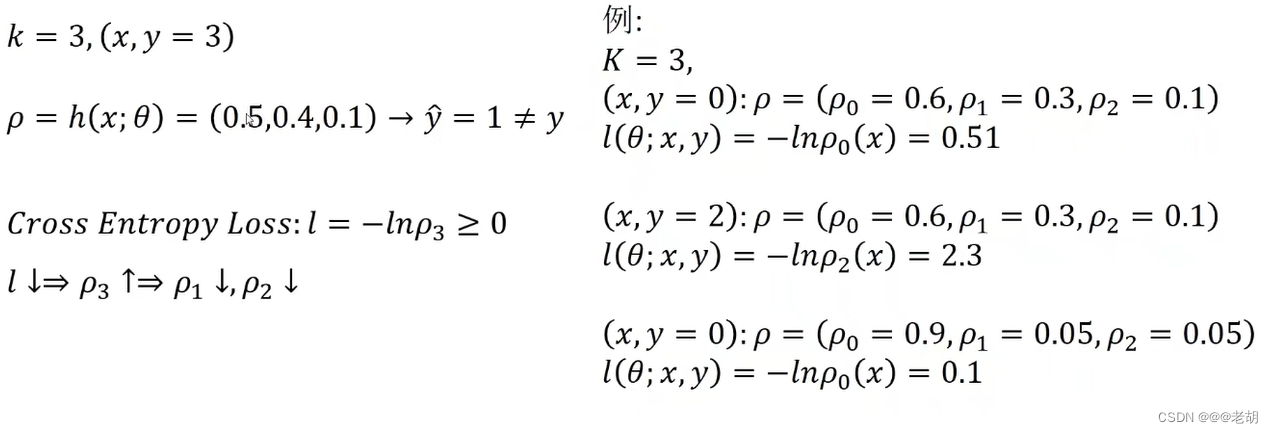
训练过程
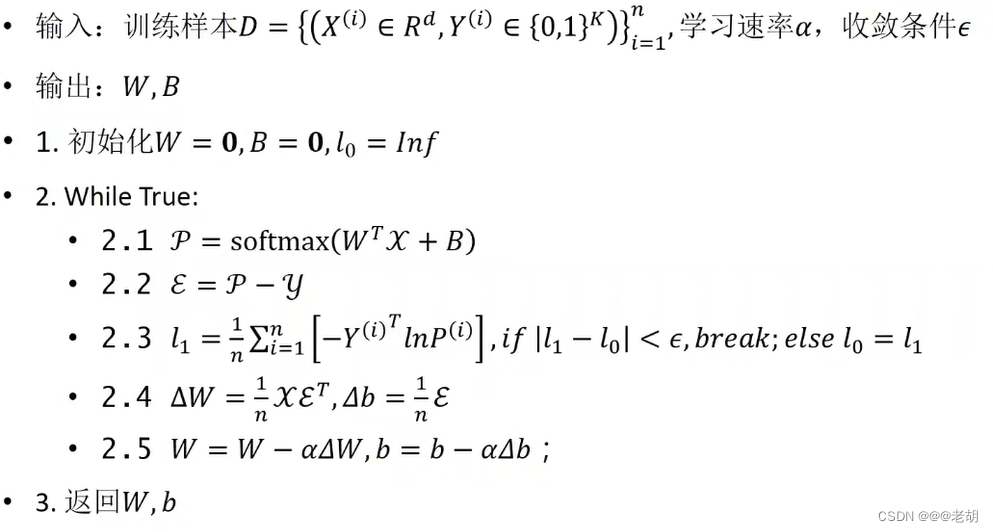
交叉熵损失


解决参数冗余
可以使用一个正则化项:选择损失函数小且Ω也小的
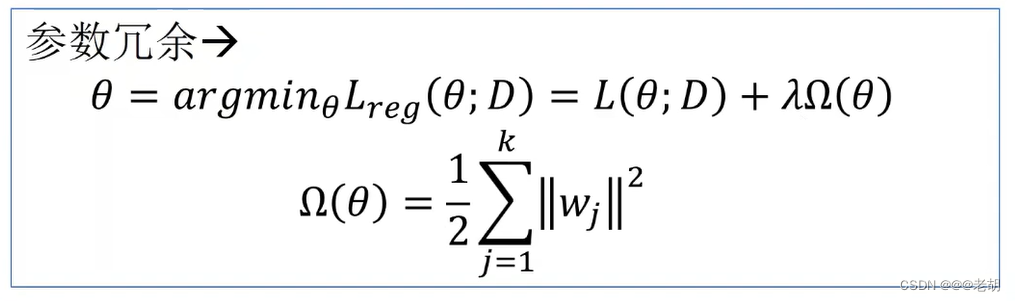
训练softmax Classifier



混淆矩阵
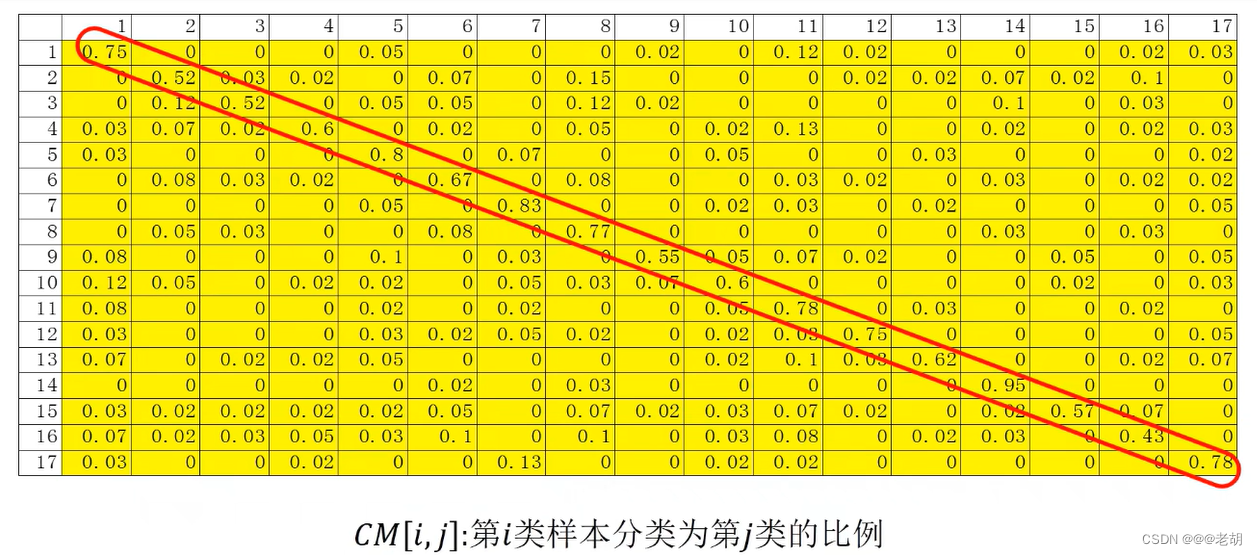
对角线上的表示第k个类别的精度,混淆矩阵可以清晰的看到哪一个类别的分类情况较好(精度高),哪一个类别的分类情况不好(精度第),以及具体的分类情况是什么
合页(铰链)损失