目录
一,什么是搜索二叉树?
二,搜索二叉树的实现
非递归实现
节点与类成员
插入
查找
删除
递归实现
插入
查找
删除
一,什么是搜索二叉树?
搜索二叉树(Binary Search Tree)是一种常见的二叉树数据结构,它的每个节点都包含一个关键字,且每个节点的关键字都大于其左子树中任意节点的关键字,小于其右子树中任意节点的关键字。
这种特性使得搜索二叉树非常适合用于查找操作。在搜索二叉树中查找一个元素时,我们可以从根节点开始,如果当前节点的值等于要查找的值,则查找成功;如果当前节点的值大于要查找的值,则在左子树中继续查找;如果当前节点的值小于要查找的值,则在右子树中继续查找.
搜索二叉树还有一些其他的性质,例如:对于一棵有n个节点的搜索二叉树,它的高度不会超过log(n) . 这些性质使得搜索二叉树在计算机科学中有着广泛的应用,例如在数据库索引、编译器符号表等领域。
如下就是一个二叉搜索树:
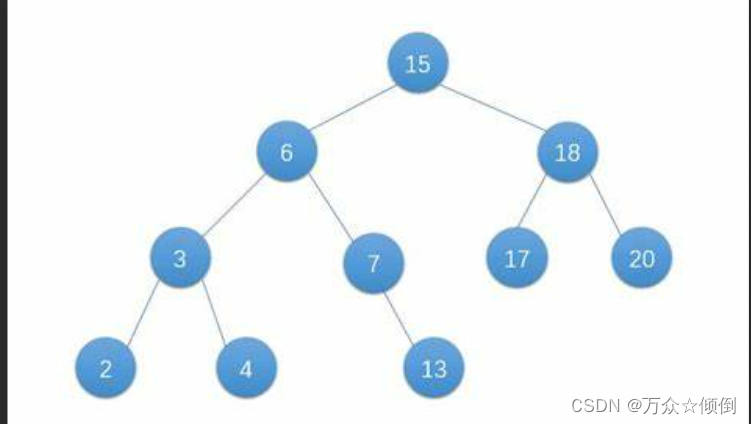
二,搜索二叉树的实现
这里主要指的是实现而二叉树的增删查,搜索二叉树不能被修改。
非递归实现
根据搜索二叉树的特性,实现也是好比较实现的:
到了删除,这个是比较麻烦的,因为我们不能直接删除这个节点,若为叶子节点还好,但凡这个节点但有两个孩子,删除直接会破坏搜索二叉树的结构,那么如何删除。
用如下的搜索二叉树为例:
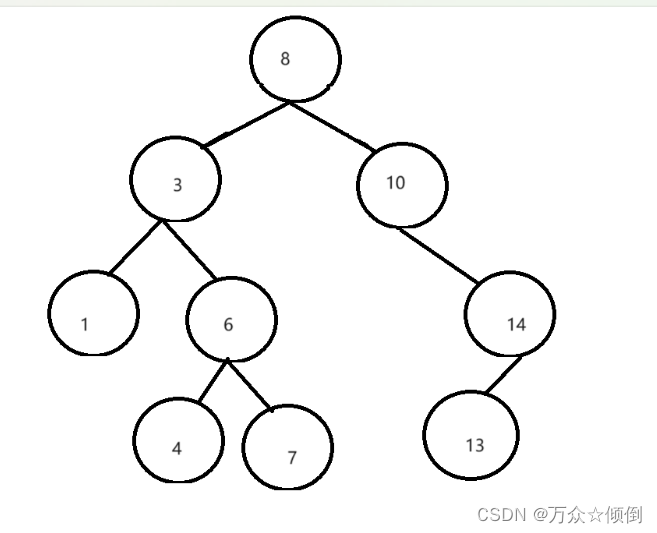
情况一:首先对于叶子节点我们找到后可以直接删除
情况二:删除的节点左子树为空,右子树不为空
如这里的节点10,我们可以将它的孩子托付给它的父亲,即链接8节点的right与14节点,删除节点10。
情况三:删除的节点右子树为空,左子树不为空
情况三与情况四的方法类似,还是用它的父亲节点管理它的孩子节点。
情况四:删除的节点右子树,左子树都不为空
如这里删除节点3,上述思路就不行了。
解决办法:替换法
所谓替换法就是去找一个其他节点来接管我们的孩子,如删除节点3,我么可以看到节点4可以替换3,节点1也可以替换3,虽然他也是这里的子节点,当然节点6理论可以,但它自身也有孩子。
或者删除节点8为例,我们必须要找到一个比8节点左边都大的,且比右边的每个数最小
总结:因此我们可以选择已该节点为起点,它的左子树中最大的节点(左边最大)节点4,右子树中最小(左子树中最右节点)节点7,这两个都可以是我们替换的对象是最为合适的。
节点与类成员
//结点的定义
template<class k>struct BSTreeNOde
{
BSTreeNOde(const k& key) :_left(nullptr),_right(nullptr)
{
this->key = key;
}
BSTreeNOde<k>* _left;
BSTreeNOde<k>* _right;
k key;
};
template<class k>class BSTree
{
public:
typedef BSTreeNOde<k> Node;//搜索二叉树的节点
//成员函数......
private:
Node* _root=nullptr;
}插入
//节点插入
bool insert(const k& key)
{
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (key < cur->key)
{
parent = cur;
cur = cur->_left;
}
else if (key > cur->key)
{
parent = cur;
cur = cur->_right;
}
else
{
//相等就不枉搜索二叉树里插入了
return false;
}
}
//cur为空的时候,即找到了合适的位置,就可以插入了
cur = new Node(key);
//链接
if (key > parent->key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}查找
//查找
bool find(const k key)
{
if (_root == nullptr)
{
return false;
}
Node* cur = _root;
while (cur)
{
if (key > cur->key)
{
cur = cur->_right;
}
else if (key > cur->key)
{
cur = cur->left;
}
else
{
return true;
}
}
return false;
}删除
对于上述分析的情况,情况一就是情况二或情况三的一种,全空可以为左为空或者右为空。
不为空时,我们这里选择替换右子树中的最小值:
对于删除,我们这里断开和删除节点的链接即可,其次对于为空时,我们这里选择替换右子树中的最小值是分两种情况的:当我们的的右子树的第一个节点的左子树是否为空,不为空,我们去一直找最左边的,左子树为空,那么最小的就是第一个右子树节点。
//删除节点
bool Erase(const k& key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (key > cur->key)
{
parent = cur;
cur = cur->_right;
}
else if (key < cur->key)
{
parent = cur;
cur = cur->_left;
}
else
{
//开始删除
//叶子节点可以当作左为空或这右为空处理
//左为空
if (cur->_left == nullptr)
{
//先判断删除的节点是否为根节点
if (cur == _root)
{
//直接用孩子替换为新的根节点
_root = cur->_right;
}
else
{
//直接让它的父亲指向它的右孩子
if (cur == parent->_right)
{
parent->_right = cur->_right;
}
else
{
parent->_left = cur->_right;
}
}
}
else if (cur->_right == nullptr)
//右为空
{
if (cur == _root)
{
//直接用孩子替换为新的根节点
_root = cur->_left;
}
else
{
//直接让它的父亲指向它的右孩子
if (cur == parent->_right)
{
parent->_right = cur->_left;
}
else
{
parent->_left = cur->_left;
}
}
}
//左右都不为空
else
{
//对于这里左子树的最大(最右),右子树的最小(最左)这两个节点都可以被我们所替换
//找右树的最小节点(最左)
Node* subleft = cur->_right;
Node* parent = cur;
if (subleft == nullptr)
{
cur->_left;
}
while (subleft->_left)
{
parent = subleft;
subleft = subleft->_left;
}
swap(cur->key, subleft->key);
//此时subleft的右子树不一定为空 或者 在寻找前此时的左子树整个为空,用他的右子树链接
if (subleft == parent->_left)
{
parent->_left = subleft->_right;
}
else
{
parent->_right = subleft->_right;
}
}
return true;
}
}
return false;
}递归实现
对于增删查,不仅仅可以通过循环,我们也可以通过递归实现
递归实现时,我们可以直接传root的引用,无需用cur来遍历,不过我们需要内部下一个函数来访问到我们的root。利用root的引用,再增加和删除时,递归到该位置我们可直接改变这个节点。
插入
插入的主要过程就是递归左右子树遍历直到此时的root为空,就可插入,return true。否则false。
bool insertR(const k& key)
{
return _insertR(key, _root);
}
bool _insertR(const k& key, Node*& root)
{
if (root == nullptr)
{
//递归直到此时为空,链接
root = new Node(key);
return true;
}
if (root)
{
if (key < root->key)
{
return _insertR(key, root->_left);
}
else if (key > root->key)
{
return _insertR(key, root->_right);
}
else
{
//相等就不往搜索二叉树里插入了
return false;
}
}
}查找
原理同上,递归的左右子树,遍历找我们需要的元素。
bool findR(const k& key)
{
return _findR(_root,key);
}
bool _findR(Node* root, const k& key)
{
if (root == nullptr)
{
return false;
}
if (root->key < key)
{
return _findR(root->_right, key);
}
else if (root->key > key)
{
return _findR(root->_left, key);
}
else
{
return true;
}
}删除
因为循环时无法复用我们在当左子树右子树都不为空时,我们去找右子树的最小值,即右树的最左值,循环右数的左子树的最左直到为空,交换之后,开始删除,我们想要服用左子树为空的删除问题,但此时的父亲不一样,我们不能去服用。
但对于递归,当我们要去找右子树的最左孩子,找到之后交换,然后变成子问题递归,左子树为空删除。
bool EraseR(const k& key)
{
_EraseR(_root, key)
}
bool _EraseR(Node*& root, const k& key)
{
if (root == nullptr)
return false;
if (root->_key < key)
{
return _EraseR(root->_right, key);
}
else if (root->_key > key)
{
return _EraseR(root->_left, key);
}
else
{
// 删除
if (root->_left == nullptr)
{
Node* del = root;
root = root->_right;
delete del;
return true;
}
else if (root->_right == nullptr)
{
Node* del = root;
root = root->_left;
delete del;
return true;
}
else
{
Node* subLeft = root->_right;
while (subLeft->_left)
{
subLeft = subLeft->_left;
}
swap(root->_key, subLeft->_key);
// 转换成在子树去递归删除
return _EraseR(root->_right, key);
}
}