一、引言

在概率计算中，我们常常遇到这样的一类问题，某事件的发生可能依赖于多种原因，对这样的事件直接求规律往往是无能为力的。概率与我们的生存、生活是密不可分的，在我们的生活中要想使我们的期望效用最大化，我们必须考虑各种客观条件的存在，用理性的科学的思维去判断问题、分析问题，最终做出正确的决策。

二、贝叶斯定理

贝叶斯定理（Bayes theorem）是概率论中的一个结果，它跟随机变量的条件概率以及边缘概率分布有关。

通常，事件A在事件B(发生)的条件下的概率，与事件B在事件A的条件下的概率是不一样的；然而，这两者是有确定的关系，贝叶斯定理就是这种关系的陈述。

贝叶斯定理是关于随机事件A和B的条件概率和边缘概率的一则定理。

其中P(A|B)是在B发生的情况下A发生的可能性。
在贝叶斯定理中，每个名词都有约定俗成的名称：
 P(A)是A的先验概率或边缘概率。之所以称为"先验"是因为它不考虑任何B方面的因素。
 P(A|B)是已知B发生后A的条件概率，也由于得自B的取值而被称作A的后验概率。
 P(B|A)是已知A发生后B的条件概率，也由于得自A的取值而被称作B的后验概率。
 P(B)是B的先验概率或边缘概率，也作标准化常量（normalized constant）。

三、先验概率和后验概率

3.1 先验概率

直观理解，所谓“先”，就是在事情之前，即在事情发生之前事情发生的概率。是根据以往经验和分析得到的概率。比如抛硬币，我们都认为正面朝上的概率是0.5，这就是一种先验概率，在抛硬币前，我们只有常识。这个时候事情还没发生，我们进行概率判断。所谓的先验概率是对事情发生可能性猜测的数学表示。

3.2 后验概率

后验概率是事情已经发生了，事情发生可能有很多原因，判断事情发生时由哪个原因引起的概率。

比如今天你没去学校，原因有两个，可能是生病了，也可能是自行车坏了。然后上课时老师发现你没来。（这里是一个结果，就是你没来学校这件事情已经发生了）老师叫学霸计算一下概率，分别是因为生病了没来学校的概率和自行车坏了没来学校的概率。

很显然，后验概率就是在事情发生后判断由哪一个原因引起的概率。这里的事情是你上学迟到，原因有生病了和自行车坏了。

数学表达：

四、最大后验准则

在对一个物体进行分类时，最直观的方法是根据这个物体的特征，选择最契合这个特征的类，这种思想就是最大化后验准则。形式化地描述就是根据某个物体的特征向量x，估计每个类在这特征向量下的后验概率，然后选择后验概率最大的类。

P(x)和P(w)作为先验概率。如果我们没有先验知识，只能忽略掉先验，这时候决策准则就变成了最大似然(Maximum Likelihood，ML)准则：

最大似然准则一个的直观理解是在什么样的状态下，最可能产生现在的观测到的数据。

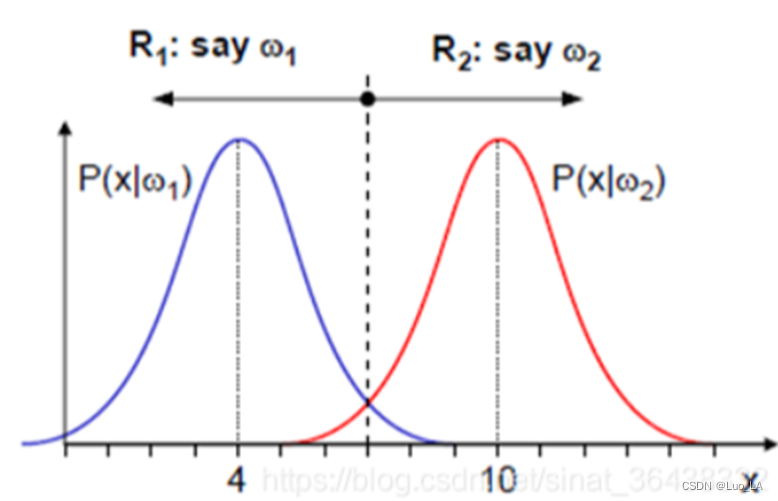
假设我们需要设计一个能分开鲈鱼和鲑鱼的分类器(约定w_1代表鲑鱼，w_2代表鲈鱼)。当我们唯一能利用的信息是先验概率时，即只知道鲈鱼和鲑鱼的出现概率P(w_1)和P(w_2)，那么我们就按照以下准则判断：若P(w_1)>P(w_2)就判定为w1，反之亦然。

如果只进行一次判决，这样的准则还是合理的，但是如果我们需要多次进行判断，那这样判断就很奇怪。好在大多数情况下，我们不会只根据先验进行判断，假设我们已经统计出了鲈鱼和鲑鱼身长的概率：

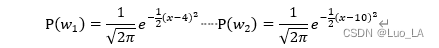
那么，在进行判断时，我们可以根据鱼的身长x最大化P(x|w)判断属于哪一类，如下图，这样就是最大似然准则。

五、最小错误率

最小错误率决策指将样本分错的概率最小，换句话说就是在对样本进行分类的时候分为正确类别的概率最大。也就是说，把使得后验概率p(wi|x)最大的wi作为x的判定类别。因为p(wi|x)最大即表示x属于wi的概率最大，也就是x被判错的概率最小。

决策的好坏可以通过错误率进行衡量，错误率可以根据全概率公式总合每个类分错的概率和这个类的概率，下面的公式很直观地解释了错误率。

其中，P[error|w]是类被分错的概率，所谓分错就是被分成了其他类。
以上面鲑鱼、鲈鱼分类为例，我们根据最大似然准则确定了对鲈鱼和鲑鱼的分类。直观上，错误率就如下图的阴影部分：

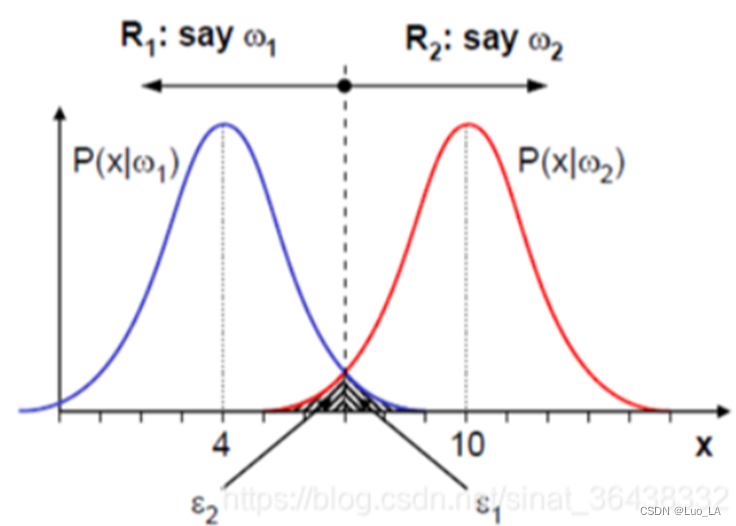
公式表示为：

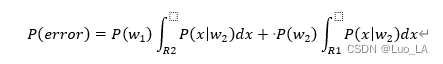
其中，对P[x|w1]在R2决策区域的积分就是w1被错分为w2的概率，对应阴影部分ε1。
上面的错误率是在每个类别的分布(即先验)已知的状态下计算的。我们也可以根据全概率公式综合所有样本计算错误率：

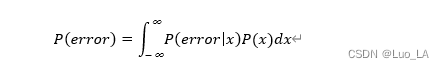
对于最大后验准则，我们选择P(w|x)最大的决策。直观上，某类后验概率的最大化对应着其他类的后验概率之和最小化，也就是P[error|x]的最小化，而P(x)是固定的，所以直观上最大后验概率准则最小化了错误率。

六、最小化风险

最大化后验准则假设每类分错时代价(或者说惩罚)是一样的。然而在实际生活中，往往没有这么理想，如疾病诊断时把实际有病的人分类为健康的代价就比把健康的人分类为有病的代价大。贝叶斯准则就是考虑了误分类带来的不同的风险，最小化风险进行分类。定义贝叶斯风险如下：

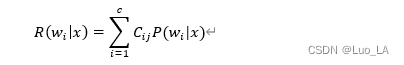
其中，C_ij表示将j类错分为i类导致的代价，代价乘以该类的概率就是将该类错分为i类的风险。因此分类为i类的贝叶斯风险就是将其他类错分为i类的风险总合。我们在决策时，选择的是贝叶斯风险最小的类。
可以发现，当C_ij是如下形式时，贝叶斯准则就成为了最大后验准则：

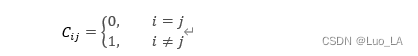
因此，最大后验准则是贝叶斯准则的一个特定情况，最大似然准则是最大后验准则的一个特定情况。
与最大后验准则最小化的错误率相对应，贝叶斯准则最小化的是贝叶斯风险。

七、最小最大决策

从最小错误率和最小风险贝叶斯决策中可以看出其决策都是与先验概率P(w_i)有关的。如果给定的x，其P(w_i)不变，按照贝叶斯决策规则，可以使错误率和风险最小。但是如果P(w_i)是可变的，或事先对先验概率毫不知道的情况下，若再按某个固定的P(w_i)条件下的决策进行就往往得不到最小错误率或最小风险。而最小最大决策就是考虑在P(w_i)变化的情况下，如何使最大可能的风险为最小，也就是在最差的条件下争取到最好的结果。

在做最小最大贝叶斯决策时，若考虑P(w_i)有可能改变或对先验概率毫不知晓的情况下，应选择贝叶斯风险R为最大值时的P(w_i)来设计分类器，此时能保证其风险相对于其它的P(w_i)为最大，而能保证在不管P(w_i)如何变化，使最大最小风险为最小。

八、贝叶斯决策建模

1. 确定决策问题的状态空间和决策空间；
2. 确定各状态的先验概率分布；
3. 确定各状态下各决策的条件概率分布；
4. 计算各决策的期望损失，并选择期望损失最小的决策。

参考

http://t.csdnimg.cn/lrdGp
http://t.csdnimg.cn/3LNPF