先做个简单的笔记整理，以后有时间再补上细节

优先级采样

均匀随机采样（uniformly sampling）会使得部分采样的结果对实际的更新毫无作用。如下图所示，在开始时，只有靠近终点部分的更新会产生作用，而其他情况则不会。因此，模拟的经验和更新应集中在一些特殊的状态动作。

可以使用后向聚焦（backward focusing）进行更好地更新。 后向聚焦是指很多状态的值发生变化带动前继状态的值发生变化。但有的值改变很多，有的改变很少，因此需要根据紧急程度，给这些更新设置优先度进行更新。

优先级采样（Prioritized Sweeping）可以解决上述问题。优先级采样通过设置优先级更新队列，根据值改变的幅度定义优先级：$$P\leftarrow \left|R+\gamma \underset{a}{\max }Q\left(S^{\prime },a\right)-Q(S,A)\right|$$

算法伪代码：

Example1 Prioritized Sweepingon Mazes

• 横轴代表格子世界的大小
• 纵轴代表收敛到最优策略的更新次数
• 优先级采样收敛更快

局限性及改进

优先级采样在随机环境中利用期望更新（expected updates）的方法。但这样会浪费很多计算资源在一些低概率的状态转移（transitions）上，因此引入采样更新（sample updates）。

期望更新和采样更新

期望更新

• $$Q(s,a)\leftarrow \sum _{s^{\prime },r}\hat{p}(s^{\prime },r|s,a)[r+\gamma \underset{a^{\prime }}{\max }Q(s^{\prime },a^{\prime })].$$
• 需要知道准确的分布模型
• 需要更大的计算量
• 没有偏差更准确

采样更新

• $$Q(s,a)\leftarrow Q(s,a)+\alpha [R+\gamma \underset{a^{\prime }}{\max }Q(S^{\prime },a^{\prime })-Q(s,a)],$$ • 只需要采样模型
  • 计算量需求更低
  • 受到采样误差(sampling error)的影响

不同分支因子下的表现

设定
• 𝑏 个后续状态等可能
• 初始估计误差为1
• 下一个状态值假设估计正确

结果
• 分支因子越多，采样更新越接近期望更新
• 大的随机分支因子和状态数量较多的情况下, 采样更新更好

越复杂的环境越适合进行采样更新。

轨迹采样

• 动态规划
  • 对整个状态空间进行遍历
  • 没有侧重实际需要关注的状态上
• 在状态空间中按照特定分布采样
  • 根据当前策略下所观测的分布进行采样

轨迹采样

• 状态转移和奖励由模型决定
• 动作由当前的策略决定

优点
• 不需要知道当前策略下状态的分布
• 计算量少，简单有效
缺点
• 不断重复更新已经被访问的状态

• 不同的分支因子下的表现
• 确定性环境中表现比较好

总结

• 优先级采样
  • 收敛更快
  • 随机环境使用期望更新，计算量大
• 期望更新和采样更新
  • 期望更新计算量大但是没有偏差
  • 采样更新计算量小但是存在采样偏差
• 轨迹采样
  • 采样更新，计算量小
  • 不断重复某些访问过的状态

实时动态规划

和传统动态规划的区别
• 实时的轨迹采样
• 只更新轨迹访问的状态值

优势
• 能够跳过策略无关的状态
• 在解决状态集合规模大的问题上具有优势
• 满足一定条件下可以以概率1收敛到最优策略

Example2 racetrack

决策时规划

背景规划（Background Planning）
• 规划是为了更新很多状态值供后续动作的选择
• 如动态规划，Dyna

决策时规划（Decision-time Planning）
• 规划只着眼于当前状态的动作选择
• 在不需要快速反应的应用中很有效，如棋类游戏

启发式搜索

• 访问到当前状态(根节点)，对后续可能的情况进行树结构展开

• 叶节点代表估计的值函数

• 回溯到当前状态(根节点)，方式类似于值函数的更新方式
  

• 决策时规划，着重于当前状态

• 贪婪策略在单步情况下的扩展

• 启发式搜索看多步规划下，当前状态的最优行动

• 搜索越深，计算量越大，得到的动作越接近最优

• 性能提升不是源于多步更新，而是源于专注当前状态的后续可能

Rollout算法

• 从当前状态进行模拟的蒙特卡洛估计
• 选取最高估计值的动作
• 在下一个状态重复上述步骤

特点

• 决策时规划，从当前状态进行𝑟𝑜𝑙𝑙𝑜𝑢𝑡
• 直接目的类似于策略迭代和改进，寻找更优的策略
• 表现取决于蒙特卡洛方法估值的准确性

蒙特卡洛树搜索

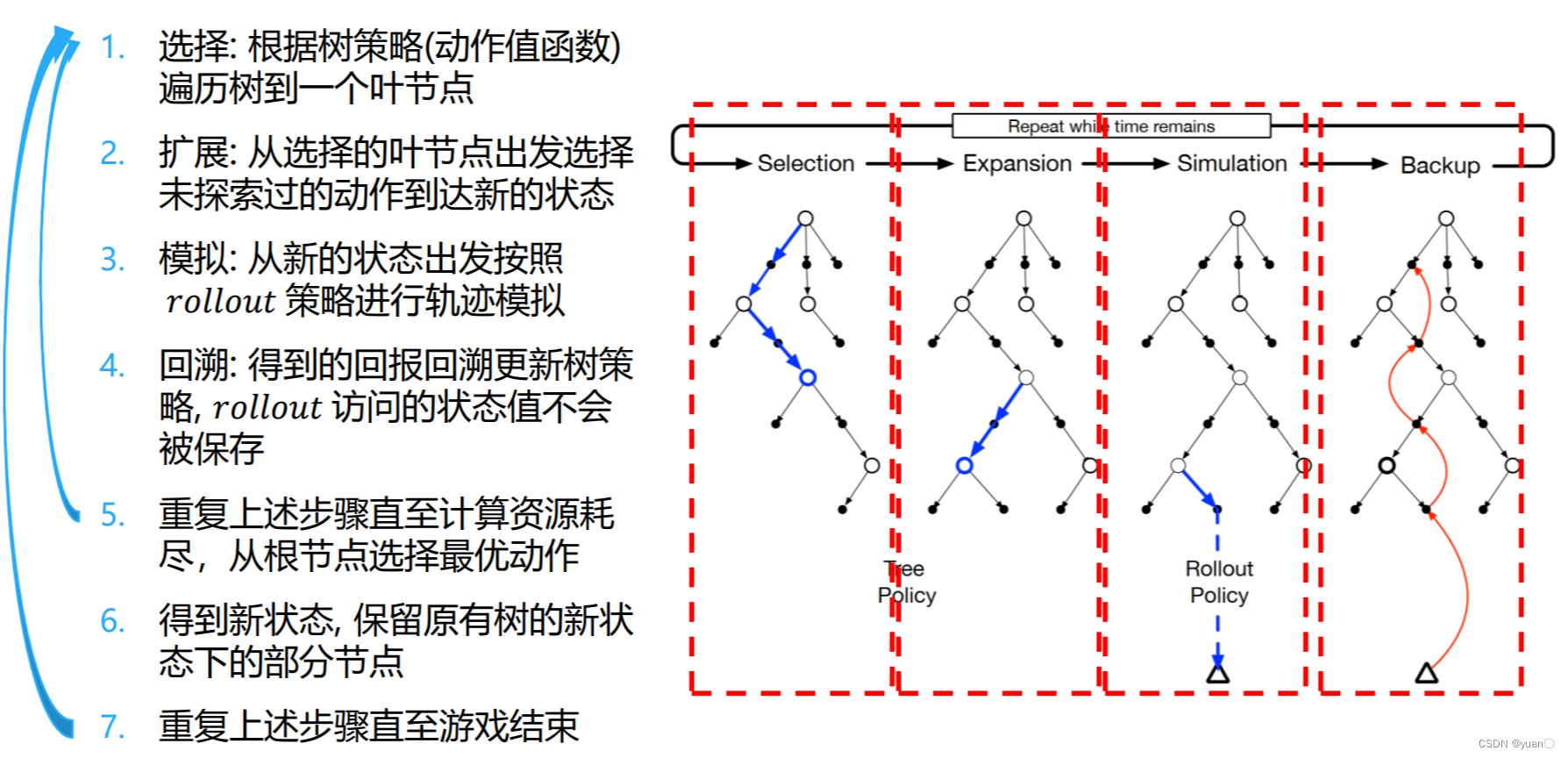
参考

[1] 伯禹AI
[2] https://www.deepmind.com/learning-resources/introduction-to-reinforcement-learning-with-david-silver
[3] 动手学强化学习
[4] Reinforcement Learning