目录
适用于多项式模型的 MATLAB 函数
带非多项式项的线性模型
多次回归
适用于多项式模型的 MATLAB 函数
有两个 MATLAB® 函数可通过多项式对数据建模。
多项式拟合函数
| 函数 | 说明 |
|---|---|
| polyfit | polyfit(x,y,n) 通过最大限度地减小数据与模型偏差的平方和(最小二乘拟合),求拟合 y 数据的 n 次多项式 p(x) 的系数。 |
| polyval | polyval(p,x) 返回基于 x 进行计算,且由 polyfit 确定的 n 次多项式的值。 |
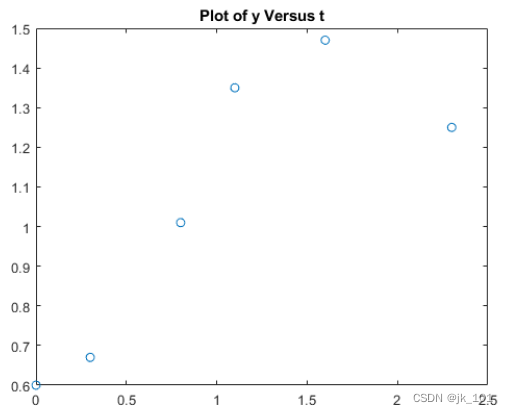
此示例说明如何使用多项式对数据建模。在时间 t 的多个值处测量数量 y。
t = [0 0.3 0.8 1.1 1.6 2.3];
y = [0.6 0.67 1.01 1.35 1.47 1.25];
plot(t,y,'o')
title('Plot of y Versus t')如图所示:
可尝试使用以下二次多项式函数对此数据进行建模:
![]()
通过最大限度地减小数据与模型偏差的平方和(最小二乘拟合),计算未知系数 a0、a1和a2
使用 polyfit 求多项式系数。
p = polyfit(t,y,2)
p = 1×3
-0.2942 1.0231 0.4981MATLAB 以降幂计算多项式系数。数据的二次多项式模型由以下方程给出:
![]()
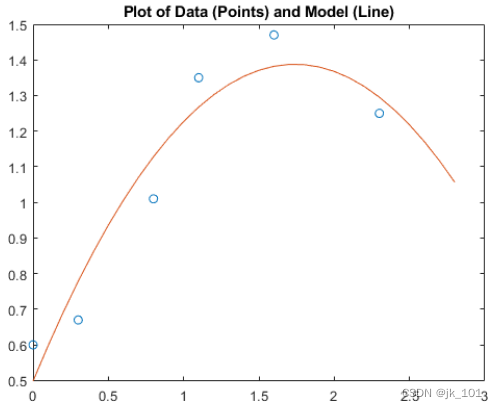
按均匀的时间间隔 t2 计算多项式。然后,在同一个图中绘制原始数据和模型。
t2 = 0:0.1:2.8;
y2 = polyval(p,t2);
figure
plot(t,y,'o',t2,y2)
title('Plot of Data (Points) and Model (Line)')如图所示:
按数据时间向量计算模型
y2 = polyval(p,t);计算残差。
res = y - y2;绘制残差图。
figure, plot(t,res,'+')
title('Plot of the Residuals')如图所示:
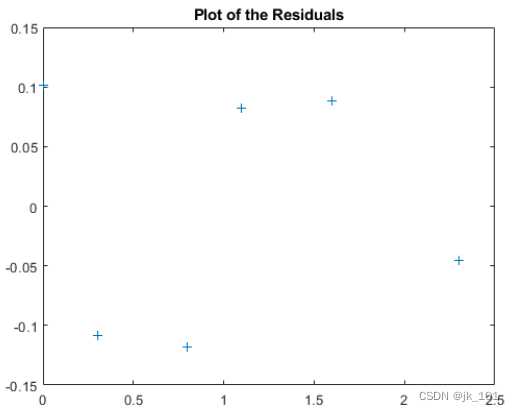
请注意,二阶拟合大致遵循数据的基本形状,但并不能捕获数据似乎具备的平滑曲线。残差似乎存在一个模式,意味着可能需要不同的模型。如下所示,五次多项式在遵循数据波动方面表现更佳。
重复该练习,不过这次使用来自 polyfit 的五次多项式。
p5 = polyfit(t,y,5)
p5 = 1×6
0.7303 -3.5892 5.4281 -2.5175 0.5910 0.6000
在 t2 上计算多项式,并在新的图窗窗口中基于数据绘制拟合图。
y3 = polyval(p5,t2);
figure
plot(t,y,'o',t2,y3)
title('Fifth-Degree Polynomial Fit')如图所示:
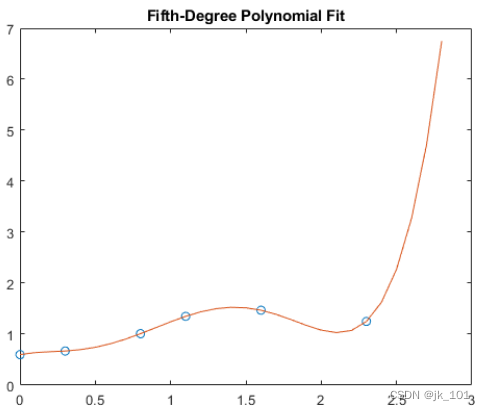
注意:如果尝试对物理情况建模,务必考虑特定阶次的模型是否对您的情况有意义。
带非多项式项的线性模型
此示例说明如何使用含有非多项式项的线性模型拟合数据。若多项式函数并未得出适合您数据的满意模型,可尝试使用带非多项式项的线性模型。以如下函数为例,它在参数 a0、a1 和 a2 中为线性,而在 t 数据中为非线性:
![]()
可通过构建及求解一组联立方程并为参数求解,计算未知系数 a0、a1 和 a2。以下语法通过构建一个设计矩阵实现此目的,该矩阵中的每一列代表用于预测响应(模型中的项)的变量,每一行对应于这些变量的一个观测值。输入 t 和 y 作为列向量。
t = [0 0.3 0.8 1.1 1.6 2.3]';
y = [0.6 0.67 1.01 1.35 1.47 1.25]';构建设计矩阵。
X = [ones(size(t)) exp(-t) t.*exp(-t)];计算模型系数。
a = X\y
a = 3×1
1.3983
-0.8860
0.3085
因此,该数据的模型由以下公式提供:
![]()
现在以等间距点评估模型,并以原始数据绘制模型。
T = (0:0.1:2.5)';
Y = [ones(size(T)) exp(-T) T.*exp(-T)]*a;
plot(T,Y,'-',t,y,'o'), grid on
title('Plot of Model and Original Data')如图所示:
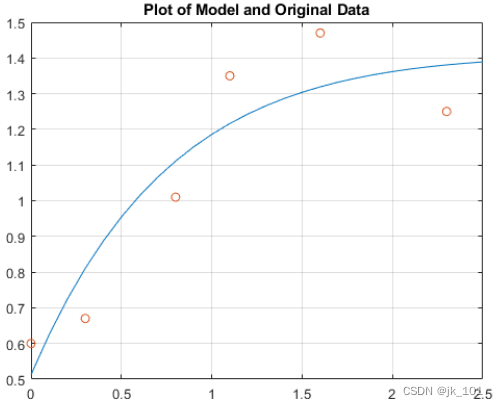
多次回归
此示例说明如何使用多次回归对具有多个预测变量的函数进行数据建模。若 y 是具有多个预测变量的函数,则必须对表示各变量之间关系的矩阵方程进行扩展,以容纳额外的数据。这称为多次回归。
为多个 x1 和 x2 值测量对应的量 y。将这些值分别存储在向量 x1、x2 和 y 中。
x1 = [.2 .5 .6 .8 1.0 1.1]';
x2 = [.1 .3 .4 .9 1.1 1.4]';
y = [.17 .26 .28 .23 .27 .24]';此数据的模型采用以下形式:
![]()
多次回归可通过最大限度地减小数据与模型偏差的平方和(最小二乘拟合),对未知系数 a0、a1 和 a2 求解。
通过构建设计矩阵 X,构建和求解一组联立方程。
X = [ones(size(x1)) x1 x2];使用反斜杠运算符对参数求解。
a = X\y
a = 3×1
0.1018
0.4844
-0.2847数据的最小二乘拟合模型为
![]()
为了验证该模型,请求出数据与模型偏差绝对值的最大值。
Y = X*a;
MaxErr = max(abs(Y - y))
MaxErr = 0.0038该值远小于任何数据值,表明该模型能够准确贴合数据。