弗洛伊德算法,也称为迪科斯彻算法,是一种用于寻找图形中所有最短路径的算法。它的基本思想是通过一定的规则逐步更新每个节点的最短路径估计值,直到每个节点的最短路径估计值收敛为止。
具体来说,弗洛伊德算法通过求解所有点对之间的最短路径来实现。在算法开始时,我们假设图中的所有节点之间都是不联通的,即它们之间的距离为无穷大。然后,我们对图进行“松弛”操作,即尝试更新每个节点之间的距离估计值,以寻找更短的路径。具体来说,对于图中的每个节点对(i,j),我们检查是否存在一个节点k,使得从i到k再到j的路径比已知的最短路径更短。如果是的话,我们就更新(i,j)之间的距离估计值为更短的路径长度。
通过重复这个过程,我们最终得到了图中所有节点之间的最短路径估计值。弗洛伊德算法的时间复杂度为O(n^3),其中n是图中节点的数量。

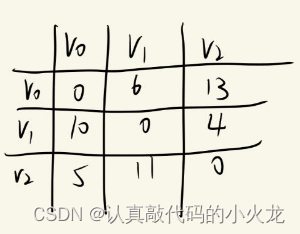
邻接矩阵为

弗洛伊德算法
每次都选一个顶点作为中转点
第一次将V0作为中转点
对所有顶点i,j做判断dist[i][j]>dist[i][k]+dist[k][j] (k为此时的中转点)
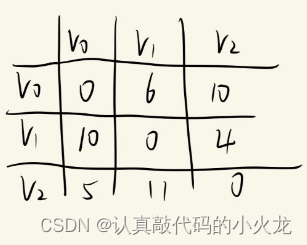
第二次将V1作为中转点
再次对所有顶点i,j做判断dist[i][j]>dist[i][k]+dist[k][j] (k为此时的中转点)
第三次将V2作为中转点
对所有顶点i,j做判断dist[i][j]>dist[i][k]+dist[k][j] (k为此时的中转点)
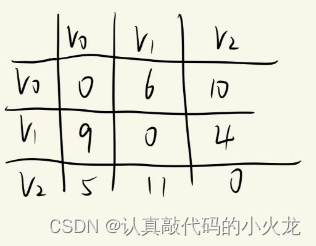
就得到了最终结果
下面我们来看一下代码是如何实现的(c语言代码实现)
void floyd(int graph[n][n])//弗洛伊德求各顶点之间的最短路径
{
int dist[n][n];
for (int i = 0; i < n; i++)//初始化距离矩阵
{
for (int j = 0; j < n; j++)
dist[i][j] = graph[i][j];
}
for (int k = 0; k < n; k++)//逐一考虑每个顶点作为中间顶点
{
for (int i = 0; i < n; i++)//
{
for (int j = 0; j < n; j++)
{
if (dist[i][j] > dist[i][k] + dist[k][j])//k作为中间顶点,可以缩短(i,j)的距离
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
if (dist[i][j] != Max)
printf("%d\t", dist[i][j]);
else
printf("Max");
}
printf("\n");
}
}完整测试代码
#include<stdio.h>
#define Max 0xFFFF
#define n 3
void floyd(int graph[n][n])//弗洛伊德求各顶点之间的最短路径
{
int dist[n][n];
for (int i = 0; i < n; i++)//初始化距离矩阵
{
for (int j = 0; j < n; j++)
dist[i][j] = graph[i][j];
}
for (int k = 0; k < n; k++)//逐一考虑每个顶点作为中间顶点
{
for (int i = 0; i < n; i++)//
{
for (int j = 0; j < n; j++)
{
if (dist[i][j] > dist[i][k] + dist[k][j])//k作为中间顶点,可以缩短(i,j)的距离
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
if (dist[i][j] != Max)
printf("%d\t", dist[i][j]);
else
printf("Max");
}
printf("\n");
}
}
int main()
{
int graph[n][n] = { {0,6,13},{10,0,4} ,{5,Max,0} };
floyd(graph);
return 0;
}