题目描述：

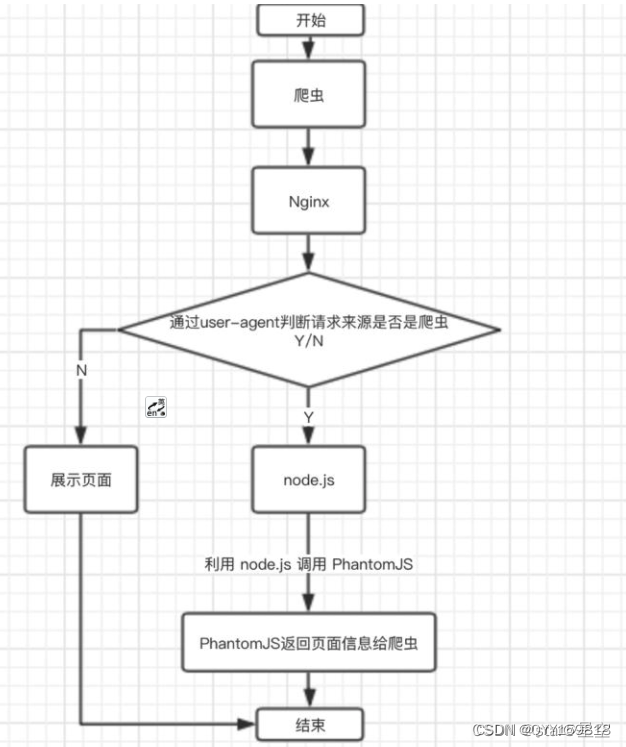
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

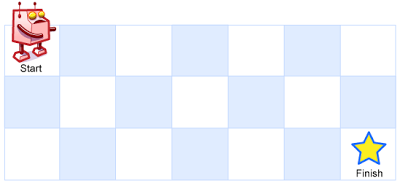
输入：m = 3, n = 7
输出：28

示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3
输出：28

示例 4：

输入：m = 3, n = 3
输出：6

提示：

• 1 <= m, n <= 100
• 题目数据保证答案小于等于 2 * 109

通过次数

687.6K

提交次数

1M

通过率

67.9%

方法一、动态规划

机器人要是想走到第一排或第一列，只能由起点一直向左走或向右走，即路径数量为1。

机器人要是想走到除第一排或第一列的某个位置，假设坐标为（i，j），那么机器人必须经过坐标（i-1,j）或坐标（i,j-1）。

如果有dp[i][j]表示机器人走到(i,j)位置路径数量则i==1||j==1时，dp[i][j]=1；其余情况dp[i][j]=dp[i-1][j]+dp[i][j-1]。dp[m][n]即为所求答案。

上述算法有两种写法

一、递归。（写起来方便，数据大时会超时）

class Solution{
public:
    int uniquePaths(int m,int n)
    {
        if(m==1||n==1) return 1;
        else return uniquePaths(m-1,n)+uniquePaths(m,n-1);
    }
};

二、动态规划。（不用嵌套调用，不会超时）

class Solution {
public:
    int uniquePaths(int m, int n) {
        int dp[101][101];
        for(int i=1;i<=n;i++)
        {
            dp[1][i]=1;
        }
        for(int i=2;i<=m;i++)
        {
            dp[i][1]=1;
            for(int j=2;j<=n;j++)
            {
                dp[i][j]=dp[i-1][j]+dp[i][j-1];
            }
        }
        return dp[m][n];
    }
};

方法二：排列组合

这题给高中生30s做出来。就是一共要走m+n-2步骤，其中有m-1步是向下走，另外n-1步是向右走。所以最后答案就是C  。即( (m+n-2)*(m+n-3)*......*(n) )/( (m-1)*(m-2)*......*(1) )，用m-1次的循环就完成了。

class Solution{
public:
    int uniquePaths(int m,int n)
    {
        long long ans=1;
        if(m==1||n==1) return 1;
        int x=n,y=1;
        for(int i=0;i<m-1;i++)
        {
            ans=ans*x/y;
            x++;
            y++;
        }
        return ans;
    }
};