4.1 数组

4.1.1 数组的存储和寻址

  数组是一种用于存储多个相同类型元素的数据结构。在内存中，数组的元素是连续存储的，可以通过下标来寻址和访问特定的元素。数组的存储通常是基于某种固定的数据类型，例如整数数组、字符数组等。关于数组的基础知识可参考前文：
【重拾C语言】六、批量数据组织（一）数组（数组类型、声明与操作、多维数组）

4.1.2 一维数组的基本操作

  一维数组的基本操作包括创建数组、访问数组元素、修改数组元素、插入元素、删除元素等。创建数组时需要指定数组的大小，然后可以使用索引来访问和修改数组中的元素。插入和删除元素通常移动其他元素以保持数组的连续性。

#include <stdio.h>

int main() {
    // 创建数组并初始化
    int array[5] = {1, 2, 3, 4, 5};

    // 访问数组元素
    int element = array[2];
    printf("访问数组中的第三个元素：%d\n", element);

    // 修改数组元素
    array[0] = 10;
    printf("修改数组中的第一个元素为：%d\n", array[0]);

    // 插入元素
    int newSize = 6;
    int position = 2;
    int newValue = 7;

    // 移动元素
    for (int i = newSize - 1; i > position; i--) {
        array[i] = array[i - 1];
    }

    // 插入新元素
    array[position] = newValue;
    newSize++;

    // 打印插入元素后的数组
    printf("插入元素后的数组：");
    for (int i = 0; i < newSize; i++) {
        printf("%d ", array[i]);
    }
    printf("\n");

    // 删除元素
    int deletePosition = 3;

    // 移动元素
    for (int i = deletePosition; i < newSize - 1; i++) {
        array[i] = array[i + 1];
    }
    newSize--;

    // 打印删除元素后的数组
    printf("删除元素后的数组：");
    for (int i = 0; i < newSize; i++) {
        printf("%d ", array[i]);
    }
    printf("\n");

    return 0;
}

输出：

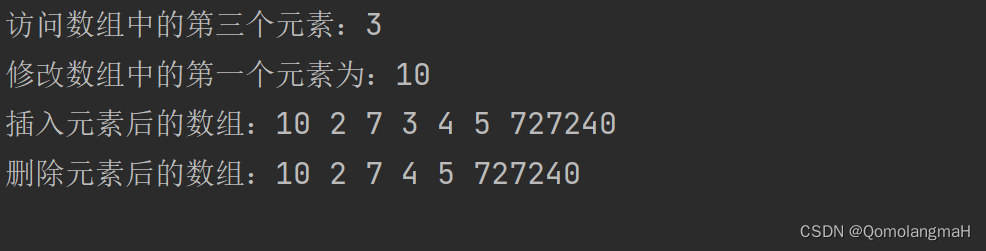
  如上述结果所示，为数组提供越界索引保护是十分必要。在很多高级程序设计语言提供的数组类型没有越界索引保护，不检查数组的下标是否合法，如果索引越界且程序尝试访问由索引指定的元素，则可能访问任何随机内存位置中存放的数据。

4.2 矩阵

4.2.1 矩阵的数组表示

  矩阵是许多物理问题中出现的数学对象，是一种常用的数据组织方式。计算机工作者关心的是矩阵在计算机中如何存储，以及如何实现矩阵的基本操作。
  很自然会想到用二维数组存放矩阵，这也是矩阵存储的一个重要直观方法。此外，由前文可知，高级程序设计语言的二维数组采用按行优先次序顺序存储，因此也可以用一维数组来存放矩阵元素，存放次序是按行优先。换句话说，用规模为m×n的一维数组B来存放m行n列的二维矩阵A，且A中元素aij (1≤ i≤ m, 1 ≤ j ≤ n) 应存放在B[(i-1)×n+j-1] 处。
  数组的基本操作是数组加减，而矩阵的基本操作还有矩阵相乘和矩阵转置等。下面以矩阵乘法为例介绍矩阵的基本操作。矩阵的乘法运算略为复杂，对于矩阵Am×p和Bp×n的乘积Cm×n ，其第i行第j列元素cij的计算公式为 cij = Σ(ai1 * b1j + ai2 * b2j + … + aip * bpj)

a. 矩阵的二维数组存储及其乘法运算

#include <stdio.h>

void matrix_multiply(int A[][3], int B[][2], int C[][2], int m, int p, int n) {
    int i, j, k;
    
    for (i = 0; i < m; i++) {
        for (j = 0; j < n; j++) {
            C[i][j] = 0;
            for (k = 0; k < p; k++) {
                C[i][j] += A[i][k] * B[k][j];
            }
        }
    }
}

void print_matrix(int matrix[][2], int rows, int cols) {
    int i, j;
    
    for (i = 0; i < rows; i++) {
        for (j = 0; j < cols; j++) {
            printf("%d ", matrix[i][j]);
        }
        printf("\n");
    }
}

int main() {
    int A[2][3] = {{1, 2, 3},
                   {4, 5, 6}};
    int B[3][2] = {{7, 8},
                   {9, 10},
                   {11, 12}};
    int C[2][2];
    
    int m = 2;  // A的行数
    int p = 3;  // A的列数 / B的行数
    int n = 2;  // B的列数
    
    matrix_multiply(A, B, C, m, p, n);
    
    printf("Result:\n");
    print_matrix(C, m, n);
    
    return 0;
}

• matrix_multiply的函数接受三个二维数组作为参数：A，B和C，以及三个整数m，p和n。
  • 这些参数分别表示矩阵A的行数、矩阵A的列数（也是矩阵B的行数），以及矩阵B的列数。
  • 使用三个嵌套的循环来计算矩阵乘法：
    • 外层的两个循环变量i和j分别用于遍历结果矩阵C的行和列。
    • 在每次迭代中，将矩阵C的当前元素初始化为0。
    • 然后，通过内层的循环变量k来遍历矩阵A的列和矩阵B的行，并将对应元素相乘并累加到矩阵C的当前元素上。

输出：

b. 一维数组存储

#include <stdio.h>

void flattenMatrix(int matrix[][3], int rows, int columns, int array[]) {
    int index = 0;
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < columns; j++) {
            array[index] = matrix[i][j];
            index++;
        }
    }
}

int main() {
    int matrix[3][3] = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};
    int rows = 3;
    int columns = 3;
    int array[rows * columns];

    flattenMatrix(matrix, rows, columns, array);

    // 输出一维数组
    for (int i = 0; i < rows * columns; i++) {
        printf("%d ", array[i]);
    }

    return 0;
}