最近XGboost支持分位数回归了,我看了一下,就做了个小的代码案例。毕竟学术市场上做这种新颖的机器学习和传统统计学结合的方法还是不多,算的上创新,找个好数据集可以发论文。
代码实现
导入包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error,r2_score
import xgboost as xgb
import lightgbm as lgb
import statsmodels.api as sm
from statsmodels.regression.quantile_regression import QuantRegxgboost和lightgbm都需要安装的,他们和sklearn库的机器学习方法不是一个库的。怎么安装看我《实用的机器学习》这个栏目的xgb那篇文章。
模拟数据进行分位数回归
先制作一个模拟数据集
def f(x: np.ndarray) -> np.ndarray:
return x * np.sin(x)
rng = np.random.RandomState(2023)
X = np.atleast_2d(rng.uniform(0, 10.0, size=1000)).T
expected_y = f(X).ravel()
sigma = 0.5 + X.ravel() / 10.0
noise = rng.lognormal(sigma=sigma) - np.exp(sigma**2.0 / 2.0)
y = expected_y + noise
print(X.shape,y.shape)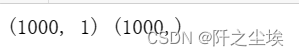
然后画图看看:
plt.figure(figsize=(6,2),dpi=100)
plt.scatter(X,y,s=1)
plt.show()
#划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=rng)
print(f"Training data shape: {X_train.shape}, Testing data shape: {X_test.shape}")
这里采用三种模型进行拟合预测对比,分别是线性分位数回归,XGB结合分位数,LightGBM结合分位数:
alphas = np.arange(5, 100, 5) / 100.0
print(alphas)
mse_qr, mse_xgb, mse_lgb = [], [], []
r2_qr, r2_xgb, r2_lgb = [], [], []
qr_pred,xgb_pred,lgb_pred={},{},{}
# Train and evaluate
for alpha in alphas:
# Quantile Regression
model_qr = QuantReg(y_train, sm.add_constant(X_train)).fit(q=alpha)
model_pred=model_qr.predict(sm.add_constant(X_test))
mse_qr.append(mean_squared_error(y_test,model_pred ))
r2_qr.append(r2_score(y_test,model_pred))
# XGBoost
model_xgb = xgb.train({"objective": "reg:quantileerror", 'quantile_alpha': alpha},
xgb.QuantileDMatrix(X_train, y_train), num_boost_round=100)
model_pred=model_xgb.predict(xgb.DMatrix(X_test))
mse_xgb.append(mean_squared_error(y_test,model_pred ))
r2_xgb.append(r2_score(y_test,model_pred))
# LightGBM
model_lgb = lgb.train({'objective': 'quantile', 'alpha': alpha,'force_col_wise': True,},
lgb.Dataset(X_train, y_train), num_boost_round=100)
model_pred=model_lgb.predict(X_test)
mse_lgb.append(mean_squared_error(y_test,model_pred))
r2_lgb.append(r2_score(y_test,model_pred))
if alpha in [0.1,0.5,0.9]:
qr_pred[alpha]=model_qr.predict(sm.add_constant(X_test))
xgb_pred[alpha]=model_xgb.predict(xgb.DMatrix(X_test))
lgb_pred[alpha]=model_lgb.predict(X_test)分位点为0.1,0.5,0.9时记录一下,方便画图查看。
然后画出三种模型在不同分位点下的误差和拟合优度对比:
plt.figure(figsize=(7, 5),dpi=128)
plt.subplot(211)
plt.plot(alphas, mse_qr, label='Quantile Regression')
plt.plot(alphas, mse_xgb, label='XGBoost')
plt.plot(alphas, mse_lgb, label='LightGBM')
plt.legend()
plt.xlabel('Quantile')
plt.ylabel('MSE')
plt.title('MSE across different quantiles')
plt.subplot(212)
plt.plot(alphas, r2_qr, label='Quantile Regression')
plt.plot(alphas, r2_xgb, label='XGBoost')
plt.plot(alphas, r2_lgb, label='LightGBM')
plt.legend()
plt.xlabel('Quantile')
plt.ylabel('$R^2$')
plt.title('$R^2$ across different quantiles')
plt.tight_layout()
plt.show()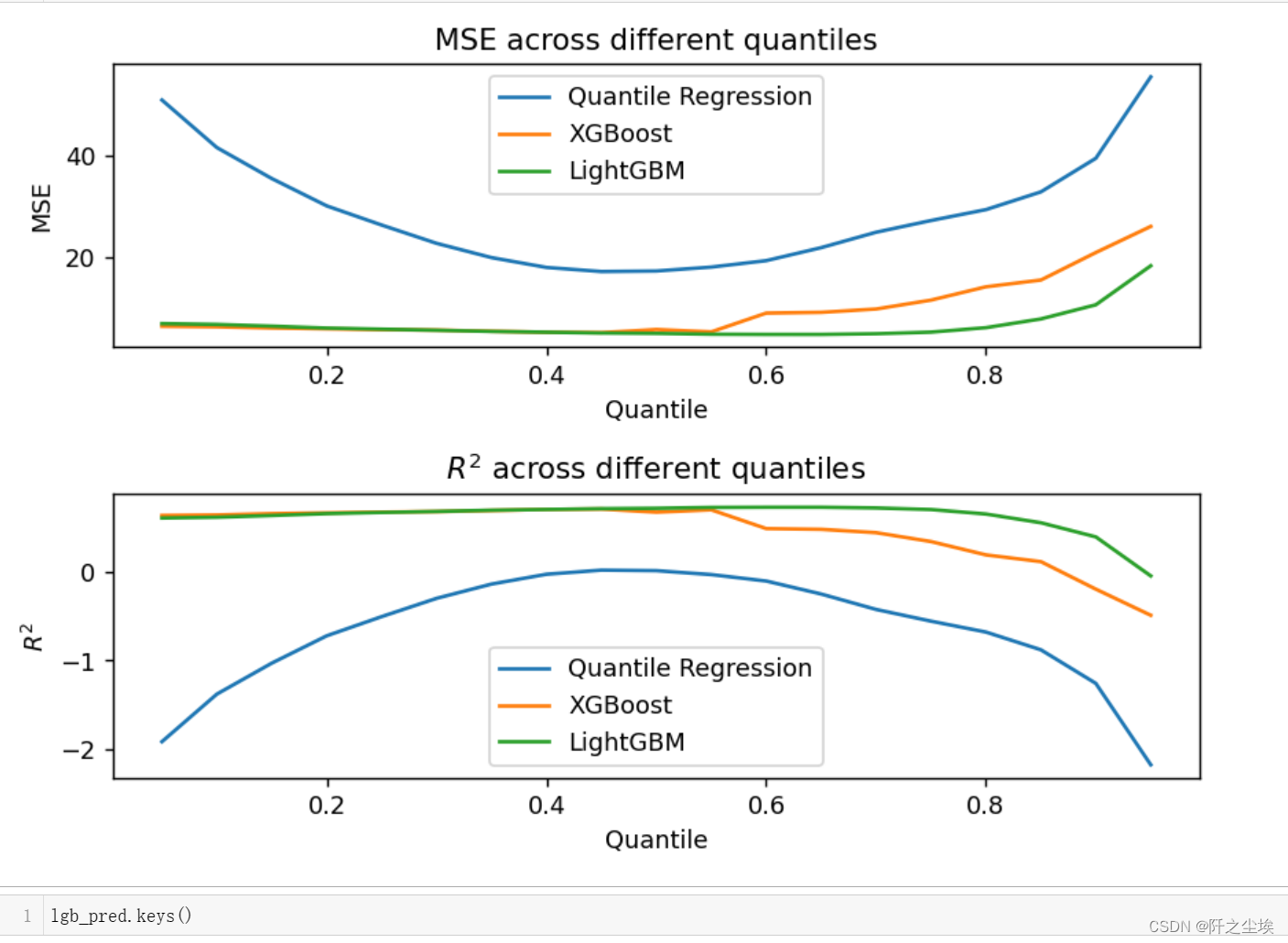
可以看到在分位点为0.5附件,模型的误差都比较小。因为这个数据集没有很多的异常值。然后模型表现上,LGBM>XGB>线性QR。线性模型对于一个非线性的函数关系拟合在这里当然不行。
画出拟合图:
name=['QR','XGB-QR','LGB-QR']
plt.figure(figsize=(7, 6),dpi=128)
for k,model in enumerate([qr_pred,xgb_pred,lgb_pred]):
n=int(str('31')+str(k+1))
plt.subplot(n)
plt.scatter(X_test,y_test,c='k',s=2)
for i,alpha in enumerate([0.1,0.5,0.9]):
sort_order = np.argsort(X_test, axis=0).ravel()
X_test_sorted = np.array(X_test)[sort_order]
#print(np.array(model[alpha]))
predictions_sorted = np.array(model[alpha])[sort_order]
plt.plot(X_test_sorted,predictions_sorted,label=fr"$\tau$={alpha}",lw=0.8)
plt.legend()
plt.title(f'{name[k]}')
plt.tight_layout()
plt.show()
可以看到分位数回归的明显的区间特点。
还有非参数非线性方法的优势,明显XGB和LGBM拟合得更好。
波士顿数据集
上面是人工数据,下面采用真实的数据集进行对比,就用回归最常用的波士顿房价数据集吧:
data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
target = raw_df.values[1::2, 2]
column_names = ['CRIM','ZN','INDUS','CHAS','NOX','RM','AGE','DIS','RAD','TAX','PTRATIO', 'B','LSTAT', 'MEDV']
boston=pd.DataFrame(np.hstack([data,target.reshape(-1,1)]),columns= column_names)取出X和y,划分测试集和训练集
X = boston.iloc[:,:-1]
y = boston.iloc[:,-1]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)拟合预测,对比
alphas = np.arange(0.1, 1, 0.1)
mse_qr, mse_xgb, mse_lgb = [], [], []
r2_qr, r2_xgb, r2_lgb = [], [], []
qr_pred,xgb_pred,lgb_pred={},{},{}
# Train and evaluate
for alpha in alphas:
# Quantile Regression
model_qr = QuantReg(y_train, sm.add_constant(X_train)).fit(q=alpha)
model_pred=model_qr.predict(sm.add_constant(X_test))
mse_qr.append(mean_squared_error(y_test,model_pred ))
r2_qr.append(r2_score(y_test,model_pred))
# XGBoost
model_xgb = xgb.train({"objective": "reg:quantileerror", 'quantile_alpha': alpha},
xgb.QuantileDMatrix(X_train, y_train), num_boost_round=100)
model_pred=model_xgb.predict(xgb.DMatrix(X_test))
mse_xgb.append(mean_squared_error(y_test,model_pred ))
r2_xgb.append(r2_score(y_test,model_pred))
# LightGBM
model_lgb = lgb.train({'objective': 'quantile', 'alpha': alpha,'force_col_wise': True,},
lgb.Dataset(X_train, y_train), num_boost_round=100)
model_pred=model_lgb.predict(X_test)
mse_lgb.append(mean_squared_error(y_test,model_pred))
r2_lgb.append(r2_score(y_test,model_pred))
if alpha in [0.1,0.5,0.9]:
qr_pred[alpha]=model_qr.predict(sm.add_constant(X_test))
xgb_pred[alpha]=model_xgb.predict(xgb.DMatrix(X_test))
lgb_pred[alpha]=model_lgb.predict(X_test)画图查看不同分位点的不同模型的误差和拟合优度:
plt.figure(figsize=(8, 5),dpi=128)
plt.subplot(211)
plt.plot(alphas, mse_qr, label='Quantile Regression')
plt.plot(alphas, mse_xgb, label='XGBoost')
plt.plot(alphas, mse_lgb, label='LightGBM')
plt.legend()
plt.xlabel('Quantile')
plt.ylabel('MSE')
plt.title('MSE across different quantiles')
plt.subplot(212)
plt.plot(alphas, r2_qr, label='Quantile Regression')
plt.plot(alphas, r2_xgb, label='XGBoost')
plt.plot(alphas, r2_lgb, label='LightGBM')
plt.legend()
plt.xlabel('Quantile')
plt.ylabel('$R^2$')
plt.title('$R^2$ across different quantiles')
plt.tight_layout()
plt.show()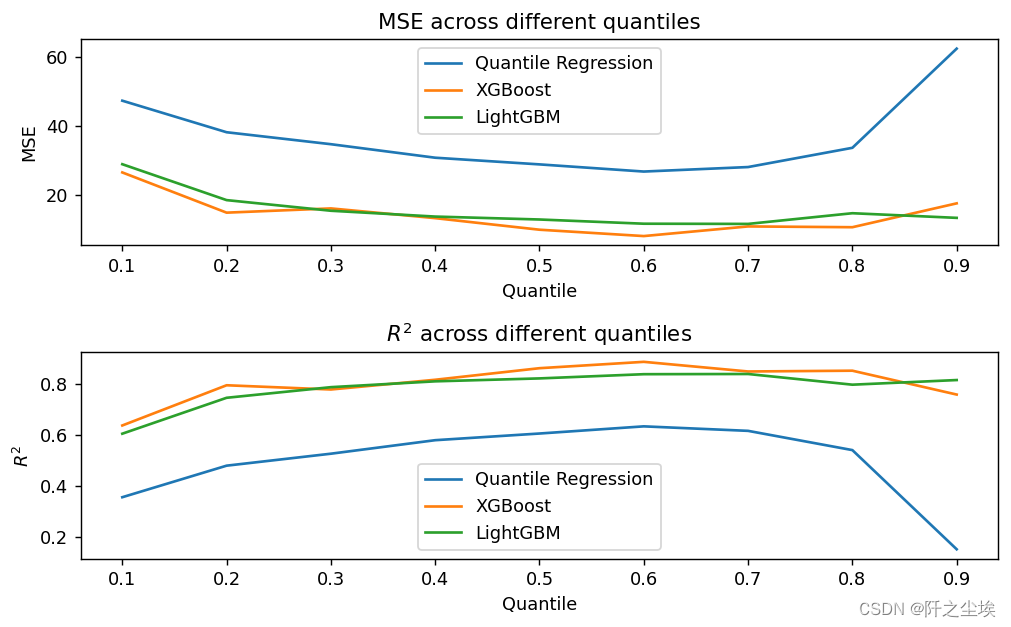
可以看到在分位点为0.6附件三个模型表现效果都比较好,然后模型表现来看,XGB>LGBM>QR,还是两个机器学习模型更厉害。
分位数损失函数和平方和损失函数对比
上面我们得到在分位点为0.6的时候,模型效果表现好,那么分位数模型和普通的MSE损失函数的效果比起来怎么样呢?我们继续对比:
# 定义alpha值
alpha = 0.5
# 分位数回归模型
model_qr = sm.regression.quantile_regression.QuantReg(y_train, sm.add_constant(X_train)).fit(q=alpha)
qr_pred = model_qr.predict(sm.add_constant(X_test))
# XGBoost分位数回归
model_xgb = xgb.train({"objective": "reg:quantileerror", 'quantile_alpha': alpha},
xgb.DMatrix(X_train, label=y_train), num_boost_round=100)
xgb_q_pred = model_xgb.predict(xgb.DMatrix(X_test))
# LightGBM分位数回归
model_lgb = lgb.train({'objective': 'quantile', 'alpha': alpha,'force_col_wise': True},
lgb.Dataset(X_train, label=y_train), num_boost_round=100)
lgb_q_pred = model_lgb.predict(X_test)
# 普通的最小二乘法线性回归
model_lr = LinearRegression()
model_lr.fit(X_train, y_train)
lr_pred = model_lr.predict(X_test)
# 普通的XGBoost
model_xgb_reg = xgb.train({"objective": "reg:squarederror"}, xgb.DMatrix(X_train, label=y_train), num_boost_round=100)
xgb_pred = model_xgb_reg.predict(xgb.DMatrix(X_test))
# 普通的LightGBM
model_lgb_reg = lgb.train({'objective': 'regression', 'force_col_wise': True}, lgb.Dataset(X_train, label=y_train), num_boost_round=100)
lgb_pred = model_lgb_reg.predict(X_test)上面是六个模型,非别是基于分位数回归的XGB,LGBM,线性分位数回归。还有三个基于最普通的MSE损失函数的普通XGB,LGBM和最小二乘线性回归。
# 计算6个模型的MSE和R^2
models = ['QR', 'XGB Quantile', 'LightGBM Quantile', 'Linear Reg', 'XGBoost', 'LightGBM']
preds = [qr_pred, xgb_q_pred, lgb_q_pred, lr_pred, xgb_pred, lgb_pred]
mse_scores = [mean_squared_error(y_test, pred) for pred in preds]
r2_scores = [r2_score(y_test, pred) for pred in preds]画柱状图查看:
colors = sns.color_palette("muted", len(models))
fig, axs = plt.subplots(2, 1, figsize=(9,7))
axs[0].bar(models, mse_scores, color=colors)
axs[0].set_title('MSE Comparison')
axs[0].set_ylabel('MSE')
axs[1].bar(models, r2_scores, color=colors)
axs[1].set_title(r'$R^{2}$ Comparison')
axs[1].set_ylabel(r'$R^{2}$')
plt.tight_layout()
plt.show()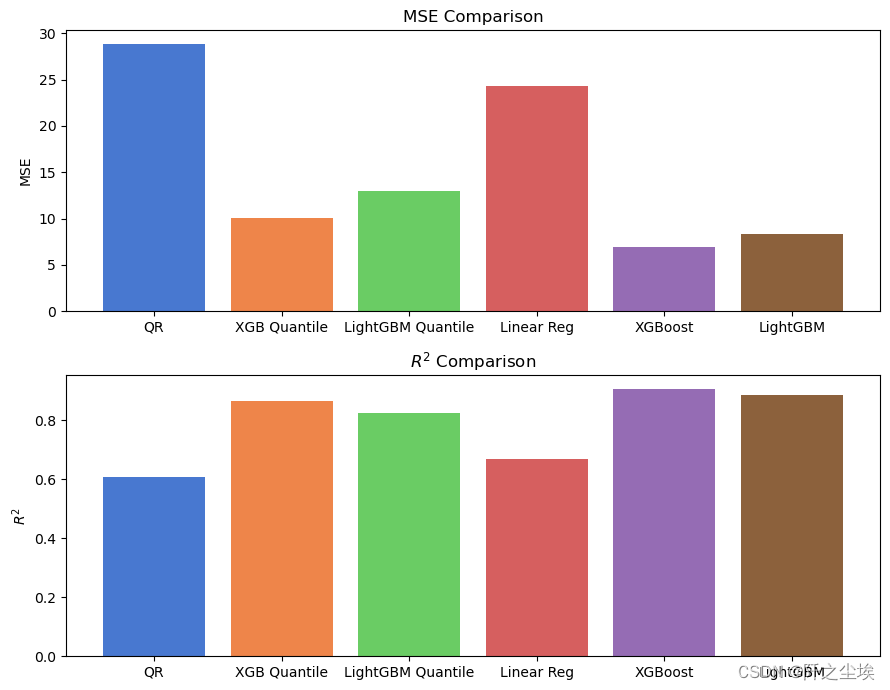
可以看到模型效果来看,XGboost由于Lightgbm优于线性模型。但是分位数回归效果没有MSE损失好,说明在这个数据集表现上,就采用最经典的MSE损失的普通的模型效果会更好。。。
确实是这样的,很多学术创新和改进都不一定比最经典和最常见的方法的效果好。
如果是那种异常值很多的数据,具有异方差的数据 ,可能损失函数改用分位数的会更好。











![VisualStudio[WPF/.NET]基于CommunityToolkit.Mvvm架构开发](https://img-blog.csdnimg.cn/969486e295af482f88c48250d967a8bb.png)