图(graph)的遍历-----广度优先遍历(BFS)

news2025/1/12 15:59:43

目录

前言

广度优先遍历（BFS）

1.基本概念 

2.算法过程 

图的广度优先遍历

1.邻接矩阵

2.邻接表

3.算法比较

前言

        上一期学习了图的深度优先遍历，（深度优先遍历：图(graph)的遍历----深度优先(DFS)遍历-CSDN博客）那这一期我们接着学习图的广度优先遍历（BFS），对于图的广度优先遍历我们也不陌生，在二叉树的层序遍历也就是广度优先遍历的一种了。那对于图的广度优先遍历有有什么不同呢？我们接着往下看。

二叉树的层序遍历（广度优先遍历）

广度优先遍历（BFS）

1.基本概念 

        广度优先搜索（Breadth First Search）简称广搜或者 BFS，是遍历图存储结构的一种算法，既适用于无向图（网），也适用于有向图（网）。

        广度优先遍历是一种图和树的遍历策略，它的核心思想是从一个起始节点开始，访问其所有邻近节点，然后再按照相同的方式访问这些邻近节点的邻近节点。这种遍历方式类似于波纹在水面上扩散的过程。

在广度优先遍历中，我们通常使用一个队列（Queue）来存储待访问的节点。初始时，将起始节点放入队列。然后，执行以下操作直到队列为空：

  1. 从队列中取出一个节点。
  2. 访问该节点，并将其标记为已访问。
  3. 将该节点的所有未被访问的邻近节点加入队列。

2.算法过程 

 下面给大家看一个示例就知道了。

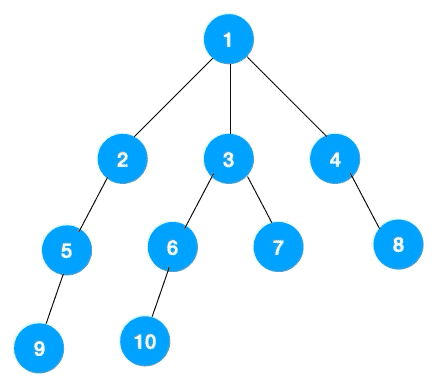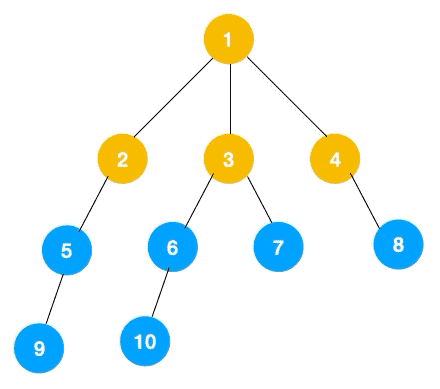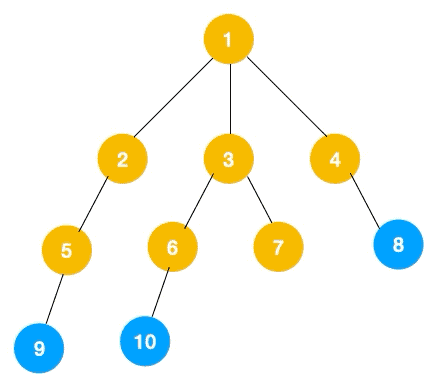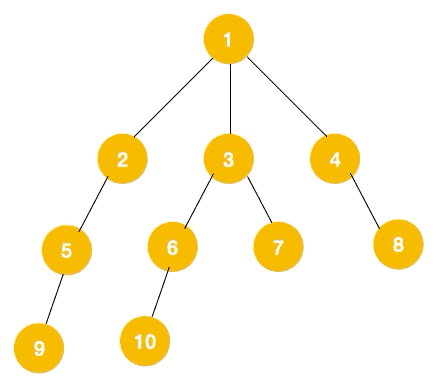
 对于上图这么一个图，从顶点V1出发开始进行广度优先遍历，其过程如下：

开始访问V1，然后V1入队进行访问操作。

接着就是访问与顶点V1连接的顶点V2和V3，依次入队。

 然后就是访问与V3相连的顶点V4,V5依次入队访问。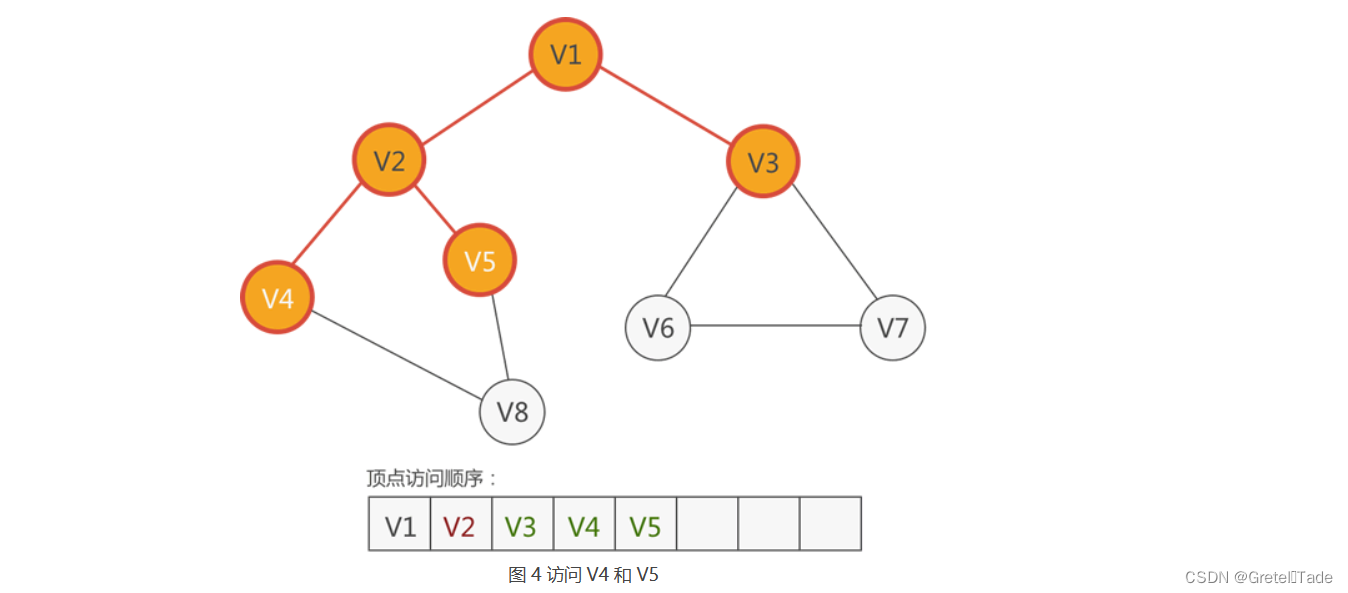

再然后就是与顶点V3相连的顶点V6,V7,执行同样的操作。 

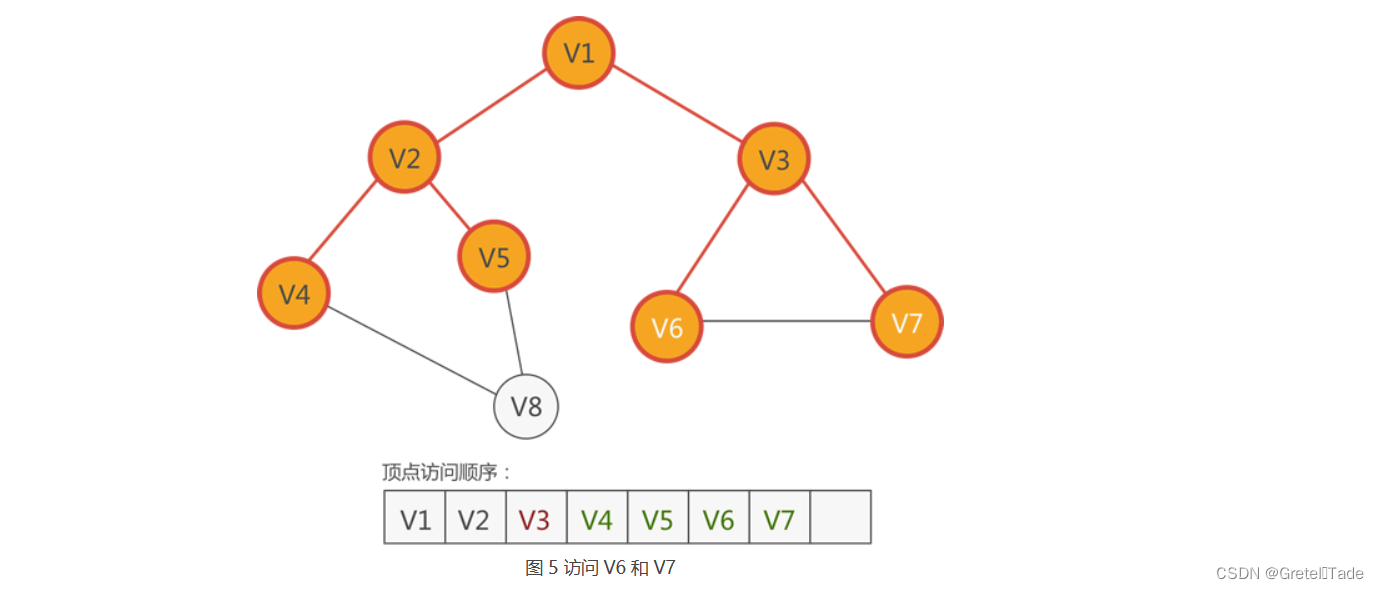 最后就是V8顶点进行访问

 整体结果如下：

看了上面这几个图，我相信大家都理解了广度优先遍历的次序了吧，无非就是一层一层去访问而已。前面我们说过图的两种存储方式，分别是邻接矩阵和邻接表，那下面我们就去学习邻接矩阵和邻接表的广度优先遍历算法，看看同一个图不同的两种存储方式的遍历结果会有那些不同呢？

图的广度优先遍历

广度优先遍历 (Breadth-First-Search,BFS) 要点:

  1. 找到与一个顶点相邻的所有顶点
  2. 标记哪些顶点被访问过，需要一个辅助数组
  3. 需要一个辅助队列

辅助数组visited作用：

是用来标记访问过的节点，初始化全为0，表示都没有访问过，每次访问了一个节点，下标对应的辅助数组的位置设置为1表示已经访问，下次访问之前先去通过visited数组判断这个节点是否访问过，如果访问过就跳过这个节点，反之就进行访问操作。

辅助队列的作用：

用于储存当前访问节点所连接的节点，然后进行入队操作，要去访问的时候就进行出队的操作。

辅助队列代码如下：

头文件(queue.h)代码：

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<string.h>
#include <stdbool.h>

//数据类型
typedef struct datatype { 
	char id[10];
	//……
}
ElemType;

//定义节点
typedef struct node {
	ElemType data;
	struct node* next;
}Node;
//定义队列
typedef struct queue {
	int count;	//计数
	Node* front;//指向队头指针
	Node* rear;//指向队尾指针
}Queue;

void Queue_init(Queue* queue);//初始化
bool isEmpty(Queue* queue);//判空
void enQueue(Queue* queue, ElemType data);//入队
Node* deQueue(Queue* queue);//出队
ElemType head_data(Queue queue);//获取队头数据

queue.c代码： 

#include"queue.h"

//初始化
void Queue_init(Queue* queue) {
	assert(queue);
	queue->front = NULL;
	queue->rear = NULL;
	queue->count=0;
}

//创建节点
Node* create_node(ElemType data) {
	Node* new_node = (Node*)malloc(sizeof(Node));
	if (new_node) {
		new_node->data = data;
		new_node->next = NULL;
		return new_node;
	}
	else
	{
		printf("ERRPR\n");
	}
}

//判断是否空队列
bool isEmpty(Queue* queue) {
	assert(queue);
	if (queue->count == 0)
	{
		return true;
	}
	return false;
}


//入队
void enQueue(Queue* queue, ElemType data) {
	assert(queue);
	Node* new_node = create_node(data);
	if (queue->rear == NULL) {
		queue->front = new_node;
		queue->rear = new_node;
		queue->count++;
	}
	else
	{
		queue->rear->next = new_node;
		queue->rear = new_node;
		queue->count++;
	}

}

//出队
Node* deQueue(Queue* queue) {
	assert(queue);
	if (!isEmpty(queue)) {
		Node* deNode = queue->front;
		queue->front = deNode->next;
		queue->count--;
		return deNode;
	}
	printf("error\n");
	return NULL;
}


//获取队头数据
ElemType head_data(Queue queue) {
	return queue.front->data;
}

1.邻接矩阵

广度优先遍历代码如下：

//01--邻接矩阵
#include"queue.h"//导入头文件


#define Maxint 32767
#define Maxnum 100//最大顶点数

ElemType;
//图的邻接数组
typedef struct graph {
	ElemType vexs[Maxnum];//图数据
	int matrix[Maxnum][Maxnum];//二维数组矩阵
	int vexnum;//点数
	int arcnum;//边数
}Graph;

//节点id查找下标
int Locate_vex(Graph G, char* id) {
	for (int i = 0; i < G.vexnum; i++)
		if (strcmp(G.vexs[i].id,id)==0)
			return i;
	return -1;
}
//节点id查找这个数据体节点
ElemType Locate_data(Graph G, char* id) {
	for (int i = 0; i < G.vexnum; i++)
		if (strcmp(G.vexs[i].id, id) == 0)
			return G.vexs[i];
}

//构造邻接矩阵(无向图，对称矩阵)(有向图)赋权图
void Create_graph(Graph* G) {
	printf("请输入顶点个数和边的个数：\n");
	scanf("%d %d", &G->vexnum, &G->arcnum);//输入点数边数
	printf("请输入顶点数据:\n");
	for (int i = 0; i < G->vexnum; i++) {
		scanf("%s", G->vexs[i].id);
	}
	for (int x = 0; x < G->vexnum; x++) {
		for (int y = 0; y < G->vexnum; y++) {
			if (x == y)
				G->matrix[x][y] = 0;//对角线初始化为0
			else
				G->matrix[x][y] = Maxint;//其他初始化为Maxint
		}
	}
	printf("请输入边相关数据:\n");
	for (int k = 0; k < G->arcnum; k++) {
		char a[10], b[10];
		int w;
		scanf("%s %s %d", a, b, &w);
		//a->b
		int i = Locate_vex(*G, a);
		int j = Locate_vex(*G, b);
		//矩阵赋值
		G->matrix[i][j] = w;
		G->matrix[j][i] = w;//删掉这个，表示有向图
	}
}

//输出矩阵
void print_matrix(Graph G) {
	printf("矩阵为：\n");
	for (int i = 0; i < G.vexnum; i++) {
		for (int j = 0; j < G.vexnum; j++) {
			if (G.matrix[i][j] == Maxint)
				printf("∞\t");
			else
				printf("%d\t", G.matrix[i][j]);
		}
		printf("\n");
	}
	printf("图的顶点个数和边数：%d,%d\n", G.vexnum, G.arcnum);
}

//访问输出
void visit(Graph G,int loca) {
	printf("%s ", G.vexs[loca].id);
}

//广度优先遍历BFS
void BFS(Graph G, char* id) {
	//辅助数组，标记是否访问过
	int* visited = (int*)malloc(sizeof(int) * G.vexnum);
	memset(visited, 0, sizeof(int) * G.vexnum);//初始化为0表示未访问过

	ElemType begin = Locate_data(G, id);//通过输入的id找到这个数据节点
	Queue q;//定义队列
	Queue_init(&q);//初始化队列
	enQueue(&q, begin);//把第一个节点进行入队操作
	visited[Locate_vex(G,id)] = 1;//visited对应的位置标记为1，表示这个节点已经入队，将进行访问操作

	while (!isEmpty(&q)) {//进入到循环
		int location = Locate_vex(G, head_data(q).id);//找到队头节点在图中的位置(下标)
		//把当前队头节点相连的节点依次入队操作
		for (int i = 0; i < G.vexnum; i++) {
			if (G.matrix[location][i] != 0 && !visited[i]) {
				enQueue(&q, G.vexs[i]);
				visited[i] = 1;//入队后标记为1,
			}
		}
		Node*v = deQueue(&q);//进行出队操作
		location = Locate_vex(G, v->data.id);
		visit(G, location);//访问
	}
}

main函数，测试代码：

int main() {
	Graph G;
	Create_graph(&G);
	print_matrix(G);

	printf("\nBFS:\n");
	BFS(G, "B");
}

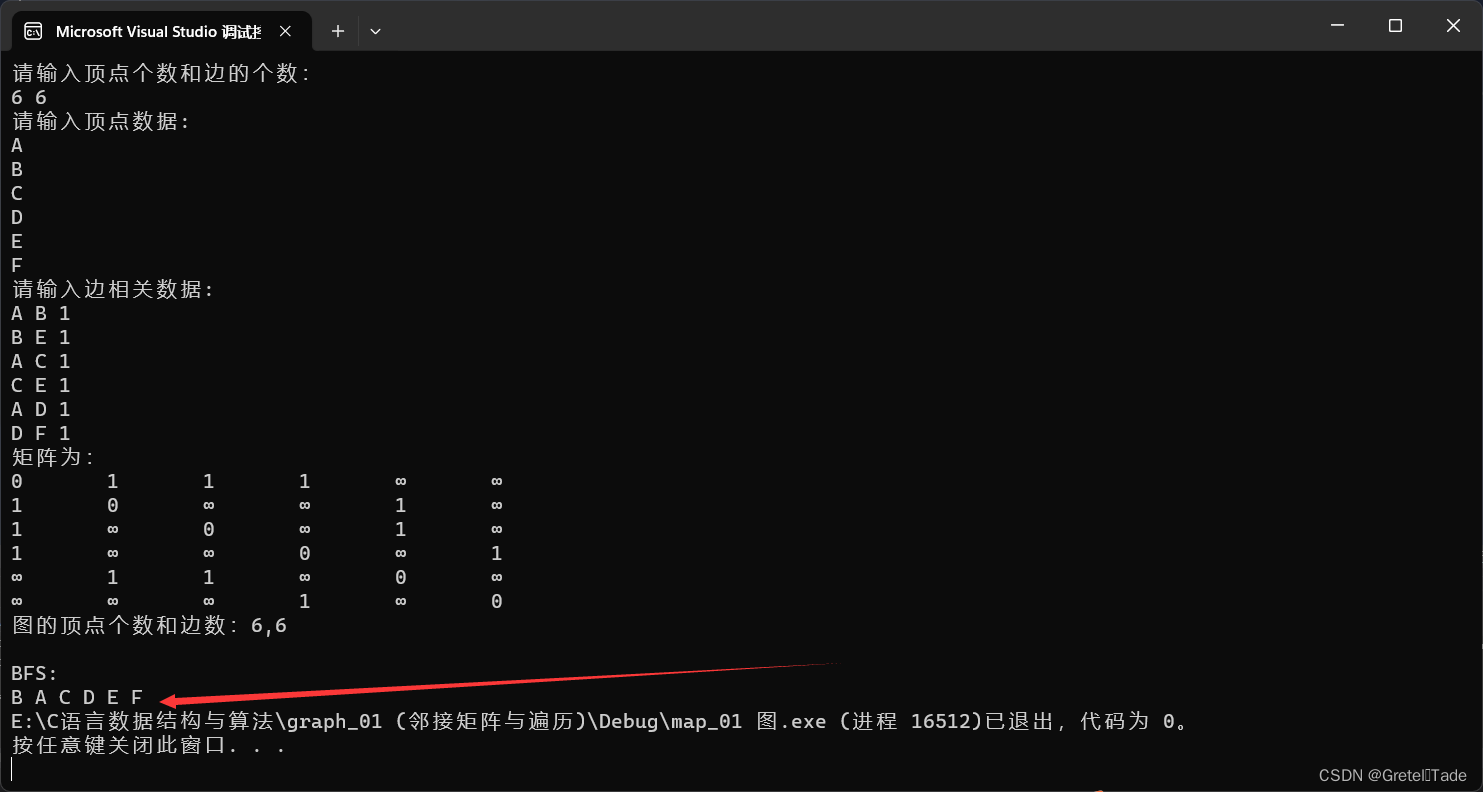
输入的图结构如图所示： 

 

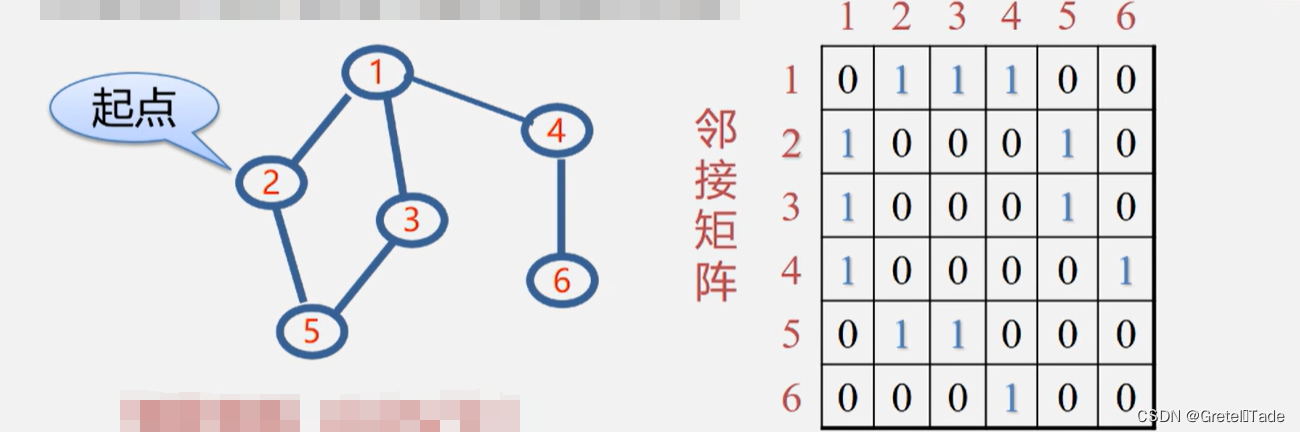
2.邻接表

代码如下：

//02--邻接表
#include"queue.h"

//边节点存储结构
typedef struct arcnode {
	int index;//指向顶点的位置
	int weight;//权
	struct arcnode* nextarc;//指向下一个边节点
}Anode;
//顶点结点存储结构
typedef struct vexnode {
	ElemType data;
	Anode* firstarc;
}Vhead;
//图结构
typedef struct {
	Vhead* vertices;
	int vexnum;
	int arcnum;
}Graph;

//顶点id查找下标
int Locate_vex(Graph G, char* id) {
	for (int i = 0; i < G.vexnum; i++)
		if (strcmp(G.vertices[i].data.id,id)==0)
			return i;
	return -1;
}

//顶点编号查找整个数据
ElemType Locate_data(Graph G, char* id) {
	int index;
	for (int i = 0; i < G.vexnum; i++) {
		if (strcmp(G.vertices[i].data.id, id) == 0) {
			index = i;
			break;
		}
	}
	return G.vertices[index].data;
}

//创建头节点
void Create_vexhead(Graph *G,int n) {
	G->vertices = (Vhead*)malloc(sizeof(Vhead) *n);
	if (!G->vertices) {
		printf("ERROR\n");
		exit(-1);
	}
	else {
		for (int i = 0; i < n ; i++) {
			scanf("%s", G->vertices[i].data.id);
			G->vertices[i].firstarc = NULL;
		}
	}
}
//创建一个边节点
Anode* Create_arcnode(int loca, int w) {
	Anode* arc = (Anode*)malloc(sizeof(Anode));
	if (!arc)
	{
		printf("ERROR\n");
		exit(-1);
	}
	arc->index = loca;
	arc->nextarc = NULL;
	arc->weight = w;
	return arc;
}
//创建邻接表(无向图)（有向图）
void Create_graph(Graph* G) {
	printf("输入顶点数和边数:\n");
	scanf("%d %d", &G->vexnum, &G->arcnum);

	printf("输入顶点数据:\n");
	Create_vexhead(G, G->vexnum);

	printf("输入边数据：\n");
	for (int k = 0; k <G->arcnum; k++) {
		ElemType a, b;
		int w;
		scanf("%s%s%d", a.id, b.id, &w);
		int i = Locate_vex(*G, a.id);
		int j = Locate_vex(*G, b.id);
		//头插法
		//a->b
		Anode* p = Create_arcnode(j, w);
		p->nextarc = G->vertices[i].firstarc;
		G->vertices[i].firstarc = p;
		//如果创建有向图的话，直接把下面的代码删掉即可
		//b->a
		Anode* q = Create_arcnode(i, w);
		q->nextarc = G->vertices[j].firstarc;
		G->vertices[j].firstarc = q;
	}
}

//访问
void visit(Graph G, int index) {
	printf("%s ", G.vertices[index].data.id);
}

//输出图
void print(Graph G) {
	printf("以下是图的顶点连接关系：\n");
	for (int i = 0; i < G.vexnum; i++) {
		printf("%s:", G.vertices[i].data.id);
		Anode* cur= G.vertices[i].firstarc;
		while (cur) {
			visit(G, cur->index);
			cur = cur->nextarc;
		}
		printf("\n");
	}
	printf("顶点和边数分别是：%d %d\n", G.vexnum, G.arcnum);
}

//广度优先遍历BFS
void BFS(Graph G, char* begin_id) {
	//visited 标记是否访问
	int* visited = (int*)malloc(sizeof(int) * G.vexnum);
	memset(visited, 0, sizeof(int) * G.vexnum);//初始化0
	ElemType begin = Locate_data(G, begin_id);
	//初始化队列
	Queue qu;
	Queue_init(&qu);
	//起点入队
	enQueue(&qu, begin);
	visited[Locate_vex(G, begin_id)] = 1;

	while (!isEmpty(&qu)) {
		int index=Locate_vex(G,head_data(qu).id);//获取当前队头元素的图位置
		Anode* cur = G.vertices[index].firstarc;//获取队头连接的顶点位置
		while (cur) {
			if (visited[cur->index] == 0) {
				//如果是未访问过的话，就进行入队操作
				enQueue(&qu, G.vertices[cur->index].data);
				visited[cur->index] = 1;
			}
			cur = cur->nextarc;
		}
		//出队列，遍历
		Node* p = deQueue(&qu);
		visit(G, Locate_vex(G, p->data.id));
	}
}

int main() {
	Graph G;
	Create_graph(&G);
	print(G);

	printf("广度优先遍历结果:\n");
	BFS(G, "A");
	
}

测试结果：

3.算法比较

时间复杂度

邻接矩阵

如果使用邻接矩阵，则BFS对于每一个被访问到的顶点，都要循吓检测矩阵中的整整一行（ n个元素)，总的时间代价为O(n^2)。

邻接表

用邻接表来表示图，虽然有2e个表结点，但只需扫描e个结点即可完成遍历，加上访问n个头结点的时间，时间复杂度为O(n+e)。

空间复杂度

空间复杂度相同，都是O(n)(借用了堆栈或队列)  。

以上就是本期的全部内容了，我们下次见咯！ 

分享一张壁纸： 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1127901.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

玄铁C906——物理内存保护（PMP）介绍

玄铁C906——物理内存保护（PMP）介绍

1、前言 &#xff08;1&#xff09;本文描述的是玄铁C906的物理内存保护机制的实现中&#xff0c;与RISC-V架构手册中完整PMP机制的差异部分&#xff1b; &#xff08;2&#xff09;RISC-V架构的PMP机制&#xff0c;参考博客&#xff1a;《RISC-V架构——物理内存属性和物理内存…
阅读更多...
C算法：输入一个数n，输出1到n之间所有的质数

C算法：输入一个数n，输出1到n之间所有的质数

需求&#xff1a; 写一个函数&#xff0c;输入一个数n&#xff0c;输出1到n之间所有的质数。&#xff08;注&#xff1a;质数又称素数。一个大于1的自然数&#xff0c;除了1和它自身外&#xff0c;不能被其他自然数整除的数叫做质数。&#xff09; 输入样例&#xff1a; 10 …
阅读更多...
Pytorch--3.使用CNN和LSTM对数据进行预测

Pytorch--3.使用CNN和LSTM对数据进行预测

这个系列前面的文章我们学会了使用全连接层来做简单的回归任务&#xff0c;但是在现实情况里&#xff0c;我们不仅需要做回归&#xff0c;可能还需要做预测工作。同时&#xff0c;我们的数据可能在时空上有着联系&#xff0c;但是简单的全连接层并不能满足我们的需求&#xff0…
阅读更多...
《数字图像处理-OpenCV/Python》连载（26）绘制椭圆和椭圆弧

《数字图像处理-OpenCV/Python》连载（26）绘制椭圆和椭圆弧

《数字图像处理-OpenCV/Python》连载&#xff08;26&#xff09;绘制椭圆和椭圆弧 本书京东优惠购书链接&#xff1a;https://item.jd.com/14098452.html 本书CSDN独家连载专栏&#xff1a;https://blog.csdn.net/youcans/category_12418787.html 第 4 章 绘图与鼠标交互 本章…
阅读更多...
在keil中debug分析单片机数据和函数调用过程（c51为例），使用寄存器组导致错误原因分析

在keil中debug分析单片机数据和函数调用过程（c51为例），使用寄存器组导致错误原因分析

寄存器参考 参考2 [寄存器组使用using参考]&#xff08;https://blog.csdn.net/weixin_46720928/article/details/110221835&#xff09; keil中的using关键字参考 官方文档里关于using的说明可参阅2个地方&#xff0c;&#xff08;1&#xff09;keil软件菜单栏->Help->…
阅读更多...
被邀请为期刊审稿时，如何做一个合格的审稿人？官方版本教程来喽

被邀请为期刊审稿时，如何做一个合格的审稿人？官方版本教程来喽

审稿是学术研究中非常重要的环节&#xff0c;它可以确保研究的科学性和严谨性。审稿人的任务是检查文章是否符合学术规范&#xff0c;是否具有创新性&#xff0c;是否具有科学价值&#xff0c;以及是否符合期刊的定位和风格。因此&#xff0c;审稿人需要具有扎实的学术背景和丰…
阅读更多...
SHELL编程基础2

SHELL编程基础2

文章目录 if语句if单分支应用案例 if多分支案例 for循环while循环正则表达式基本正则Perl兼容的正则 if语句 if单分支 if单分支的语法组成&#xff1a; 方式一: if 条件测试;then 命令序列 fi方式二 if 条件测试then 命令序列 fi应用案例 [rootsom day01]# vim user_v2.…
阅读更多...
WPF中的绑定知识详解（含案例源码分享）

WPF中的绑定知识详解（含案例源码分享）

✅作者简介&#xff1a;2022年博客新星 第八。热爱国学的Java后端开发者&#xff0c;修心和技术同步精进。 &#x1f34e;个人主页&#xff1a;Java Fans的博客 &#x1f34a;个人信条&#xff1a;不迁怒&#xff0c;不贰过。小知识&#xff0c;大智慧。 &#x1f49e;当前专栏…
阅读更多...
带你深入了解git

带你深入了解git

目录 1、Git介绍1.1git是什么工具1.2git起到的作用1.2.1 个人开发&#xff1a;1.2.2 多人开发&#xff1a; 2、Git安装与下载项目代码2.1 下载安装git2.2 从仓库下载代码 3、创建仓库及提交代码3.1 创建仓库3.2 将本地代码以及文件提交到远程仓库3.2.1git全局配置3.2.2 远程仓库…
阅读更多...
领域驱动设计：基于DDD的微服务设计实例

领域驱动设计：基于DDD的微服务设计实例

文章目录 项目基本信息战略设计战术设计后续的工作 用一个项目来了解 DDD 的战略设计和战术设计&#xff0c;走一遍从领域建模到微服务设计的全过程&#xff0c;一起掌握 DDD 的主要设计流程和关键 点。 项目基本信息 项目的目标是实现在线请假和考勤管理。功能描述如下&…
阅读更多...
【数据中台建设系列之二】数据中台-数据采集

【数据中台建设系列之二】数据中台-数据采集

​ 【数据中台建设系列之二】数据中台-数据采集 上篇文章介绍了数据中台的元数据管理&#xff0c;相信大家对元数据模块的设计和开发有了一定的了解&#xff0c;本编文章将介绍数据中台另一个重要的模块—数据采集。 一、什么是数据采集 数据采集简单来说就是从各种数据源中抓…
阅读更多...
美颜滤镜SDK，企业技术解决方案

美颜滤镜SDK，企业技术解决方案

企业越来越注重提升用户体验&#xff0c;而美颜滤镜SDK正是满足这一需求的强大工具。美摄美颜滤镜SDK是一款专为企业级应用打造的高效、稳定的美颜滤镜解决方案&#xff0c;能够帮助您的企业在瞬息万变的市场中保持竞争力。 一、强大的美颜滤镜功能 美摄美颜滤镜SDK拥有丰富的…
阅读更多...
【wvp】wvp设备上可以开启tcp被动模式

【wvp】wvp设备上可以开启tcp被动模式

目录 开启了 tcp被动模式 开启UDP模式 地平线不支持这种tcp情况 开启了 tcp被动模式 我的理解是zlm就会是tcp被动收流模式 tcpdump -i any host 10.1.3.7 and tcp 而wvp->浏览器&#xff0c;是SRTP,其实还是基于zlm8000的udp端口出来的 开启UDP模式 tcpdump -i any host…
阅读更多...
面试算法40：矩阵中的最大矩形

面试算法40：矩阵中的最大矩形

题目 请在一个由0、1组成的矩阵中找出最大的只包含1的矩形并输出它的面积。例如&#xff0c;在图6.6的矩阵中&#xff0c;最大的只包含1的矩阵如阴影部分所示&#xff0c;它的面积是6。 分析 直方图是由排列在同一基线上的相邻柱子组成的图形。由于题目要求矩形中只包含数字…
阅读更多...
解析一个月销售额过千万的商业模式——七人拼团

解析一个月销售额过千万的商业模式——七人拼团

在当今的商业环境中&#xff0c;营销策略的运用对于企业的成功至关重要。其中&#xff0c;拼团模式作为一种以社交为核心的营销方式&#xff0c;正逐渐受到越来越多企业的关注。本文将探讨七人拼团模式&#xff0c;分析其奖励机制和特点&#xff0c;为企业家提供新的营销思路。…
阅读更多...
如何设计出优秀的虚拟展厅，设计虚拟展厅有哪些步骤

如何设计出优秀的虚拟展厅，设计虚拟展厅有哪些步骤

引言&#xff1a; 虚拟展厅已经成为了当今数字时代的重要组成部分&#xff0c;无论是展示产品、推广服务&#xff0c;还是展示艺术品和文化遗产&#xff0c;虚拟展厅为用户提供了一个全新的互动体验。如何设计虚拟展厅成了很多人关注的焦点。 一.虚拟展厅设计的基本原则 虚拟…
阅读更多...
5G RedCap工业智能网关

5G RedCap工业智能网关

5G RedCap工业智能网关是当前工业智能化发展领域的重要技术之一。随着物联网和工业互联网的迅速发展&#xff0c;企业对于实时数据传输和高速通信需求越来越迫切。在这种背景下&#xff0c;5G RedCap工业智能网关以其卓越的性能和功能&#xff0c;成为众多企业的首选。 5G RedC…
阅读更多...
双11电视盒子什么牌子好？数码达人测评25款整理电视盒子排名

双11电视盒子什么牌子好？数码达人测评25款整理电视盒子排名

双11买电视盒子什么牌子好&#xff1f;为了推荐更客观&#xff0c;这段时间我进行了25款主流电视盒子的深度测评&#xff0c;从芯片、内存、网络、散热、系统、广告、流畅度等多方面进行对比&#xff0c;整理了电视盒子排名&#xff0c;双十一想买电视盒子不知道怎么选可以参考…
阅读更多...
应用程序无法正常启动0xc000007b的解决策略，多种解决方法分享

应用程序无法正常启动0xc000007b的解决策略，多种解决方法分享

当我们在使用特定的软件或游戏时&#xff0c;我们可能会遇到一个特别令人头疼的问题—那就是"应用程序无法正常启动0xc000007b"的错误。但是&#xff0c;为何会出现这类情况和如何解决呢&#xff1f;接下来的内容&#xff0c;将会详细地为你阐释。 一.0xc000007b错误…
阅读更多...
【小程序】实现一个定制的音乐播放器

【小程序】实现一个定制的音乐播放器

应用地址&#xff1a;https://spacexcode.com/player 介绍 这是为自己制作的一个在线 Web 版的音乐播放器。众所周知&#xff0c;现在市面上的所有的音乐平台都是会员制。而免费的资源却分散在网络上的各个角落&#xff0c;为此&#xff0c;我收集了自己 喜欢的音乐&#xff0…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023