文章目录
先看下目录，看下整体结构
程序 = 数据结构 + 算法。一般在学习到数据结构时都会出现另一个东西，它叫算法。在我看来二者还是有侧重点的，至于为什么学习数据结构时都要带点算法，我的答案是让大家更好的去理解，学习数据结构。因此这个专栏的定位还是主数据结构，辅以算法。
数据结构
什么是数据结构
我见过很多老师在教学时常常把数据结构比作容器。容器非常好理解就是装东西的呗，既然是装东西的，那么大家可以思考这样一个问题，String str = new String(“abc”);这行代码中str好像也存了一个字符串abc，那么它算不算数据结构？如果你没有答案，来看看数据结构的定义：
数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。
答案显而易见，str不是数据结构，它只符合定义中的存储。
数据结构相关单位
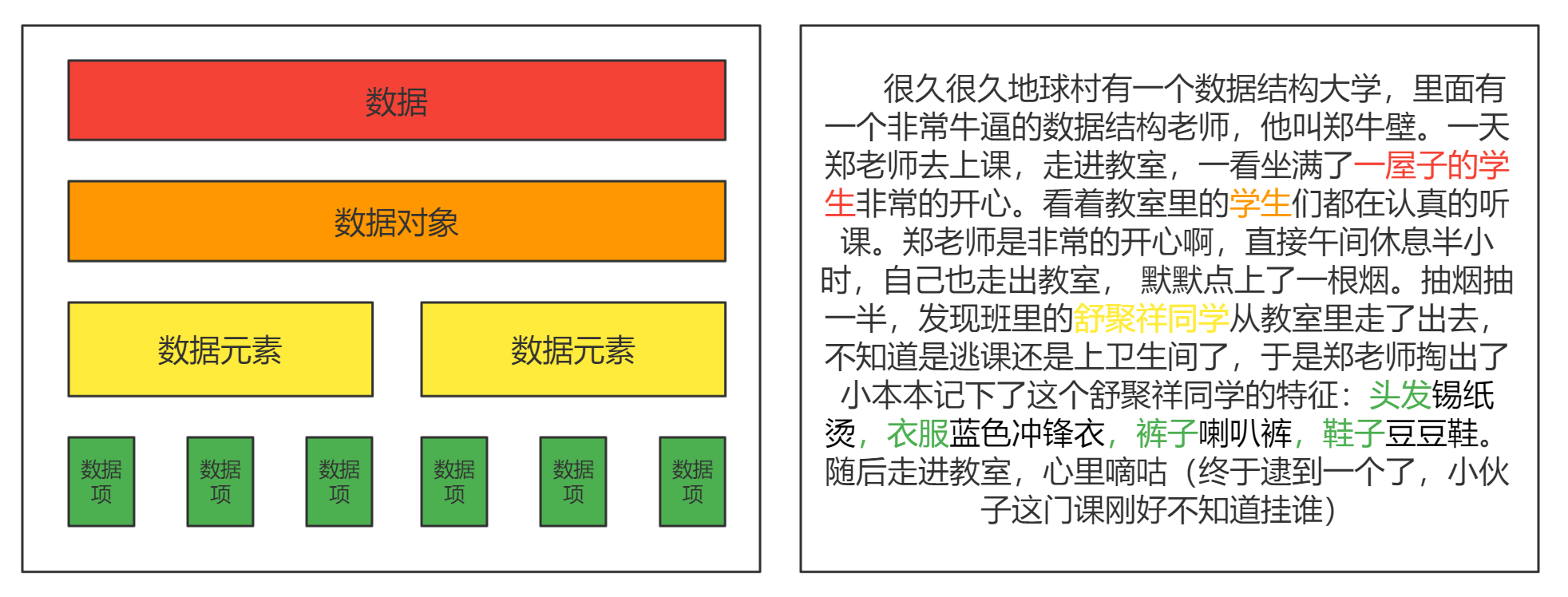
先阅读下图右侧的一个小故事，读完后可以将带颜色的字体与图左侧相关的概念联系起来，看看自己是否有种似曾相识的感觉。
实际开发中我们一般都要定义一个类，并给这个类定义一些属性，就像这样：
// 省去get，set方法等
public class Student{
private String name;
private Integer age;
private String sex;
}
结合上述图片及代码是对图左侧概念的进一步解释：
- 数据：这个概念在数据结构中是最大的单位，一般它指的是数据的集合。对应图里就是一屋子的学生，代码可以是List
- 数据对象：大家理解为Java中的类型即可，诸如一些定义为数据的子集我并不觉得好理解。对应上图就是学生，也就是List里指定的类型Student
- 数据元素：这就是具体的东西了，可以理解为Java中的对象。那么对应上图就是舒聚祥同学
- 数据项：描述数据元素的一些属性。例如图中的头发，衣服，裤子，鞋子。警察叔叔找人一般都怎么问的大家都懂吧
物理结构与逻辑结构
物理结构
- 顺序结构：线性结构指元素的存储位置是连续的
- 链式结构：链式结构指元素的存储位置是不连续的
逻辑结构
数据结构的定义中提到了元素之间存在一种或多种数据关系，这里数据库的基本知识给了我很大启发，所以我总结了自己的记忆方式分享出来。既然是元素之间的关系，我们可以先把所有的关系枚举出来：无关系；一对一；一对多；多对多。根据四个枚举值可以帮助我们记忆以下四个逻辑结构
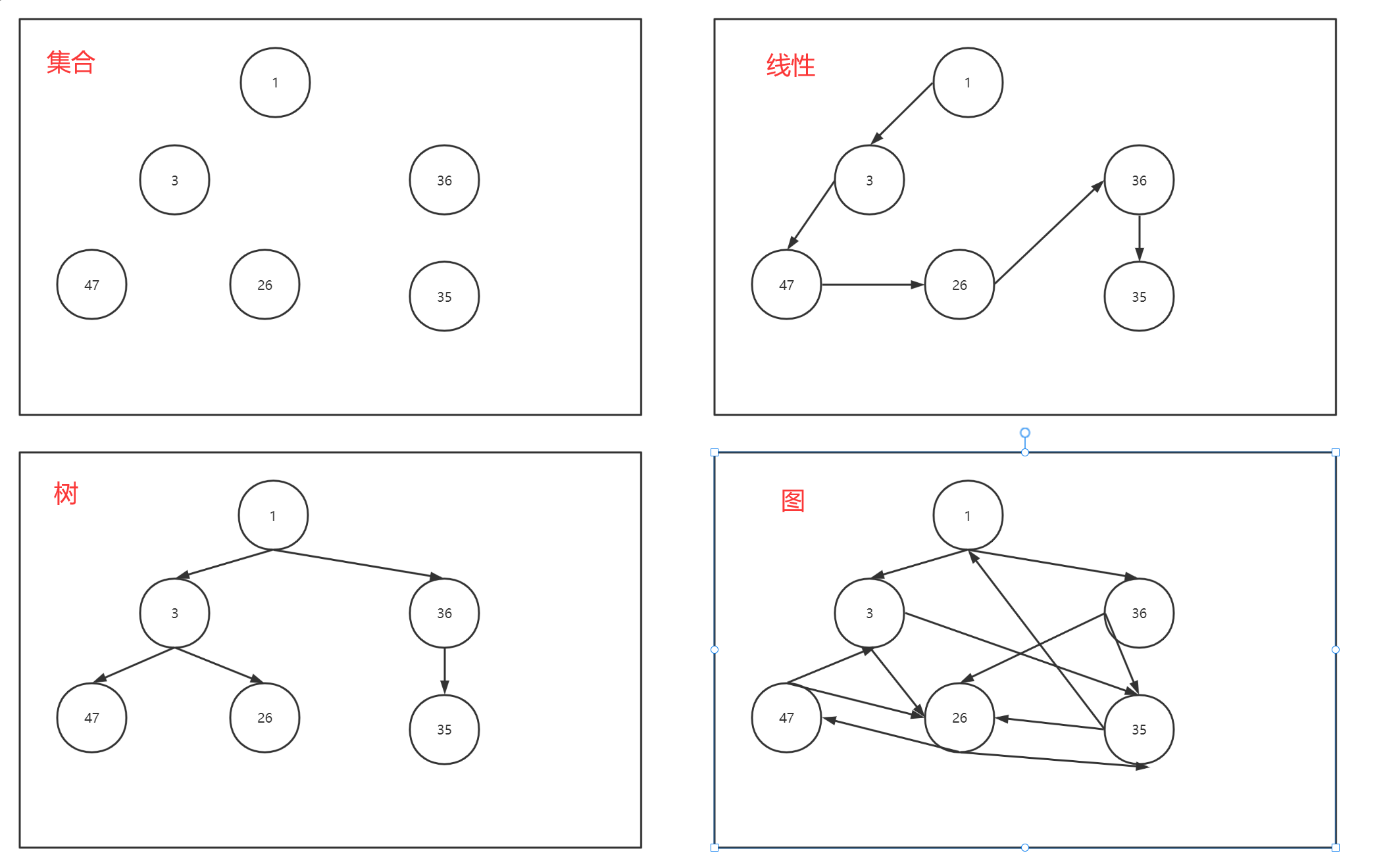
- 集合结构：数据元素之间无关系
- 线性结构：数据元素之间存在一对一的关系
- 树结构：数据元素之间存在一对多的关系
- 图结构：数据元素之间存在多对多的关系
附一张图，结合记忆方式更持久！不单独配图的原因是放在一起我觉得视觉冲撞会更好点，更容易产生联想，更好的记忆。
算法
我对算法的定义很简单，那就是算法=思路（不知道是否片面，好理解就行）。看似高深的东西，实际是我们解决问题的方式，甚至是crud都能称为算法。下面是比较专业的定义：
算法（Algorithm）是指解题方案的准确而完整的描述，是一系列解决问题的清晰指令，算法代表着用系统的方法描述解决问题的策略机制
一个案例认识算法的重要性
从描述上可以看到算法是解决一系列的问题的，著名的高斯算法再科普一下，小时候高斯的数学老师出了一道题，谁能做出来就可以先回家。题目是1~100的加和，这个问题我们用代码来实现一下：
// 方式一
int result = 0;
for (int i = 1; i <= 100; i++) {
result += i;
}
System.out.println("1~100的和是："+result);
// 方式二
int result = 0;
result = (1 + 100) * (100 / 2);
System.out.println("1~100的和是：" + result);
这里例子我想突出的重点是同一个问题，不同的解决方案的效率是不一样的，假设题目变成求1~n的和，那么哪种解决方式更优，算的更快呢？
时间复杂度与空间复杂度
时间复杂度
事前计算时间复杂度与事后判断时间复杂度
上面的案例我没有给出答案，因为没有具体的数据支撑，比如方式一执行用了多少秒，方式二执行用了多少秒。还有一个因素是案例求的是1100的和，这个具象的问题并不能代表1n的和（定义中说的一系列问题）。在算法中用时间复杂度来衡量一个算法的好坏。有两种方式，分别是事前分析与事后判断：
- 事后判断：所谓事后是记录程序的运行时间，这种方式可以比较准确的得出结论。但存在一个致命的问题，如果它很慢，是否需要重写一个？重写的还是慢，又应当如何？
- 事前判断：事前也就是在程序执行之前进行分析，得出一个理论的值来评估算法的好坏，凡事预则立不预则废用在这再合适不过了。一般判断依据有以下几个：
- 硬件（你的程序在哪里跑的）
- 软件（编译后的代码质量）
- 算法自身的结构，逻辑
- 问题的具体数据量（案例中的n到底是多少？）
硬件软件视具体情况而定，暂时抛开算法逻辑本身，我们依据算法的**数据量（输入量）**分析，就能得到一个不错的理论值，它就是事前计算要做的事
函数的渐进式变化
这部分的内容想要通过图片让大家来进一步理解时间复杂度。
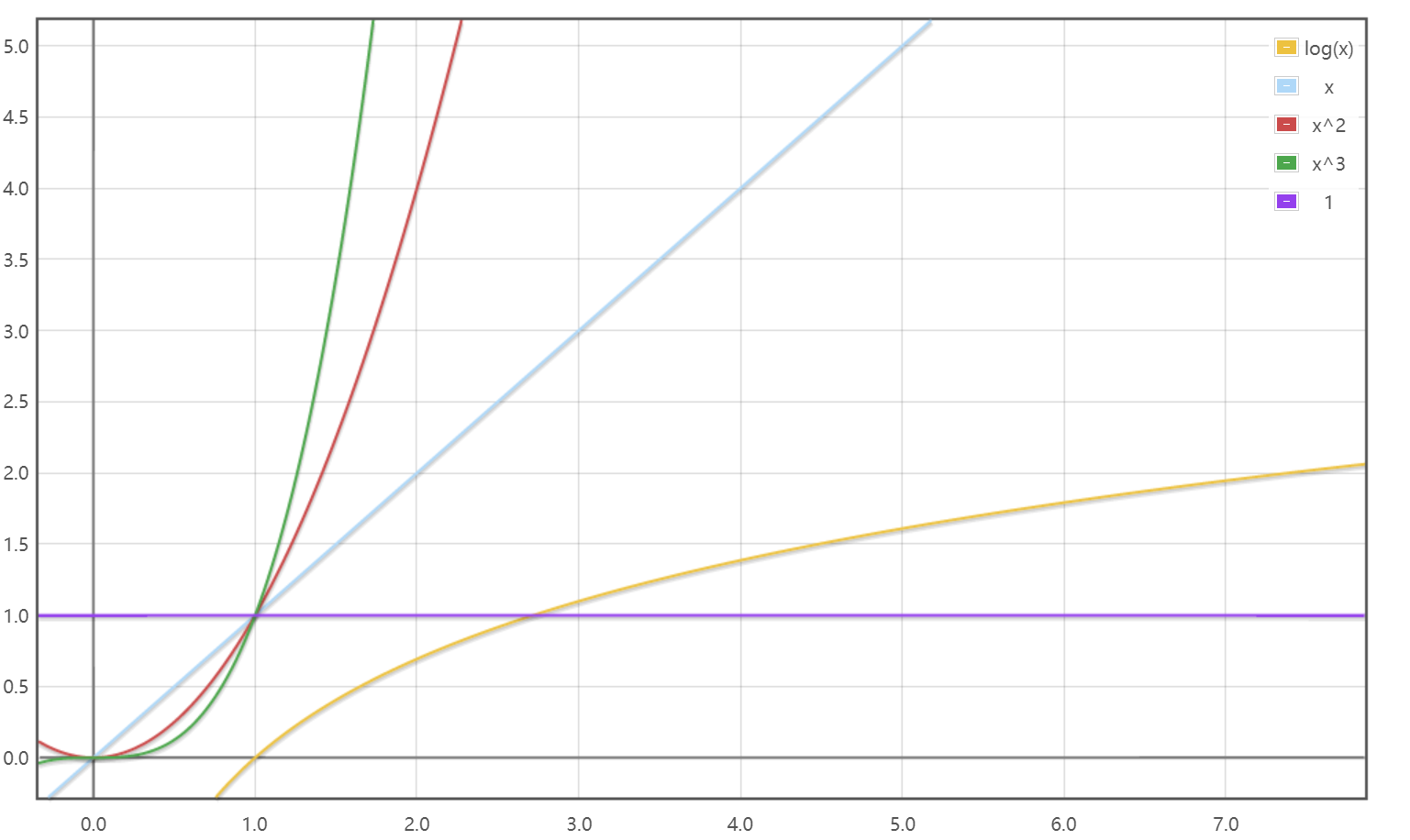
图中共有5个函数的曲线，分别是logx，x，x2,x3,1（常数函数），假设x无限大，那么对应的函数值也会非常的大。上一小节中我们说的输入量跟这里的x是差不多的，这样我们能得出这样一个时间复杂度排序：x3>x2>x>logx>常数函数
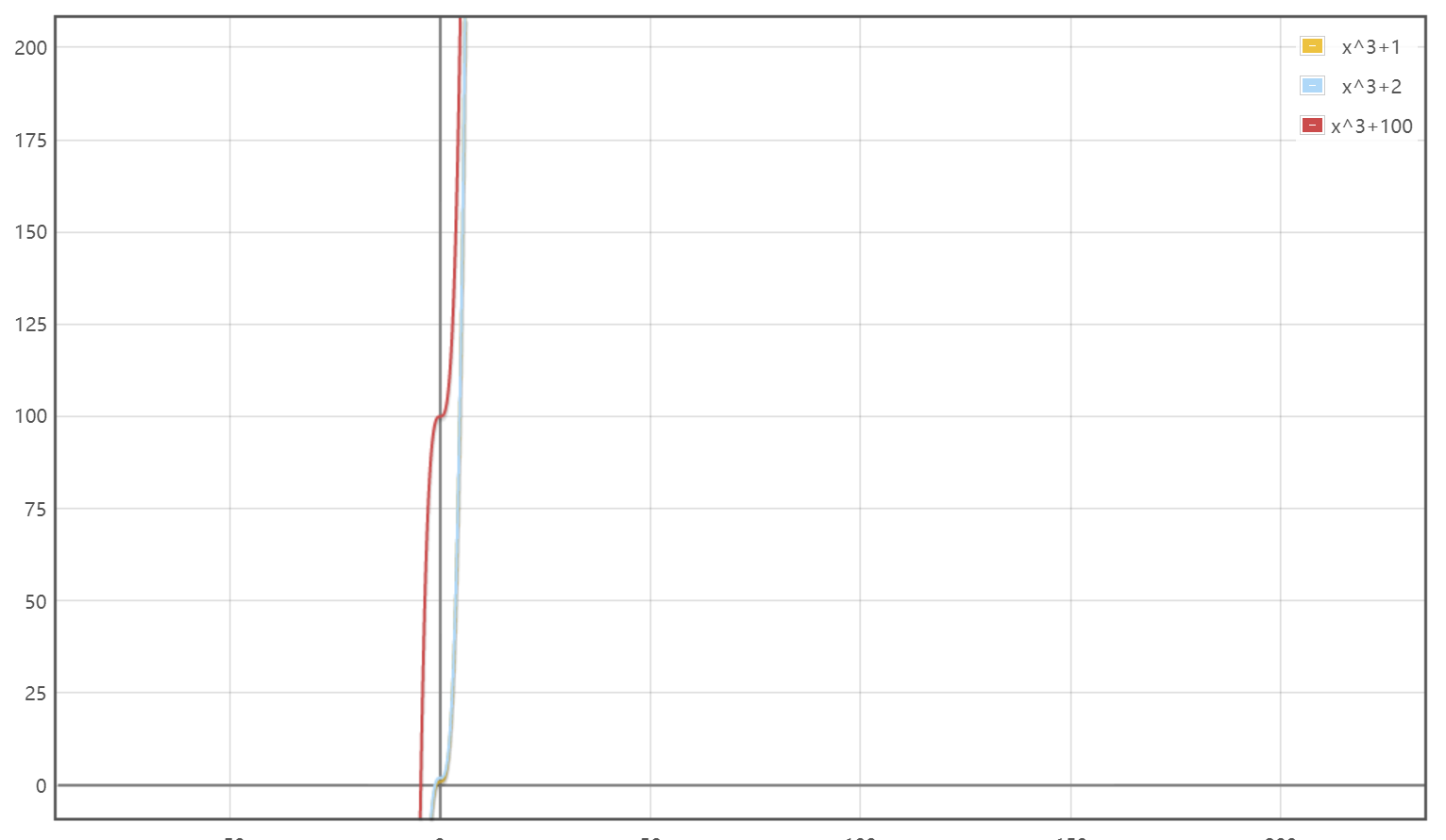
从这个图上可以直观的看出了，当x无限大时，三个函数的函数值是相近的，从图像上来看函数后半段甚至达到了重重合的情况，所以说计算时间复杂度时，常数项是我们可以忽略的
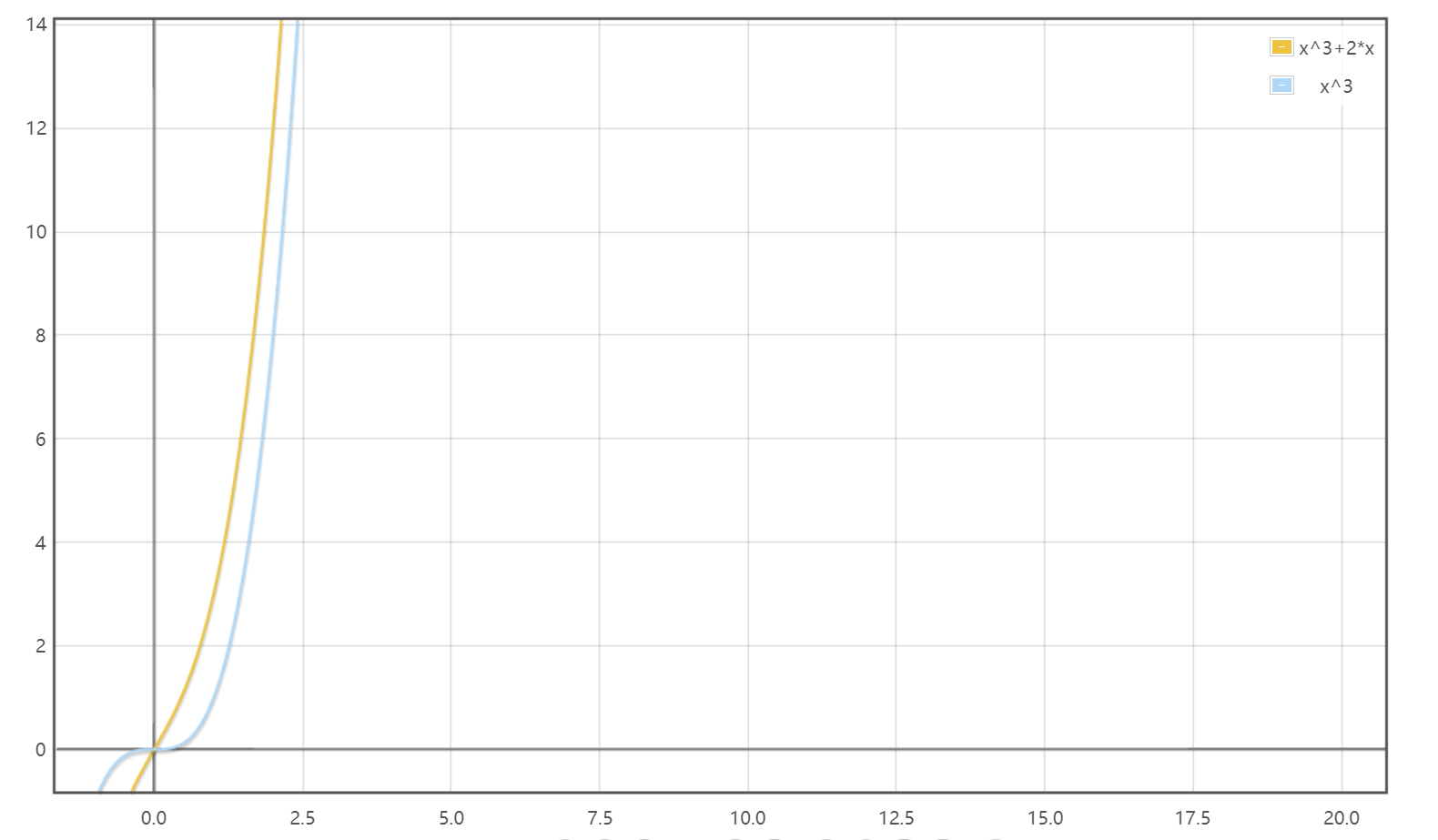
从这个图中可以看出，只要x足够大，那么两个函数的函数值是差不多的。所以说我们不仅仅可以忽略常数，还可以忽略最高项以外的表达式，比如这里的2x
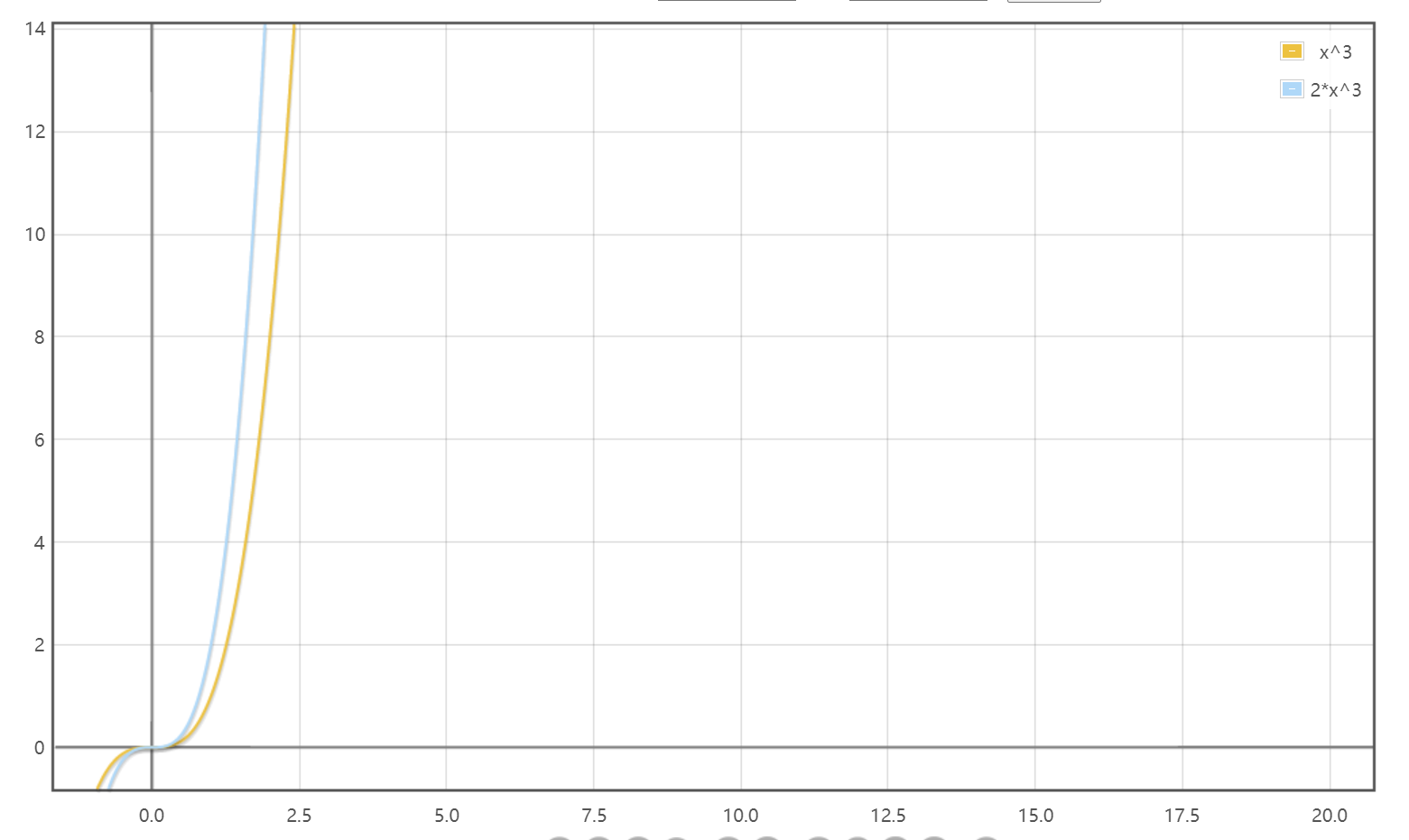两个函数最高次数项的系数不同，随着x的增大，函数值相差也会变大（开口越来越宽），相比于前面两种情况这里的差距会多一些。但是我们也是可以忽略的。
常见函数的时间复杂度
时间复杂度中小到大排序如下（可以从在线网站通过图像直观看出）：
O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n3)<O(2n)<O(n!)<O(nn)
最坏时间与平均时间
通常我们所说的时间复杂度默认指的是最坏的情况，比如求1~n的和，那么最坏的情况就是算法执行了n次。平均时间就是指程序的平均执行时间。
空间复杂度
官方定义：空间复杂度通过计算算法所需的存储空间实现，算法空间复杂度的计算公式记作：S(n) = O(f(n)),其中n是问题的规模，f(n)为语句关于n所占的存储空间函数
