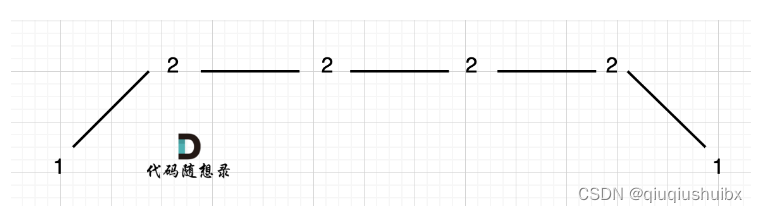前言:贪心无套路
本质:
局部最优去推导全局最优
两个极端
贪心算法的难度一般要么特别简单,要么特别困难,所以我们只能多见识多做题,记住无需数学证明,因为两道贪心基本上毫无关系,我们只需要去思考局部最优即可
贪心的小例子
比如有一堆钞票,你可以拿走十张,如果想达到最大的金额,你要怎么拿?
那肯定是每次拿最大的就行,局部最优就是每次拿最大数额的钞票,全局最优就是最后数额的总和是最大的.
贪心无套路!!!
这里贪心没有任何的模板总结,因为解决不同问题的贪心策略是完全不同的,我们不需要严格的数学证明,如果面对一道题你有这么一种贪心的策略,同时你找不到任何明显的反例,那么就可以照着这个思路来思考问题...
LeetCode T455 分发饼干
题目链接:455. 分发饼干 - 力扣(LeetCode)
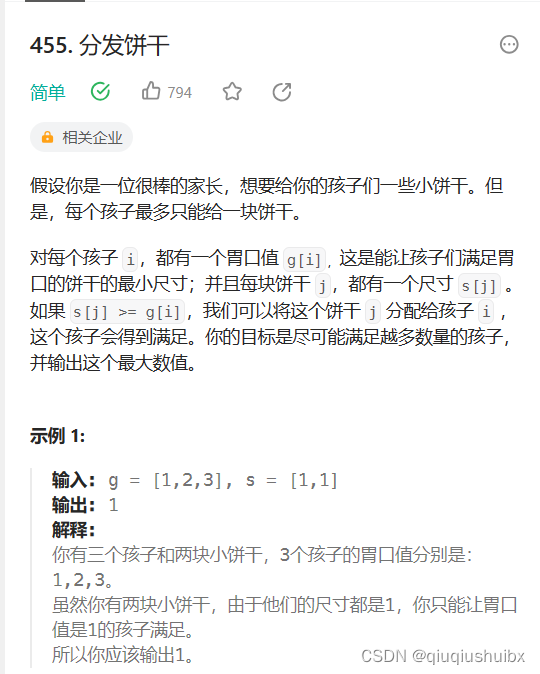

题目思路:
这题我们有两种思路可以解决问题
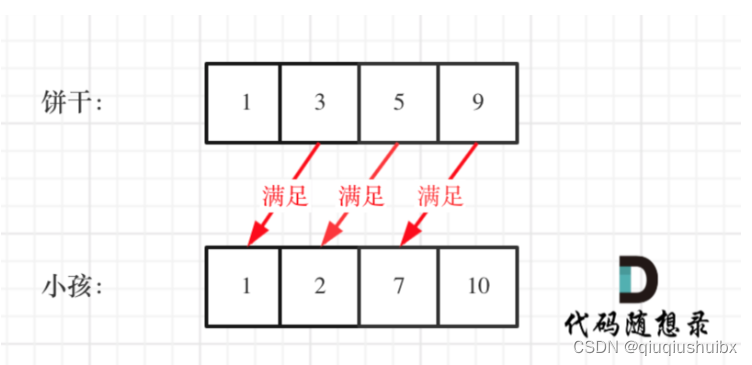
1.优先考虑胃口:大饼干喂饱大胃口
这里的局部最优就是充分利用大饼干来喂饱小孩,全局最优就是喂饱尽可能多的小孩
(尽可能让吃饱的人多)
2.优先考虑饼干:小饼干先喂饱小胃口
这里的局部最优是花费掉最小的饼干,让小饼干物尽其用,全局最优是使饼干的花费更有性价比.
(尽可能让饼干发挥最大的效果)
题目代码
//解法一:
class Solution {
int count = 0;
int start = 0;
public int findContentChildren(int[] g, int[] s) {
Arrays.sort(g);
Arrays.sort(s);
for(int i = 0;i<s.length && start<g.length;i++)
{
if(s[i]>=g[start])
{
start++;
count++;
}
}
return count;
}
}
//解法2
class Solution {
int count = 0;
int start ;
public int findContentChildren(int[] g, int[] s) {
start = s.length-1;
Arrays.sort(g);
Arrays.sort(s);
for(int i = g.length-1;i>=0;i--)
{
if(start >= 0 && s[start]>=g[i])
{
start--;
count++;
}
}
return count;
}
}LeetCode T376 摆动序列
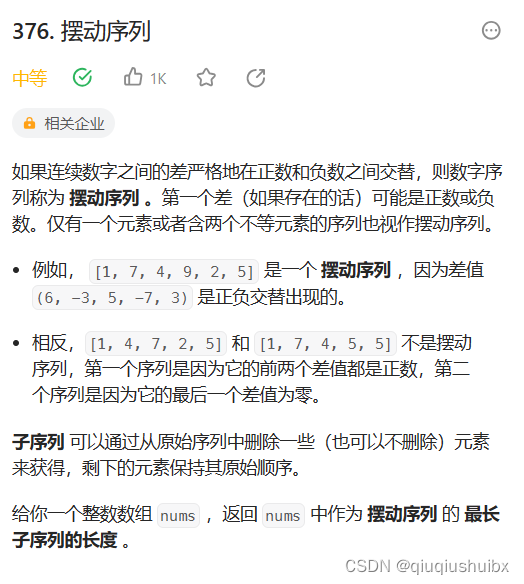

题目链接:376. 摆动序列 - 力扣(LeetCode)
前言
这题我们看到可以删除数组中的元素也可以不删除可能就吓到了,其实是这道题可以用动态规划或者贪心的策略去解决问题,这里我们还是用贪心的解法去解决问题,具体动态规划的思路可以参照网站:代码随想录 (programmercarl.com)
摆动数列的定义
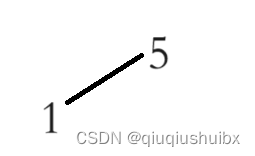
做这题之前我们得明白什么是摆动序列,举个例子[2,6,1,9,3]这个数组,呈现一个波动变化的形态,就称为摆动序列
如果序列只有两个元素,这里就认为摆动序列的长度为2,默认有两个摆动
题目思路:
这题我们首先要考虑情况,我列出以下三种情况:
1.首末元素
2.上下有平坡
3.单调有平坡
变量定义
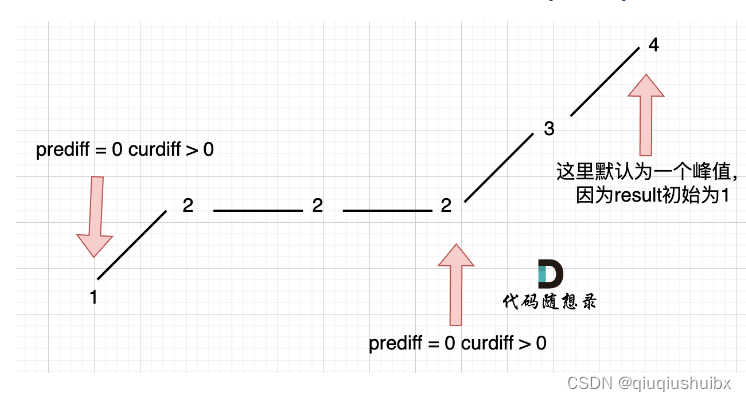
curDiff:记录当前差值 假设目前遍历到的元素为i ,curDiff = nums[i+1] - nums[i]
preDiff:记录之前的差值 preDiff = nums[i] - nums[i-1]
count 记录结果,为了满足默认首尾元素的情况,我们默认count从1开始取值
我们只需要遍历一次数组,满足前后diff不同号即可
注意不能写成curDiff>=0这种情况,因为这样就表示从高或者低值到平坡,是不增加波动的
最后每次结束让pre更新为cur就可以了
这是一个错误的思路,我们是只有遇到了坡度变化才会让pre更新
for(int i = 0;i<nums.length-1;i++) { curDiff = nums[i+1] - nums[i]; if((curDiff>0 && preDiff<=0 ) || (curDiff<0 && preDiff>=0)) { count++; preDiff = curDiff; } }
代码模板:
class Solution {
public int wiggleMaxLength(int[] nums) {
if(nums.length<=1)
{
return nums.length;
}
int preDiff = 0;
int count = 1;
int curDiff = 0;
for(int i = 0;i<nums.length-1;i++)
{
curDiff = nums[i+1] - nums[i];
if((curDiff>0 && preDiff<=0 ) || (curDiff<0 && preDiff>=0))
{
count++;
preDiff = curDiff;
}
}
return count;
}
}LeetCode T53 最大子数组和
题目链接:53. 最大子数组和 - 力扣(LeetCode)

题目思路:
贪心贪的是哪里呢?
如果 -2 1 在一起,计算起点的时候,一定是从 1 开始计算,因为负数只会拉低总和,这就是贪心贪的地方!
局部最优:当前“连续和”为负数的时候立刻放弃,从下一个元素重新计算“连续和”,因为负数加上下一个元素 “连续和”只会越来越小。
全局最优:选取最大“连续和”
局部最优的情况下,并记录最大的“连续和”,可以推出全局最优。
从代码角度上来讲:遍历 nums,从头开始用 count 累积,如果 count 一旦加上 nums[i]变为负数,那么就应该从 nums[i+1]开始从 0 累积 count 了,因为已经变为负数的 count,只会拖累总和。
这相当于是暴力解法中的不断调整最大子序和区间的起始位置。
定义变量:
count:记录局部和
sum:记录目前出现的最大和
思路:一层for循环遍历数组,每次遇到连续子数组之和为负数的时候,就从下一个元素继续开始叠加,每次叠加一个元素对sum进行一次更新.
题目代码:
class Solution {
public int maxSubArray(int[] nums) {
int count = 0;//目前值
int sum = Integer.MIN_VALUE;//目前出现的最大值
for(int i = 0;i<nums.length;i++)
{
count+=nums[i];
sum = Math.max(count,sum);
if(count < 0)
{
count = 0;
}
}
return sum;
}
}