上篇文章中,解释了插入排序、希尔排序、冒泡排序、堆排序及选择排序的原理及具体代码实现本片文章将针对快速排序,快速排序的几种优化方法、快速排序的非递归进行解释。
目录
1. 快速排序原理解析以及代码实现:
2. 如何保证相遇位置的值一定小于所对应的值:
3 优化最坏情况下快速排序的时间复杂度:
4. 对于快速排序代码书写格式的优化(挖坑法):
5. 对于快速排序代码的另一种书写格式优化(前后指针法):
1. 快速排序原理解析以及代码实现:
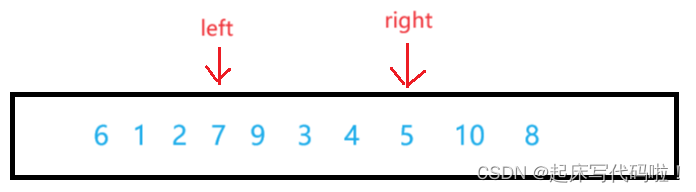
给定下面一个数组:

对于快速排序,其中心思想就是首先选取一个值,一般选择数组中最左边的数据,例如本数组中的。创建一个变量,来保存这个值所对应的下标,为了方便表达,将这个变量命名为
。
在确定了之后,分别从两头遍历数组,定义两个变量用于遍历数组,其中,
,
。
对于遍历数组的过程,需要分成两种情况来查看。其中,用于从左向右遍历数组,
用于从右向左遍历数组。当数组从左向右进行遍历时,一旦遇到比
所对应的值大的数据,则停
在这个数据的所对应的下标处。即:

当数组从右向左进行遍历时,一旦遇到比所对应的值小的数据,则
停在这个数据的所对应的下标处。即:
在找到了符合上面规定的值后,交换两个值在数组中的位置:
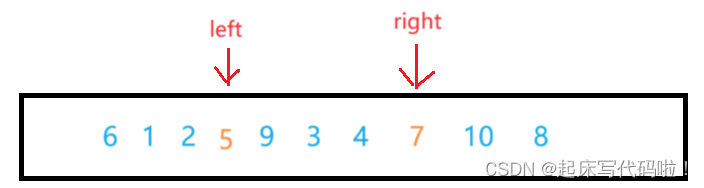
接着继续向下遍历,并且重复之前的动作。当,
相遇时,停止循环,此时的数组可以表示为:

最后,将所对应的值,与此时
或者
所对应的值进行一次交换,便完成了整个流程,用图形表示为:
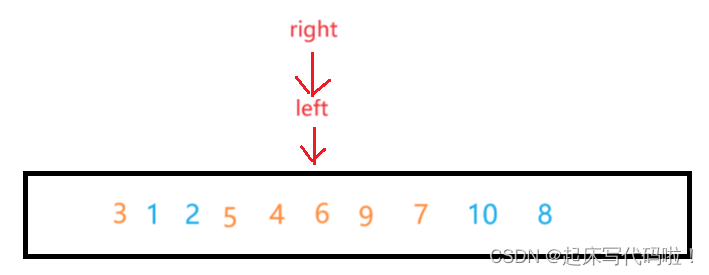
在进行了上面一整套流程后,此时的数组虽然还是无序,但是可以观察到,所对应的值的右半部分的数组的值都大于
所对应的值。
左半部分数组的值都小于
所对应的值。
对于上述流程,可以用下面的代码进行表示:
//部分快排
int PortSort(int* a, int left, int right)
{
int key = left;
while (left < right)
{
//先从右边开始找小的
while( left < right && a[right] >= a[key])
{
right--;
}
//再从左边开始找大的
while(left < right && a[left] <= a[key])
{
left++;
}
//交换找到的值
Swap(&a[left], &a[right]);
}
Swap(&a[key], &a[left]);
return left;
}对于上述给出的代码中,需要注意两个点:
1.在进行遍历数组寻找值的时候,必须先从右边开始遍历找小于所对应的值的数据,再从左边找大于
所对应的值的数据,对于原因将会在文章的后面进行探讨
2.在遍历寻找值的循环中,需要注意循环的两个条件,即
并且
,前面的条件是为了防止下面的两种情况:若从左向右遍历时,不存在比
对应的值大的数据,从右向左遍历时,不存在比
对应的值小的数据。以上两种情况均会导致
的范围超出数组下标的范围,对于第二个条件,如果不加上
,一旦在遍历的过程中,遇到了与
对应的值相等的值,会造成死循环。
完成了上述步骤后,数组依然是无序的,为了处理数组中其他的数据,需要利用到类似二叉树中递归的思想来实现:
对于上述数组,他的数组左半部分的数据都是小于所对应的值的,对于数组的右半部分的数据都是大于
所对应的值的,因此在下面的递归中,需要以
为分界线,
的左半部分为一组,右半部分为一组,对这两组值再次进行一次上面给出代码所对应的操作。
例如,对于左半部分:

此时所对应的值为
,按照上述代码进行操作后,数组可以表示为:
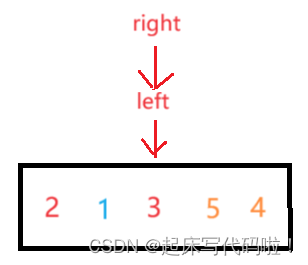
随后,再以为分界线,分出左右部分,对于左右部分进行上述代码的操作,对于左半部分,进行一次操作后,可以表示为:
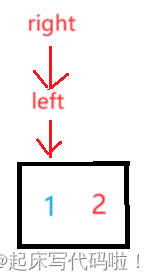
此时,再向下进行递归,的左半区间不存在,
的右半区间只有一个值。因此,对于上面两种情况,视作递归结束的条件。
上面只是展示了每一次的递归中,数组的左半部分的情况,对于右半部分原理相同,这里不再进行赘述。当作伴部分,右半部分的递归都结束后,整个区间会变成有序的区间,即:

对于上述递归,可以用下列代码进行实现:
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
return;
int keyi = PortSort(a, begin, end);
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}测试函数如下:
void TestQuickSort()
{
int e[] = { 6,1,2,7,9,3,4,5,10,8 };
int size = sizeof(e) / sizeof(int);
QuickSort(e, 0,size-1);
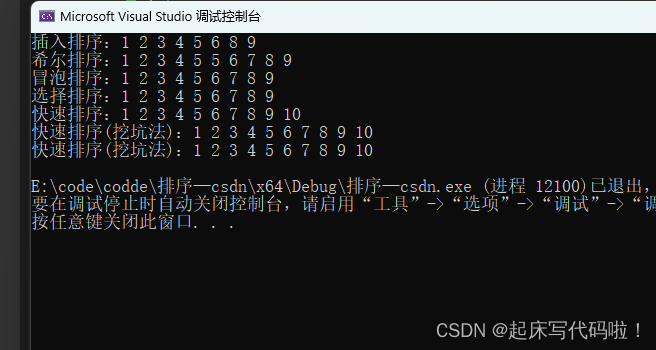
printf("快速排序:");
ArrayPrint(e, size);
}结果如下:
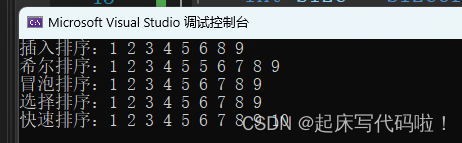
2. 如何保证相遇位置的值一定小于 所对应的值:
所对应的值:
上面说到,在进行遍历寻找值这一步骤时,一定要先从右边开始向左遍历来找到比对应的值小的值,再从左边向右开始遍历,来寻找比
对应值大的值,原因如下:
例如对于上面给出的数组,对于相遇的前一步情况:
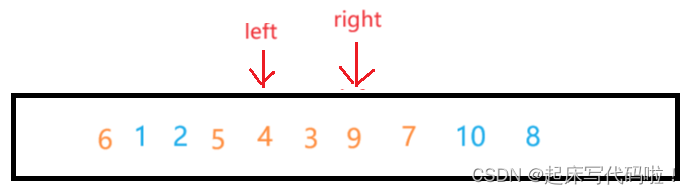
假设左边先进行遍历去寻找值,再从右边向左遍历来寻找值,则二者相遇的位置为:
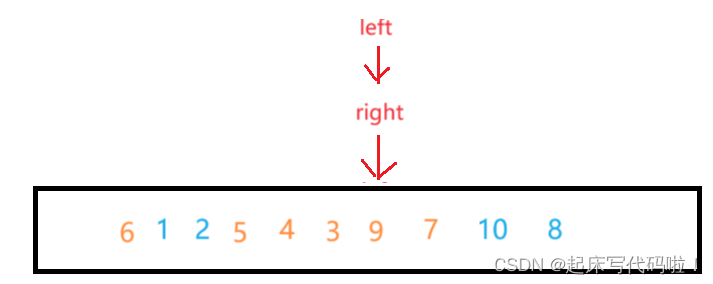
此时,如果按照上面代码的内容对对应的值和
位置对应的值进行交换,则:
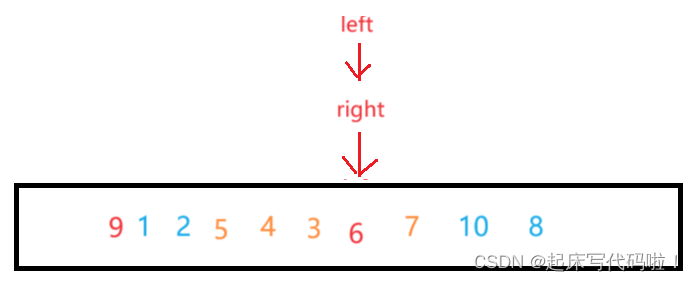
此时,比对应的值大的值不只是只存在右边。
这里需要注意,先从右边往左边遍历的,对应的是的位置在数组的左端。当
在数组的右端时,需要先从左边向右遍历。
3 优化最坏情况下快速排序的时间复杂度:
快速排序的时间复杂度一般都认为是,但是对于下面的一种情况:

前面说到,在快速排序中,当取左端的值时,应该优先从右边开始遍历,对于例子中这种完全升序,或者说大部分区间都是升序的情况,每次从右端进行遍历时,都必须遍历到数组的最左边。因此,对于一个有
个数据的这样的数组来说,从右向左遍历的次数为
次,这种情况下的快速排序的时间复杂度为
。为了优化这种情况,这里引入三数取中的方法。代码如下:因为原理就是简单的两数相比,所以不做过多解释:
//三数取中
int GetMidi(int* a, int left, int right)
{
int mid = (left + right) / 2;
if (a[left] < a[mid])
{
if (a[right] > a[mid])
{
return mid;
}
else if (a[left] > a[right])
{
return left;
}
else
{
return right;
}
}
else//(a[left] > a[mid];
{
if (a[mid] > a[right])
{
return mid;
}
else if (a[left] < a[right])
{
return left;
}
else
{
return right;
}
}
} 在构建了三数取中函数之后,需要对之前的快速排序代码进行修改。修改的部分为:首先在函数的开头创建一个变量
用于接受三数取中函数
的返回值。接着,让
对应的数值与后续
下标对应的数据(即最左端,或者最右端)用交换函数交换即可。
4. 对于快速排序代码书写格式的优化(挖坑法):
对于挖坑法,具体的实现原理如下:
首先还是确认以及
所对应的值,例如在下面的例子中
(注:为了方便演示原理,下面的情况不包括三数取中,但是在书写代码时,使用三数取中的方法与上方的使用发放相同)

首先确定一个,这里按照左端处理,创建一个变量
,令
,接着,确定
所在的下标就是第一个坑位。在确认了第一个坑位后,与上面的快速排序相同,都需要先从右端开始遍历来找到比
小的值,即:

随后,直接让所指向的值覆盖到
的位置,再让
指向的位置变成新的坑,即:

再从左边向右进行遍历,找到比小的值,并且让这个值覆盖到坑位
中,再令下图中的
成为新的坑位:

继续从右向左进行遍历,再从左向右遍历,直到相遇为止,即:
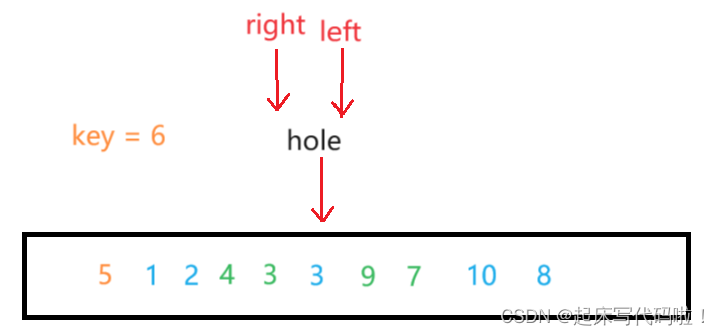
最后,再令二者相遇的位置赋值即可。然后再按照上面的思想递归即可。代码实现为:
//快排优化(挖坑法)
int QuickDigSort(int* a, int begin, int end)
{
int mid = GetMidi(a, begin, end);
Swap(&a[begin], &a[mid]);
int key = a[begin];
int hole = begin;
while (begin < end)
{
//先从右边开始找小的
while (begin < end && a[end] >= key)
{
end--;
}
a[hole] = a[end];
hole = end;
//再从左边开始找大的
while (begin < end && a[begin] <= key)
{
begin++;
}
a[hole] = a[begin];
hole = begin;
}
a[hole] = key;
return hole;
}
void QuickSort2(int* a, int begin, int end)
{
if (begin >= end)
return;
int keyi = QuickDigSort(a, begin, end);
QuickSort2(a, begin, keyi - 1);
QuickSort2(a, keyi + 1, end);
}测试函数如下:
void TestQuickDigSort()
{
int f[] = { 6,1,5,3,9,10,7,4,2,8 };
int size = sizeof(f) / sizeof(int);
QuickSort2(f, 0, size - 1);
printf("快速排序(挖坑法):");
ArrayPrint(f, size);
}运行结果如下:

5. 对于快速排序代码的另一种书写格式优化(前后指针法):
对于前后指针法,就是通过控制两个指针,这里分别命名为,
。通过控制这两个指针的动作时序来完成对于数组的排序,中心思想如下:
对于指针的作用,就是用来寻找比
小的值(
的意义与上面相同),对于指针
的动作时序,分为下面两种情况: 当
没有遇到比
大的值时,
一直紧跟着
,当
遇到比
大的值后,令
的位置处于这个值的前面。
继续令向后遍历,如果又找到了比
小的值,则交换这个值,与
后面的值。
例如对于下面的数组:
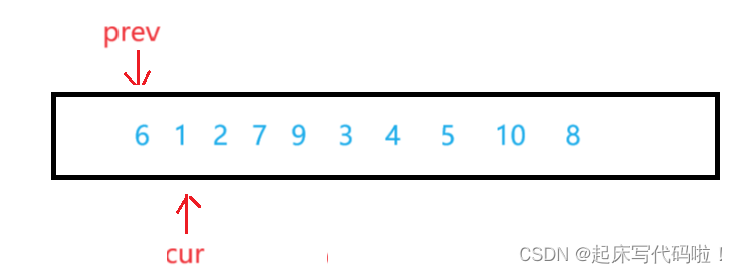
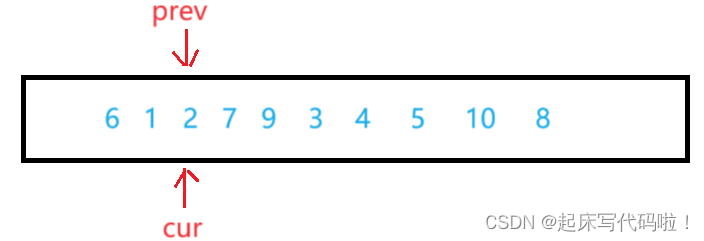
按照上面所说的思想,在没有遇到比
大的值时,
一直紧跟着
运动,即:
此时,再向下运动,遇到了比
大的值,令
继续向后遍历,直至找到比
小的值,令
停在比
大的值的前面,即:

再向下运动后,遇到了比
小的值,令
后面的值与比
小的值交换,即:

接着继续向下遍历,此时指向的位置为:
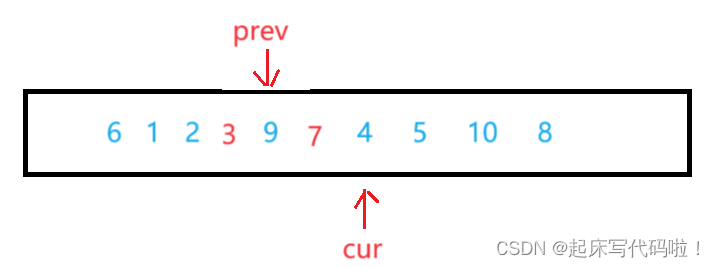
此时再对两个指针指向的值进行交换,即:
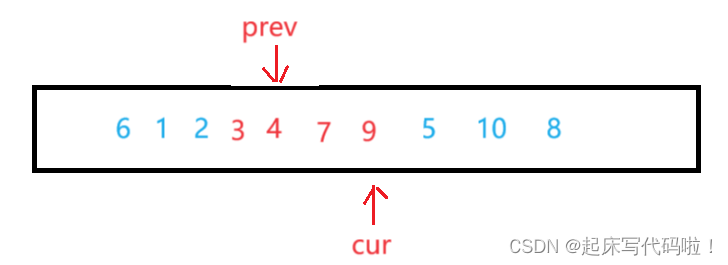
在遍历结束时,数组如下:
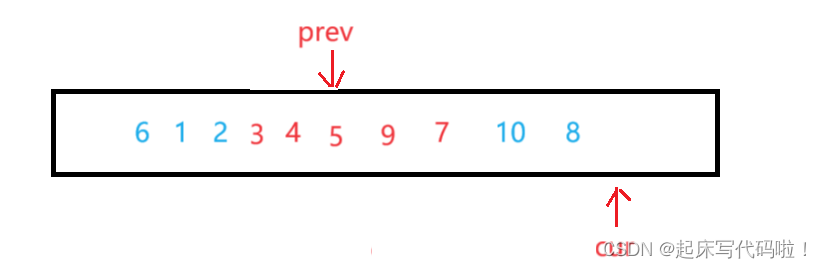
在结束遍历后,交换位置的值与
的值,即:
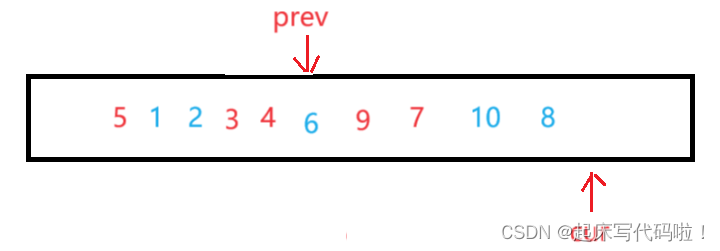
交换完后,比小的值都位于
左边,比
大的值都位于
右边。
总览上面的整个过程,当遇到了比大的值后,两个指针便开始拉开差距。此时
每次向后遍历,都会找到一个比
大的值,并且形成一个比
大的值的区间,在其期间,
一直保持不动,直到
遇到一个
小的值,
在向后指向第一个比
大的值并且交换,此后
每找到一个
小的值,都会把之前
大的值置换到后面,把
小的值置换到前面。
代码如下:
//快速排序(前后指针法)
int QuickTailSort(int* a, int begin, int end)
{
int key = begin;
int prev = begin, cur = begin+1;
while (cur <= end)
{
if (a[cur] < a[key])
{
Swap(&a[++prev], &a[cur]);
}
cur++;;
}
Swap(&a[key], &a[prev]);
return prev;
}测试函数如下:
void TestQuickTailSort()
{
int g[] = { 5,1,6,9,3,10,4,7,2,8 };
int size = sizeof(g) / sizeof(int);
QuickSort3(g, 0, size - 1);
printf("快速排序(挖坑法):");
ArrayPrint(g, size);
}运行结果如下:









![[C++] C++入门](https://img-blog.csdnimg.cn/7e7ee437538b4345b91ec9476932a568.png)