5年前发生的一件事，成为了我职业生涯的重要转折点。当时的我在交大读研，对互联网求职一无所知，但仍然硬着头皮申请了 Microsoft 实习生。面试官让我在白板上写出“快速排序”代码，我畏畏缩缩地写了一个“冒泡排序”，并且还写错了。从面试官的表情上，我知道失败了。

此次失利倒逼我开始刷算法题。我采用“扫雷游戏”式的学习方法，两眼一抹黑刷题，扫到不会的“雷”就通过查资料把它“排掉”，配合周期性总结，幸运地，我在秋招斩获了多家大厂的 Offer 。

当前的就业环境不好，找工作也卷的很，各种面试题也是千奇百怪。回想自己当初在“扫雷式”刷题中被炸的满头包的痛苦，思考良久，我意识到“前期刷题必看”的资料太有必要，可以使让我们在初入职场少走许多弯路。

内容结构

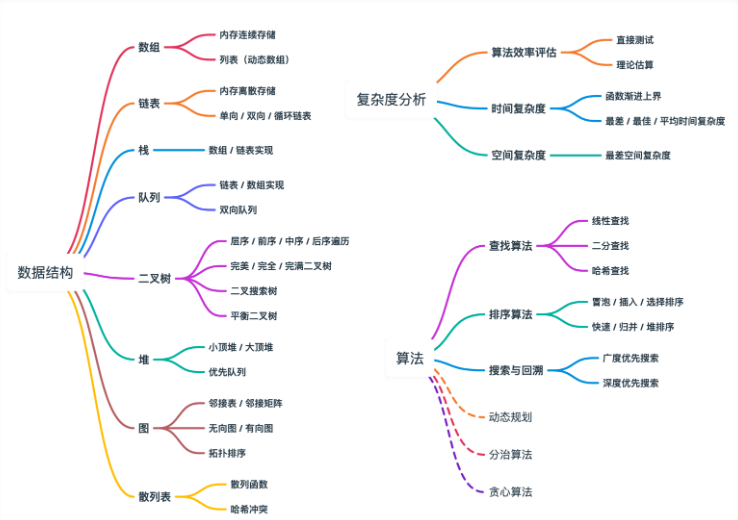
介绍的内容分为复杂度分析、数据结构、算法三个部分，限于篇幅原因，我下面会举2个案例，以 Python 讲解，当然也支持JAVA、C++、GO、C#等编程语言，完整版内容在下方

完整版材料

本文项目源码、数据、技术交流提升，均可加交流群获取，群友已超过2000人，添加时最好的备注方式为：来源+兴趣方向，方便找到志同道合的朋友

方式①、添加微信号：dkl88191，备注：来自CSDN +研究方向
方式②、微信搜索公众号：Python学习与数据挖掘，后台回复：图解算法数据结构

在本文中，重点和难点知识会主要以动画、图解的形式呈现，而文字的作用则是作为动画和图的解释与补充。

环境安装

推荐使用开源轻量的 VSCode 作为本地 IDE ，下载并安装 VSCode，在 VSCode 的插件市场中搜索 python ，安装 Python Extension Pack。

案例1

数组

数组 Array 是一种将 相同类型元素 存储在连续内存空间的数据结构，将元素在数组中的位置称为元素的索引 Index。

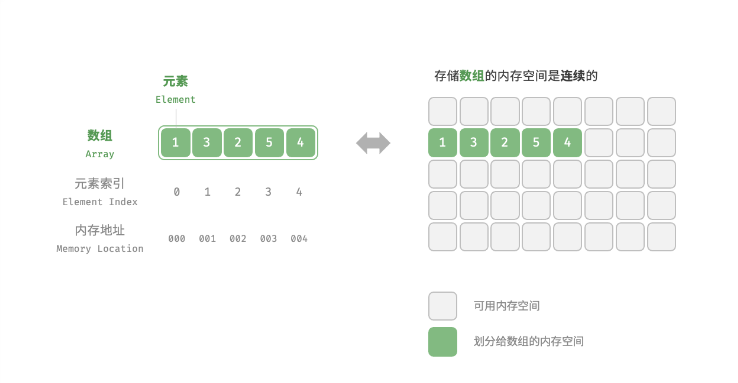
观察上图，我们发现数组首元素的索引为0。你可能会想，这并不符合日常习惯，首个元素的索引为什么不是1呢，这不是更加自然吗？我认同你的想法，但请先记住这个设定，后面讲内存地址计算时，我会尝试解答这个问题。

数组有多种初始化写法。根据实际需要，选代码最短的那一种就好。

""" 初始化数组 """
arr = [0] * 5  # [ 0, 0, 0, 0, 0 ]
nums = [1, 3, 2, 5, 4]  

优点：在数组中访问元素非常高效。这是因为在数组中，计算元素的内存地址非常容易。给定数组首个元素的地址、和一个元素的索引，利用以下公式可以直接计算得到该元素的内存地址，从而直接访问此元素。

为什么数组元素索引从 0 开始编号？ 根据地址计算公式，索引本质上表示的是内存地址偏移量，首个元素的地址偏移量是0 ，那么索引是0 也就很自然了。

访问元素的高效性带来了许多便利。例如，我们可以在 时间内随机获取一个数组中的元素。

""" 随机访问元素 """
def randomAccess(nums):
    # 在区间 [0, len(nums)) 中随机抽取一个数字
    random_index = random.randint(0, len(nums))
    # 获取并返回随机元素
    random_num = nums[random_index]
    return random_num

缺点：数组在初始化后长度不可变。 由于系统无法保证数组之后的内存空间是可用的，因此数组长度无法扩展。而若希望扩容数组，则需新建一个数组，然后把原数组元素依次拷贝到新数组，在数组很大的情况下，这是非常耗时的。

""" 扩展数组长度 """
# 请注意，Python 的 list 是动态数组，可以直接扩展
# 为了方便学习，本函数将 list 看作是长度不可变的数组
def extend(nums, enlarge):
    # 初始化一个扩展长度后的数组
    res = [0] * (len(nums) + enlarge)
    # 将原数组中的所有元素复制到新数组
    for i in range(len(nums)):
        res[i] = nums[i]
    # 返回扩展后的新数组
    return res

数组中插入或删除元素效率低下。假设我们想要在数组中间某位置插入一个元素，由于数组元素在内存中是“紧挨着的”，它们之间没有空间再放任何数据。因此，我们不得不将此索引之后的所有元素都向后移动一位，然后再把元素赋值给该索引。删除元素也是类似，需要把此索引之后的元素都向前移动一位。总体看有以下缺点：

• 时间复杂度高： 数组的插入和删除的平均时间复杂度均为 ，其中 为数组长度。
• 丢失元素： 由于数组的长度不可变，因此在插入元素后，超出数组长度范围的元素会被丢失。
• 内存浪费： 我们一般会初始化一个比较长的数组，只用前面一部分，这样在插入数据时，丢失的末尾元素都是我们不关心的，但这样做同时也会造成内存空间的浪费。

数组常用操作

数组遍历

以下介绍两种常用的遍历方法。

""" 遍历数组 """
def traverse(nums):
    count = 0
    # 通过索引遍历数组
    for i in range(len(nums)):
        count += 1
    # 直接遍历数组
    for num in nums:
        count += 1

数组查找

通过遍历数组，查找数组内的指定元素，并输出对应索引。

""" 在数组中查找指定元素 """
def find(nums, target):
    for i in range(len(nums)):
        if nums[i] == target:
            return i
    return -1

数组典型应用

随机访问:如果我们想要随机抽取一些样本，那么可以用数组存储，并生成一个随机序列，根据索引实现样本的随机抽取。

二分查找:例如前文查字典的例子，我们可以将字典中的所有字按照拼音顺序存储在数组中，然后使用与日常查纸质字典相同的“翻开中间，排除一半”的方式，来实现一个查电子字典的算法。

深度学习:神经网络中大量使用了向量、矩阵、张量之间的线性代数运算，这些数据都是以数组的形式构建的。数组是神经网络编程中最常使用的数据结构。

案例2

快速排序

快速排序 Quick Sort 是一种基于“分治思想”的排序算法，速度很快、应用很广。

快速排序的核心操作为哨兵划分，其目标为：选取数组某个元素为基准数，将所有小于基准数的元素移动至其左边，大于基准数的元素移动至其右边。哨兵划分的实现流程为：

• 以数组最左端元素作为基准数，初始化两个指针 i , j 指向数组两端；
• 设置一个循环，每轮中使用 i / j 分别寻找首个比基准数大 / 小的元素，并交换此两元素；
• 不断循环步骤 2. ，直至 i , j 相遇时跳出，最终把基准数交换至两个子数组的分界线；

哨兵划分执行完毕后，原数组被划分成两个部分，即左子数组和右子数组 ，且满足左子数组任意元素<基准数< 右子数组任意元素。因此，接下来我们只需要排序两个子数组即可。

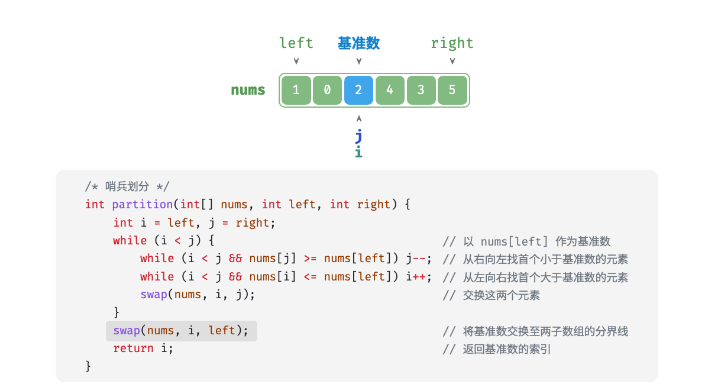
""" 哨兵划分 """
def partition(self, nums, left, right):
    # 以 nums[left] 作为基准数
    i, j = left, right
    while i < j:
        while i < j and nums[j] >= nums[left]:
            j -= 1  # 从右向左找首个小于基准数的元素
        while i < j and nums[i] <= nums[left]:
            i += 1  # 从左向右找首个大于基准数的元素
        # 元素交换
        nums[i], nums[j] = nums[j], nums[i]
    # 将基准数交换至两子数组的分界线
    nums[i], nums[left] = nums[left], nums[i]
    return i  # 返回基准数的索引

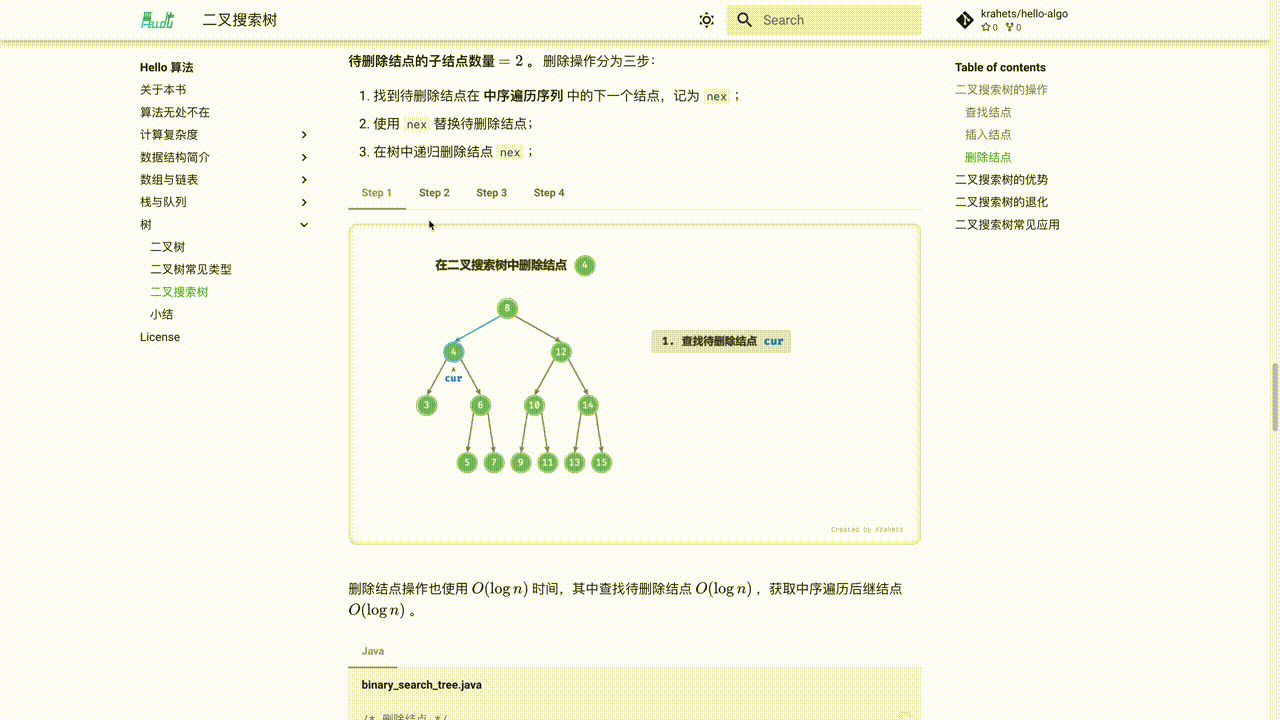
算法流程

• 首先，对数组执行一次「哨兵划分」，得到待排序的 左子数组 和 右子数组 。
• 接下来，对 左子数组 和 右子数组 分别 递归执行「哨兵划分」……
• 直至子数组长度为 1 时 终止递归 ，即可完成对整个数组的排序。

观察发现，快速排序和「二分查找」的原理类似，都是以对数阶的时间复杂度来缩小处理区间。

算法特性

快排为什么快？

基准数优化

普通快速排序在某些输入下的时间效率变差。举个极端例子，假设输入数组是完全倒序的，由于我们选取最左端元素为基准数，那么在哨兵划分完成后，基准数被交换至数组最右端，从而左子数组长度为 n-1 、右子数组长度为0。这样进一步递归下去，每轮哨兵划分后的右子数组长度都为0，分治策略失效，快速排序退化为冒泡排序了。

为了尽量避免这种情况发生，我们可以优化一下基准数的选取策略。首先，在哨兵划分中，我们可以随机选取一个元素作为基准数 。但如果运气很差，每次都选择到比较差的基准数，那么效率依然不好。

进一步地，我们可以在数组中选取3个候选元素（一般为数组的首、尾、中点元素），并将三个候选元素的中位数作为基准数，这样基准数“既不大也不小”的概率就大大提升了。当然，如果数组很长的话，我们也可以选取更多候选元素，来进一步提升算法的稳健性。采取该方法后，时间复杂度劣化最差的概率极低。

""" 选取三个元素的中位数 """
def median_three(self, nums, left, mid, right):
    # 使用了异或操作来简化代码
    # 异或规则为 0 ^ 0 = 1 ^ 1 = 0, 0 ^ 1 = 1 ^ 0 = 1
    if (nums[left] > nums[mid]) ^ (nums[left] > nums[right]):
        return left
    elif (nums[mid] < nums[left]) ^ (nums[mid] > nums[right]):
        return mid
    return right

""" 哨兵划分（三数取中值） """
def partition(self, nums, left, right):
    # 以 nums[left] 作为基准数
    med = self.median_three(nums, left, (left + right) // 2, right)
    # 将中位数交换至数组最左端
    nums[left], nums[med] = nums[med], nums[left]
    # 以 nums[left] 作为基准数
    # 下同省略...

尾递归优化

普通快速排序在某些输入下的空间效率变差。仍然以完全倒序的输入数组为例，由于每轮哨兵划分后右子数组长度为 0 ，那么将形成一个高度为 n-1 的递归树，此时使用的栈帧空间大小劣化至 O(n) 。

为了避免栈帧空间的累积，我们可以在每轮哨兵排序完成后，判断两个子数组的长度大小，仅递归排序较短的子数组。由于较短的子数组长度不会超过 n/2，因此这样做能保证递归深度不超过log(n) ，即最差空间复杂度被优化至O(log(n)) 。

""" 快速排序（尾递归优化） """
def quick_sort(self, nums, left, right):
    # 子数组长度为 1 时终止
    while left < right:
        # 哨兵划分操作
        pivot = self.partition(nums, left, right)
        # 对两个子数组中较短的那个执行快排
        if pivot - left < right - pivot:
            self.quick_sort(nums, left, pivot - 1)  # 递归排序左子数组
            left = pivot + 1     # 剩余待排序区间为 [pivot + 1, right]
        else:
            self.quick_sort(nums, pivot + 1, right)  # 递归排序右子数组
            right = pivot - 1    # 剩余待排序区间为 [left, pivot - 1]