前言

想要精通算法和SQL的成长之路 - 系列导航

一. 找到最终的安全状态

原题链接

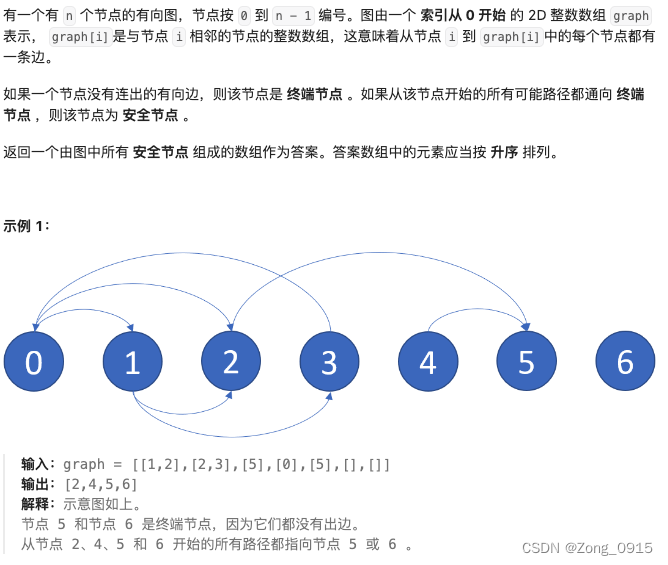
我们从题目中可以看出来：

• 出度为0的，就是终端节点。
• 如果存在路径通向终端节点，那么该节点就是安全节点。那么终端节点本身也可以作为安全节点。
• 而题目要求我们返回的是安全节点。
• 满足题目要求的节点，一定是和终端节点相连的节点。

思路如下：

1. 我们构建有向邻接图，并且统计出度。
2. 出度为0的丢到队列中。
3. 每层循环，处理出度为0的节点（终端节点），我们反向拿到它的前置节点（因此构建邻接图的时候要反向构建有向邻接图）， 更新它的出度。若前置节点的出度为0，说明它之前就是一个安全节点，现在成为了终端节点。
4. 遍历完毕之后，再遍历一遍出度数组，把所有出度为0的节点更新到结果集中即可。

1.1 初始化邻接图

int n = graph.length;
// 初始化邻接图和出度数组
List<Integer>[] adj = new ArrayList[n];
int[] outDegree = new int[n];
for (int i = 0; i < n; i++) {
    adj[i] = new ArrayList<>();
}

1.2 构建反向邻接图

// 构建邻接图和出度数组，这里的索引就是一条有向边的起点。
for (int i = 0; i < n; i++) {
    // 出度的个数，就是二维的长度
    outDegree[i] = graph[i].length;
    // 反向构建邻接图
    for (int j = 0; j < graph[i].length; j++) {
        adj[graph[i][j]].add(i);
    }
}

1.3 BFS遍历

// 将出度为0的入队
LinkedList<Integer> queue = new LinkedList<>();
for (int i = 0; i < n; i++) {
    if (outDegree[i] == 0) {
        queue.offer(i);
    }
}
while (!queue.isEmpty()) {
    int size = queue.size();
    for (int i = 0; i < size; i++) {
        Integer cur = queue.poll();
        // adj[cur] 就是 pre --> 终端节点，拿到的所有 pre
        for (Integer pre : adj[cur]) {
            // 出度 -1，若为0，继续入队
            if (--outDegree[pre] == 0) {
                queue.offer(pre);
            }
        }
    }
}

1.4 完整代码

public class Test802 {
    public List<Integer> eventualSafeNodes(int[][] graph) {
        int n = graph.length;
        // 初始化邻接图和出度数组
        List<Integer>[] adj = new ArrayList[n];
        int[] outDegree = new int[n];
        for (int i = 0; i < n; i++) {
            adj[i] = new ArrayList<>();
        }
        // 构建邻接图和出度数组，这里的索引就是一条有向边的起点。
        for (int i = 0; i < n; i++) {
            // 出度的个数，就是二维的长度
            outDegree[i] = graph[i].length;
            // 反向构建邻接图
            for (int j = 0; j < graph[i].length; j++) {
                adj[graph[i][j]].add(i);
            }
        }
        // 将出度为0的入队
        LinkedList<Integer> queue = new LinkedList<>();
        for (int i = 0; i < n; i++) {
            if (outDegree[i] == 0) {
                queue.offer(i);
            }
        }
        while (!queue.isEmpty()) {
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                Integer cur = queue.poll();
                // adj[cur] 就是 pre --> 终端节点，拿到的所有 pre
                for (Integer pre : adj[cur]) {
                    // 出度 -1，若为0，继续入队
                    if (--outDegree[pre] == 0) {
                        queue.offer(pre);
                    }
                }
            }
        }
        // 最终出度为0的全部加入到结果集中
        ArrayList<Integer> res = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            if (outDegree[i] == 0) {
                res.add(i);
            }
        }
        return res;
    }
}