算法设计

问题描述

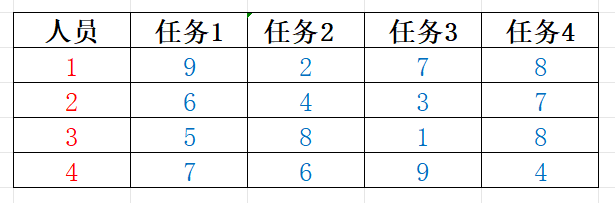
有n（n≥1）个任务需要分配给n个人执行，每个任务只能分配给一个人，每个人只能执行一个任务。
第i个人执行第j个任务的成本是c[i][j]（1≤i，j≤n）。求出总成本最小的分配方案

解题思路

回溯法解题的一般步骤
（1）针对给定的问题确定问题的解空间树，问题的解空间树应至少包含问题的一个解或者最优解。
（2）确定结点的扩展搜索规则
（3）以深度优先的方式搜索解空间树，并在搜索的过程中可以采用减枝函数来避免无效搜索。其中，深度优先方式可以选择递归回溯或者迭代（非递归）回溯

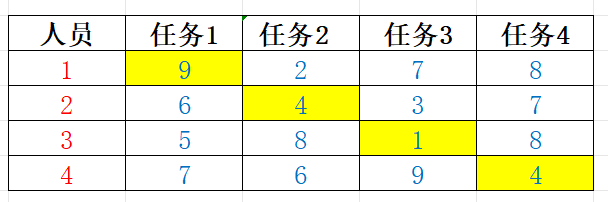
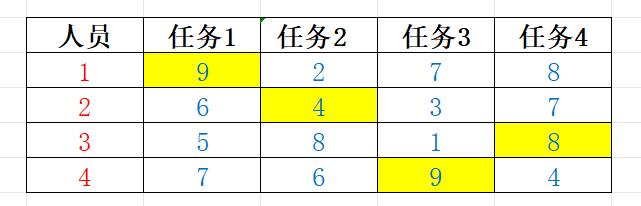
通过将问题进行适当的转化，得出解空间树为排列树，这棵树每条完整路径都代表了一种解的可能。通过深度优先搜索这棵树，枚举每种可能的解的情况，找出能得到最小的花费结果。其中构造约束函数，可以删除一些不可能的解，从而大大提高程序效率

算法描述

（1）解空间
解空间为{x1，x2，x3，x4……，xn}，其中xi=1，2，3，4……n，表示第i个人安排的任务
（2）解空间树

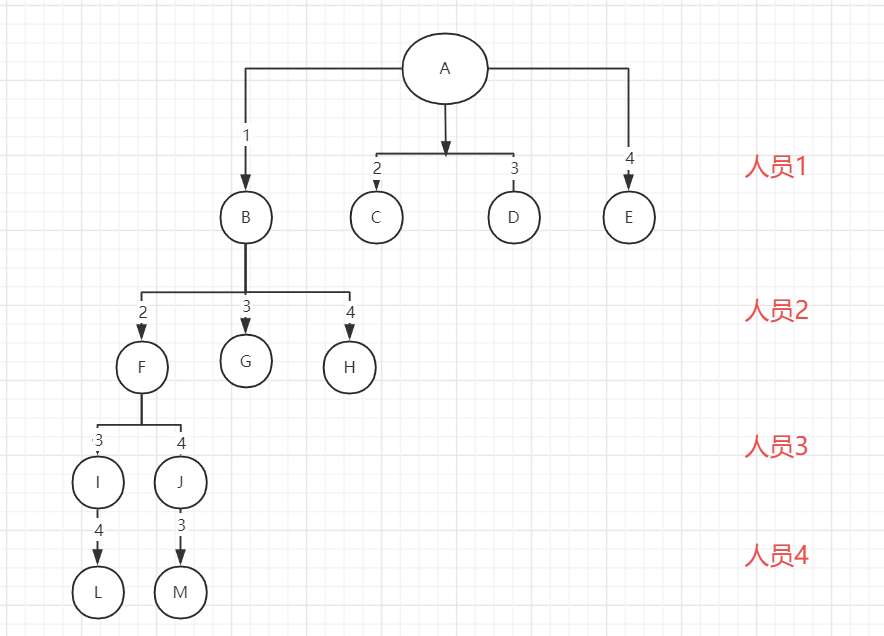
#include<stdio.h>
#include<cstring>
#include<queue>

using namespace std;
#define MAXN 20		
#define INF 9999
//问题表示： 
int n=4;//人或任务个数 
int c[MAXN][MAXN]={{0,0,0,0,0},{0,9,2,7,8},{0,6,4,3,7},{0,5,8,1,8},{0,7,6,9,4}}; 
//求解结果表示： 
int x[MAXN]; 		//临时解
int cost=0;			//临时解的成本
int bestx[MAXN];	//最优解
int mincost=INF;	//最优解成本
bool worker[MAXN]; 	//表示任务是否已经分配人员 

void dfs(int i)		//为第i个人员分配任务 
{
	if(i>n)			//如果达到叶子节点 
	{
		if(cost<mincost)		//当前成本小于最小成本mincost
		{mincost=cost;			//更新最小成本
		for(int j=1;j<=n;j++)	//遍历所有人员编号1~n
			bestx[j]=x[j];		//将最佳人员编号给bestx
		}
	}
	else{
		for(int j=1;j<=n;j++)	//遍历所有人员编号1~n
		if(!worker[j])			//如果没有分配任务
		{
		worker[j]=true;			//标记已经分配任务
		x[i]=j;					//将任务编号j分配给第i个人
		cost+=c[i][j];			//更新成本，加上分配任务成本
		dfs(i+1);				//调用dfs函数，分配下一个人员
		worker[j]=false;		//标记该人员未分配任务
		x[j]=0;					//任务编号清零，表示该人员未被分配任务
		cost-=c[i][j];			//更新当前成本，减去分配任务成本
	} 
 } 
}
int  main()
 {
 	memset(worker,0,sizeof(worker));				//memset函数将worker数组的所有元素初始化为0。
 	dfs(1);											//寻找最优方案
 	printf("最优方案\n");
 	for(int k=1;k<=n;k++)							//从1循环到总人数n
 		printf("第%d个人安排任务%d\n",k,bestx[k]);	//输出第k个人的任务分配
 	printf("总成本=%d\n",mincost);					//输出最小成本
 	return 0;
 }