索引介绍
索引是一种用于快速查询和检索数据的数据结构,其本质可以看成一种排序号的数据结构。
索引的作用相当于书的目录。打个比方:在查字典的时候,如果没有目录,那我们就只能一页一页地去查,速度很慢。如果有目录,我们只需要先去目录里查找字的位置,然后直接翻到那一页就行了。
索引底层数据结构存在很多种类型,常见的索引结构有:B树、B+树、Hash、红黑树。在 MySQL 中,无论是 Innodb 还是 MyIsam ,都使用了 B+树 作为索引结构。
索引的优缺点
优点:
- 使用 索引 可以大大加快数据的检索速度(大大减少检索的数据量)
- 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性
缺点:
- 创建索引和维护索引需要耗费很多时间。当对表中的数据进行增删改查的时候,如果数据有索引,那么索引也需要动态的修改,会降低 SQL 执行效率。
- 索引需要使用物理文件存储,也会耗费一定空间
索引底层数据结构
Hash 表
哈希表是键值对的集合,通过 键 即可快速取出对应的 值,因此哈希表可以快速地检索数据(接近O(1))。
# 构造散列函数
def hash(a):
return (a % 8) ^ 7类似的hash算法如上,通过异或或者移位的方式使得计算结果的规律性不那么明显,增加 hash 算法的可靠性
但是,哈希算法有一个 hash冲突 的问题,也就是说多个不同的 key(a) 最后得到的 index 可能相同。通常情况下,解决办法是 链地址法 ,即将哈希冲突的数据存放在链表中。
HashMap 就是一种常见的 采用 hash 表存储数据的结构(下图为jdk1.8之前的版本,jdk1.8之后的版本在此基础上加入了 红黑树 来解决链表过长带来的查询缓慢问题)
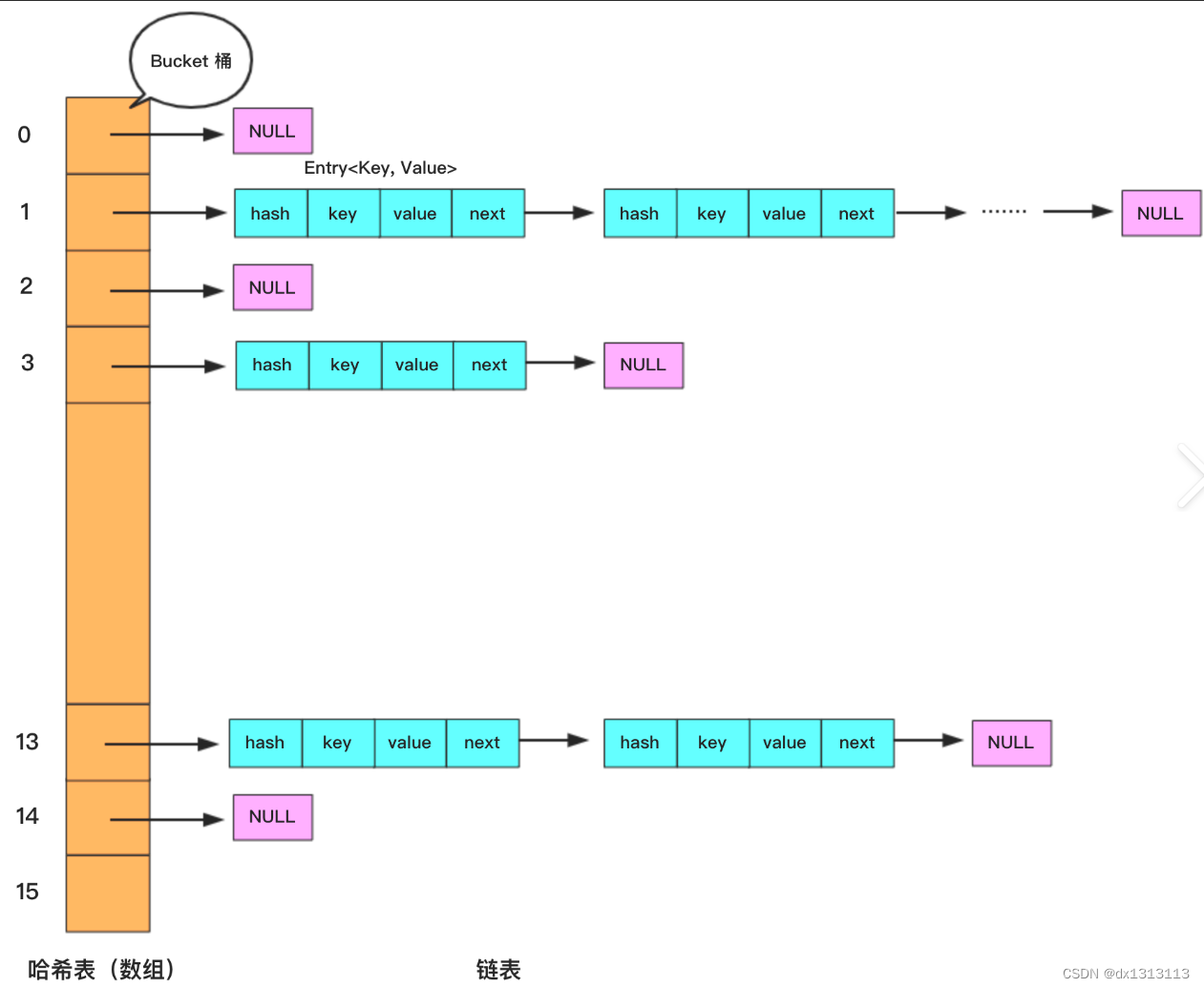
既然 哈希表 这么快,为什么 MySQL 没有使用其作为索引的数据结构呢?
主要是因为 Hash 索引是无序的,不支持顺序和范围查询。假如我们需要对表中的数据进行排序或者范围查询的时候,Hash 索引就不可行了。并且每次 IO 只能取一个。
SELECT * FROM tb1 WHERE id < 500;
在这种范围查询中,直接遍历比500小的叶子节点就够了。而使用 Hash 索引是根据 hash 算法来定位的,不能确保 存储的顺序。
二叉查找树(BST)
二叉查找树 是一种基于二叉树的数据结构,有以下特点:
- 左子树的所有节点的值均小于根节点的值
- 右子树的所有节点的值均大于根节点的值
- 左右子树页分别为二叉查找树
当二叉查找树是平衡的时候,也就是树的每个节点的左右子树深度相差不超过 1 的时候,查询的时间复杂度为 O(log2(N)),具有比较高的效率。然而 ,当二叉查找树不平衡时,例如在最坏情况下(有序插入节点),树会退化成线性链表(也称为斜树),导致查询效率急剧下降,时间复杂度退化为 O(N)
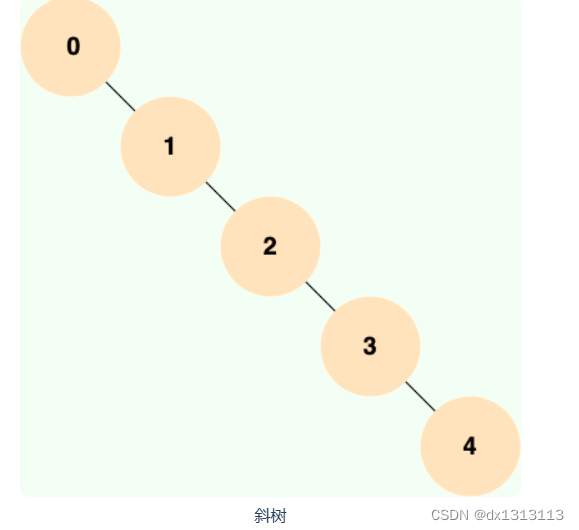
二叉查找树的性能非常依赖于它的平衡度,这就导致其不适合作为 MySQL 底层索引的数据结构。
AVL树 (平衡二叉树)
AVL树的特点是保证任何节点的左右子树高度之差不超过 1 ,因此也被称为高度平衡二叉树,它的查找、插入和删除在平均和最坏情况下的时间复杂度都是 O(logn)。
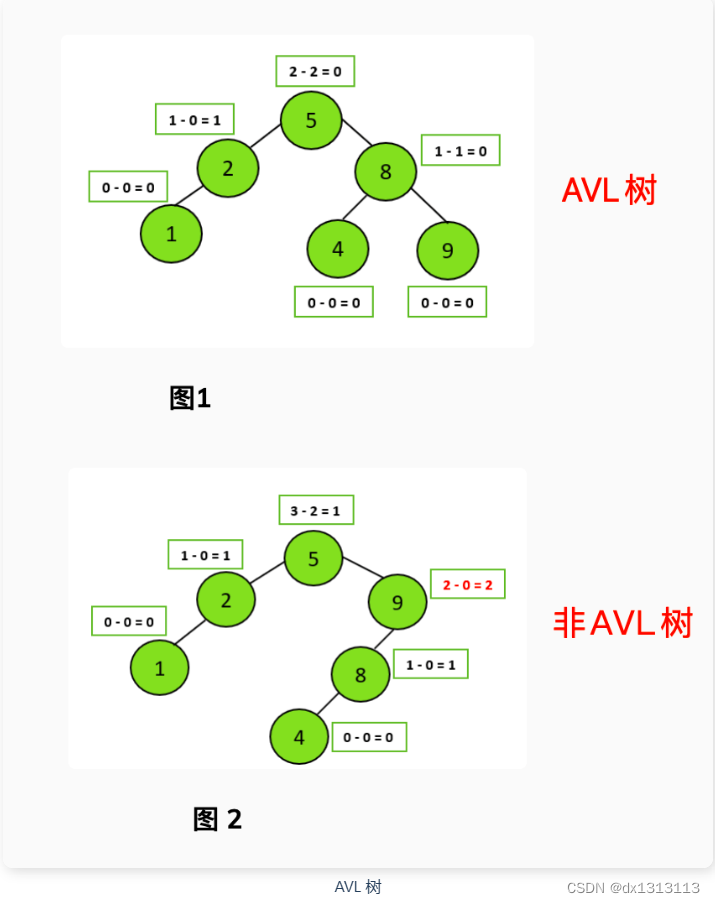
AVL树采用了旋转操作来保持平衡。主要有四种旋转操作:LL旋转、RR旋转、LR旋转和RL旋转。其中LL旋转和RR旋转分别用于处理左左和右右失衡,而LR旋转 和 RL旋转 用于处理左右和右左失衡。

由于 AVL 树需要频繁地进行旋转操作来保持平衡,因此会有较大的计算开销进而降低了查询的性能。并且,在使用 AVL 树时,每个树节点仅存储一个数据,而每次进行磁盘 IO 时只能读取一个节点的数据,如果需要查询的数据分布在多个节点上,那么就需要进行多次磁盘 IO。磁盘IO是一项耗时的操作,在设计数据库索引时,我们需要优先考虑如何最大限度地减少磁盘 IO 操作的次数。
除此之外,随着数据的增多,树的高度也会变高,这就意味着磁盘 IO 操作次数增多,会影响整体数据查询的效率。
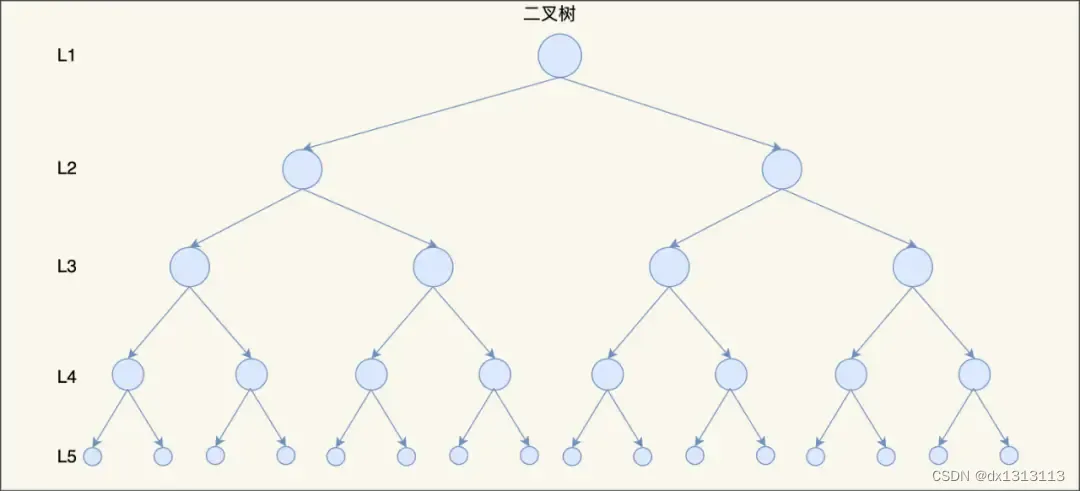
比如,上图的平衡二叉树的高度为 5 ,那么在访问最底部的节点时,就需要 5 次 磁盘 IO 操作。根本原因是因为它们都是二叉树,也就是每个节点只能保存两个子节点
B 树
AVL 树虽然能保持查询操作的时间复杂度在 O(logn),但是因为它本质上是一个二叉树,每个节点只能存储 2 个子节点,那么当节点个数越多的时候,树的高度也会相应变高,这样就会增加磁盘的 IO次数,从而影响数据查询的效率。
为了解决降低树的高度的问题,就引出了 B 树,它不再限制一个节点只能有 2 个 子节点,而是允许 M 个子节点,从而降低 树的高度。
假设 M = 3 ,那么就是一颗 3 阶的 B 树,特点就是每个节点最多有 2 个 (M-1个)数据和最多有 3 个(M 个)子节点,超过这些要求的话就会分裂节点:

假设我们在下面这幅 B 树中查找的索引值是 9 的记录
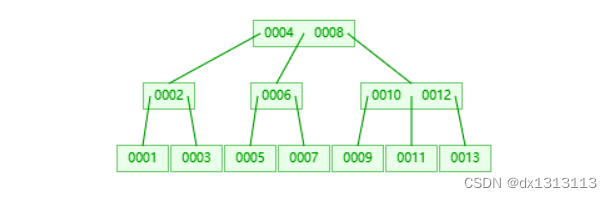
那么步骤可以分为以下几步:
- 与根节点的索引(4,8)进行比较,9 > 8 所以查询最右边的子节点
- 然后该子节点的索引为 (10,12),9 < 10 所以查询该节点的最左边的子节点
- 找到索引值为 9 的节点。
可以看到 ,一颗 3 阶的 B 树在查询叶子节点中的数据时,由于树的高度是 3 ,所以在查询过程中会发生 3 次磁盘 IO 操作。
而同样的数据放在平衡二叉树下,树的高度就会很高,意味着磁盘 IO 操作会更多。所以 B 树在数据查询中比平衡二叉树的效率高。
但是 B 树的每一个节点都包含数据(索引 + 记录) ,而用户的记录数据的大小很有可能远远超做过了索引数据,这就需要花费更多的 磁盘 IO 操作次数来读到 有用的索引数据。
而且在我们查询位于叶子节点上的数据的时候,其父节点以及之前的节点的数据也会加载到磁盘内存,但是这些数据时没有用的,我们只想获取最终节点上的数据,而不是查询过程中遍历过的节点的数据。所以使用 B 树作为索引的话会占用大量内存资源(这些资源本不应该被占用)
另外,如果使用 B 树来做范围查询的话,需要使用中序遍历,这会涉及到多个节点的磁盘 IO 问题一,从而导致整体速度下降。
B+树
B+树就是对 B 树做了一个升级,MySQL 中索引的数据结构就是采用的 B+树:
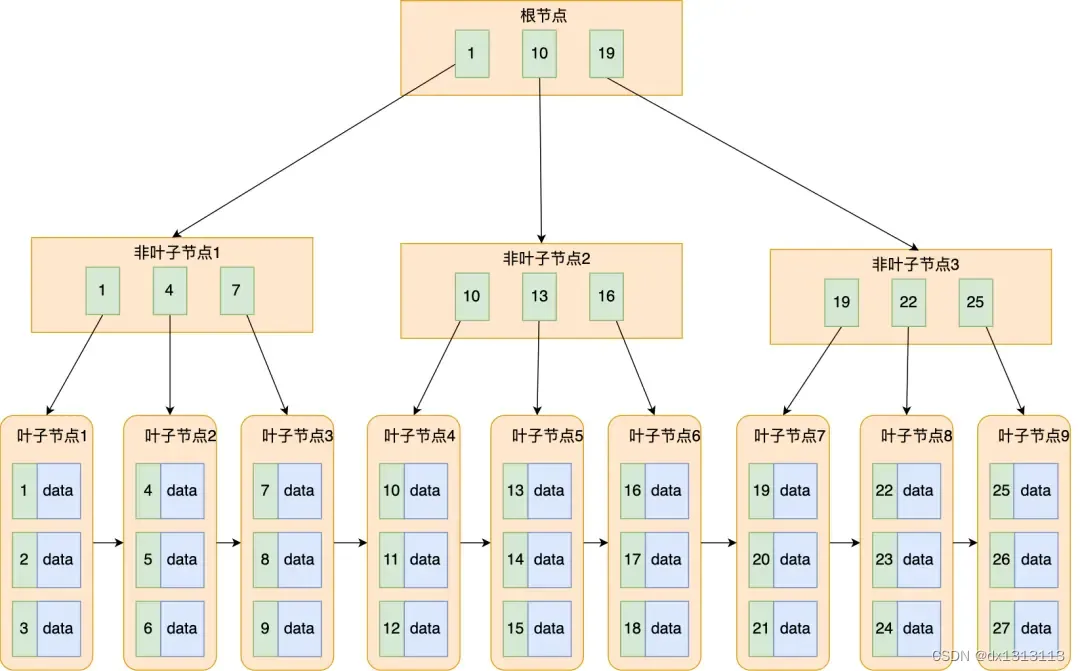
B+树和 B 树差异的点,主要是以下几个点:
- 叶子节点才会存放实际数据,非叶子节点只能存放索引
- 所有索引都会在叶子节点出现,叶子节点之间构成一个有序链表(在mysql中是双向链表)
- 非叶子节点的索引会同时存在于子节点中,并且是在子节点中最大或者最小
- 非叶子节点中有多少个子节点,就有多少个索引
查询效率:
B+树的非叶子节点不存放实际的记录数据,仅存放索引,因此数据量相同的情况下,相比存储索引又存储记录的 B 树, B+树的非叶子节点可以存放更多的索引,因此 B+ 树可以比 B 树更 [矮胖] ,查询底层节点的磁盘 IO 次数会更少。
插入和删除效率:
B+ 树有大量的冗余节点,这导致删除一个节点的时候,可以直接从叶子节点中删除,甚至不需要动非叶子节点。
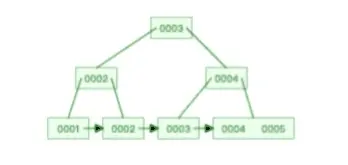
B+ 树的插入操作也是一样,由于有冗余节点,插入可能存在节点的分裂(节点饱和的话)但是最多只涉及树的一条路径。而且 B+树会自动平衡,不需要做更多复杂的操作
范围查询:
由于 B+树所有的叶子节点搜集通过链表进行连接,这种设计可以帮助我们更直接地获取范围内的数据,直接遍历链表即可,而不需要像B树那样,去遍历树。
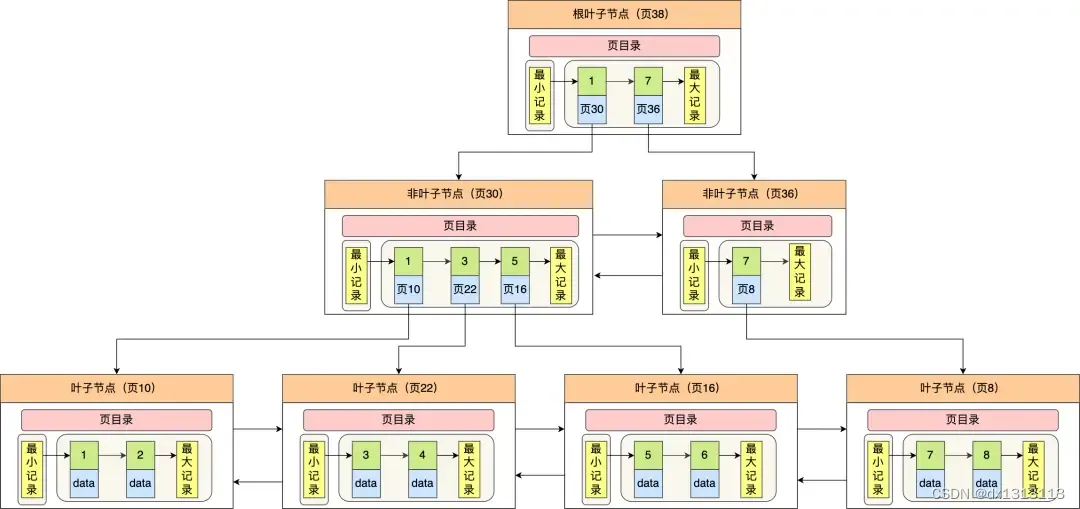
在 Mysql 中 innoDB 存储引擎采用的就是 B+树作为索引的数据结构,但是在其基础上加了些改进:
- InnoDB存储引擎中 叶子节点是通过双向链表进行连接的,这使得范围查询更加方便,既能向右遍历也能向左遍历
- B+ 树的节点内容是数据页,数据页中存放了用户的记录以及各种信息,每个数据页的大小默认是 16KB
总结
二分查找树虽然是一个天然的二分结构,能很好的利用二分查找快速定位数据,但是它存在一种极端的情况,每当插入的元素都是树内最大的元素,就会导致二分查找树退化成一个链表,此时查询复杂度就会从 O(logn)降低为 O(n)。
了解决二分查找树退化成链表的问题,就出现了自平衡二叉树,保证了查询操作的时间复杂度就会一直维持在 O(logn) 。但是它本质上还是一个二叉树,每个节点只能有 2 个子节点,随着元素的增多,树的高度会越来越高。
而树的高度决定于磁盘 I/O 操作的次数,因为树是存储在磁盘中的,访问每个节点,都对应一次磁盘 I/O 操作,也就是说树的高度就等于每次查询数据时磁盘 IO 操作的次数,所以树的高度越高,就会影响查询性能。
B 树和 B+ 都是通过多叉树的方式,会将树的高度变矮,所以这两个数据结构非常适合检索存于磁盘中的数据。
但是 MySQL 默认的存储引擎 InnoDB 采用的是 B+ 作为索引的数据结构,原因有:
- B+ 树的非叶子节点不存放实际的记录数据,仅存放索引,因此数据量相同的情况下,相比存储即存索引又存记录的 B 树,B+树的非叶子节点可以存放更多的索引,因此 B+ 树可以比 B 树更「矮胖」,查询底层节点的磁盘 I/O次数会更少。
- B+ 树有大量的冗余节点(所有非叶子节点都是冗余索引),这些冗余索引让 B+ 树在插入、删除的效率都更高,比如删除根节点的时候,不会像 B 树那样会发生复杂的树的变化;
- B+ 树叶子节点之间用链表连接了起来,有利于范围查询,而 B 树要实现范围查询,因此只能通过树的遍历来完成范围查询,这会涉及多个节点的磁盘 I/O 操作,范围查询效率不如 B+ 树。