1、数字数据压缩编码基本原理
数据分为数字数据和模拟数据,此处的数据指的是数字数据或数字化后的模拟数据
(1)数字数据压缩编码要求
数据与语音或图像不同,对其压缩是不允许有任何损失,只能采用无损压缩的方式。压缩编码选用一种高效的编码表示信源数据,以减小信源数据的冗余度,即减小其平均比特数。并且,这种高效编码必须易于实现和能逆回原信源编码。
(2)熵编码
信源的熵的定义,表示信源中每个符号所含信息量的统计平均值。减小信源数据的冗余度,相当于增大信源的熵。编码称为熵编码
(3)信源字符表
一个有限离散信源可以用一组不同字符xi(i=1,2,……,N)的集合X(N)表示。X(N)称为信源字符表,表中的字符为x1,x2,……,xn。信源字符表可以是二进制的,也可使多字符的,非二进制字符可以通过一个字符编码表映射为二进制码字。标准的字符二级制码字是等长的
(4)等长码和变长码
等长码中表示每个字符的码字长度是相同的,但是各字符所含有的信息量是不同的。含信息量小的字符的等长码字必然有更多的冗余度。
为了压缩,通常采用变长码。变长码中每个码字的长度是不等的,字符的码长反比于此字符出现的概率。当多有字符以等概率出现时,编码才是等长的。
等长码可以通过计数的方法确定字符的分界,但变长码则不可以,接收端收到一长串变长码,不一定能确定每个字符的分界。
为了压缩数据,常采用变长码,以求获得高的压缩效果,常见编码方式有霍夫曼(Huffman)编码、香农-费诺编码等
2、霍夫曼编码(Huffman)
霍夫曼编码是一种无前缀变长码。对于给定熵的信源,霍夫曼编码能得到最小平均码长。在最小码长意义上,霍夫曼编码是最佳编码,也是效率最高的编码。
(1)一个霍夫曼编码的示例
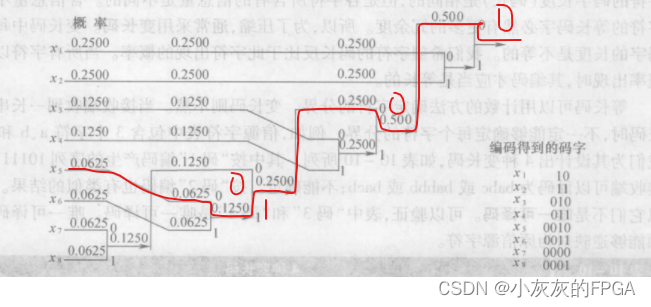
以8个字符的信源字符表来说明下霍夫曼编码的编码方式
设信源的输出字符为x1,x2,x3,x4,x5,x6,x7,x8
对应概率分别为
P(x1)=P(x2)=1/4
P(x3)=P(x4)=1/8
P(x5)=P(x6)=P(x7)=P(x8)=1/16
采用霍夫曼编码的过程
①将8个字符按照概率不增大的次序排序
②将概率最小的两个信源字符x7和x8合并,将x7分配二进制“0”作为其码字的最后一个码元;x8分配二进制“1”作为其码字的最后一个码元
③x7和x8合并后的复合字符的概率为P(x7)+P(x8)=1/8,并将新得到一组字符按照概率不增大的次序排列,注意:新复合字符与x3和x4概率相同,可放置在x2和x5之间的任何位置,此例子放置在x4之后,替换x5;
④将排序后的x6和x7合并,按照概率不增大的次序排列;
⑤最终得到一个下述的树状图;
⑥从树的最右端向左追踪,即可得到编码输出码字
以x5的码字获得来描述下,图中红线为x5的路径,从树的最右端向左追踪可得到编码为0010;其余类似
(2)压缩比和编码效率
用压缩比和编码效率来反映压缩编码性能的指标
压缩比是压缩前(采用等长码)每个字符的平均码长与压缩后每个字符的平均码长之比
编码效率等于编码后的字符平均信息量(熵)与编码平均码长之比
以上述霍夫曼编码示例来计算
若采用等长码对信源字符编码,由于存在8(2^3)种字符,故码长为3
编码后的字符平均信息量(熵)的计算
H(x)=
P(x1)[-log2(P(x1))]+P(x2)[-log2(P(x2))]+
P(x3)[-log2(P(x3))]+P(x4)[-log2(P(x4))]+
P(x5)[-log2(P(x5))]+P(x6)[-log2(P(x6))]+
P(x7)[-log2(P(x7))]+P(x8)[-log2(P(x8))]
=2×1/4×[-log2(1/4)]+2×1/8×[-log2(1/8)]
+4×1/16×[-log2(1/16)]
= 2.75(b)
编码平均码长
n1×P(x1)+n2×P(x2)+n3×P(x3)+n4×P(x4)+
n5×P(x5)+n6×P(x6)+n7×P(x7)+n8×P(x8)
=2×0.25+2×0.25+3×0.125+3×0.125
+4×0.0625+4×0.0625+4×0.0625+4×0.0625
=2.75
故压缩比=
(压缩前(采用等长码)每个字符的平均码长)/压缩后每个字符的平均码长
=3/2.75=1.09
编码效率=
(编码后的字符平均信息量(熵))/(编码平均码长)
=2.75/2.75=100%
通信原理板块——数字数据压缩编码之霍夫曼编码
news2026/3/13 0:49:18
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1114399.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
微信好友消息自动回复,让你轻松应对好友咨询
有许多用微信做业务、做微商的小伙伴,微信有时候消息太多看不过来,漏看消息,或者不知道怎么引导用户,让他们看到你想让他们看到的消息。微信上用户多微信上的信息容易漏掉,怎么能有时效的回复客户呢?此时你…
Mybatis-plus连接postgrel数据库主键自增问题
首先pg中没有直接设置主键自增这一说法,一般只能新建一个序列,可以使用Navicat创建 在mp的配置类中加入序列的配置:
Bean
public IKeyGenerator keyGenerator() {return new H2KeyGenerator();
}然后实体类的主键策略只能是INPUT࿰…
MathType7.4最新免费版(公式编辑器)下载安装包附安装教程
MathType是一款专业的数学公式编辑器,理科生专用的必备工具,可应用于教育教学、科研机构、工程学、论文写作、期刊排版、编辑理科试卷等领域。可视化公式编辑器轻松创建数学方程式和化学公式。兼容Office Word、PowerPoint、Pages、Keynote、Numbers 等7…
WINCC趋势画面模板
加载按钮
Sub OnClick(Byval Item) Dim Chart,tag,ctrl,objTrendWnd,objTimeAxis,objValAxis,objTrendSet ChartScreenItems("组合框2")Chart
tagChart.SelTextSet ctrl ScreenItems("控件1")threadSet objTrend…
为什么说99%的传统视频监控都有问题?
就传统的监控来说,主要还是通过摄像头单纯地记录画面,依赖人力在屏幕前“看”,工作人员长时间盯着十几个监控画面,十分容易疲劳导致注意力不集中,不能及时发现事故并解决。而且传统的视频监控仍以事后查证为主…
网上可以赚钱的软件,闲暇时间可用来薅羊毛做副业
正因为有了互联网,我们的生活变得越来越便利。我们可以在网上购物、休闲娱乐、与朋友交流,甚至可以通过网上做副业来赚取额外收入。生活中总会有一些业余时间,而很多人也不想浪费它,总想着做一点事情来弥补经济上的不足。因此&…
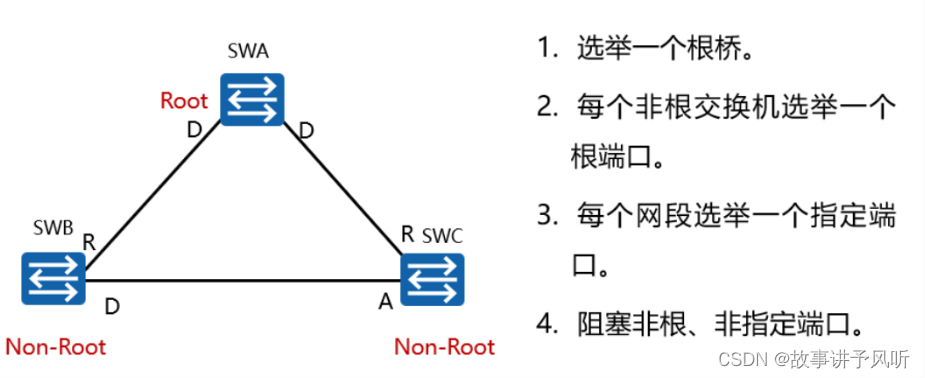
STP生成树协议详解
一、STP作用
如果链路断开或节点故障,那么互联的设备就无法正常通信了,这类网络问题叫做单点故障。没有备份的链路或节点,出现故障会直接断网。如果要提供 724 小时不间断的服务,那就需要在网络中提前部署冗余。避免出现单点故障…
web站点的欢迎页面
2023.10.20
什么是一个web站点的欢迎页面? 当我们设置了欢迎页面之后,在访问这个webapp的时候,或者访问这个web站点的时候,没有指定任何“资源路径”,这个时候会默认访问你的欢迎页面。
如何设置欢迎页面?…
Python基础教程:行与缩进正确用法教程
嗨喽,大家好呀~这里是爱看美女的茜茜呐 缩进
使用缩进来表示代码块,不需要使用大括号 {} 。
同一个代码块的语句必须包含相同的缩进空格数。
if True:print ("Answer")print ("True")
else:print ("Answer")print (&qu…
【EI会议征稿】第三届应用力学与先进材料国际学术会议(ICAMAM 2024)
第三届应用力学与先进材料国际学术会议(ICAMAM 2024)
2024 3rd International Conference on Applied Mechanics and Advanced Materials(ICAMAM 2024) 第三届应用力学与先进材料国际学术会议(ICAMAM 2024)…
【Andriod】SDK下载安装及环境配置完整教程
文章目录 1.Android SDK下载2.Android SDK安装3.Android SDK的配置4. Android SDK的环境变量配置(win 10) 1.Android SDK下载 目前官网上已经没有单独的SDK下载安装包了。谷歌官网推荐的是下载包含有Android SDK的Android Studio。官网下载地址 如下图,选择对应的系…
三江学院“火焰杯”软件测试高校就业选拔赛颁奖仪式
11月25日下午,“火焰杯”软件测试开发选拔赛及三江-慧科卓越工程师班暑期编程能力训练营颁奖仪式在s楼会议室隆重举行。计算机科学与工程学院院长刘亚军、副院长叶传标、曹阳、吴德、院党总支副书记王兰英、系主任杨少雄、慧科企业代表尹沁伊人、项目负责人王旭出席…
支持录音的笔记APP,可将录音转化为文字的笔记软件
提及笔记APP工具,无外乎是电子笔记和手写笔记,现如今随着科技的不断发展,人们使用电子设备的频率是越来越多,在选择笔记APP时,大家不想再单纯的依靠手动输入文字记录,反而更多的是喜欢快捷的录音添加笔记的…
Android 指定有线网或Wifi进行网络请求
Android 指定有线网或Wifi进行网络请求 文章目录 Android 指定有线网或Wifi进行网络请求一、前言:二、指定网络通讯测试1、 窗口命令 ping -I 网络节点 IP2、Java 代码指定特定网络通讯 三、指定特定网络的demo app 开发1、效果图:2、实际测试结果说明&a…
Unity中Shader的ShadowMapping的原理(阴影)
文章目录 前言一、阴影的作用1、阴影可以增加真实度2、阴影可以提升空间感 二、阴影的生成1、现实中阴影的生成2、Unity中阴影的生成 ShadowMapping 三、ShadowMapping原理1、在 光源处添加一个相机,同时打开深度测试 与 写入,并生成ShadowMap࿰…
用echarts在vue2中实现3d饼图
先看效果,再看文章: 一、安装插件
3d的图不仅用到echarts,还用到了echarts-gl,因此都需要安装一下哦~
npm install echarts
npm install echarts-gl2.0.9 //可以指定版本,也可不指定二、在main.js中引入
import * …
PixCakeAI人像处理技术修图软件:打造你的完美像素之境
在当今这个数字时代,我们的形象,无论是在社交媒体上,还是在日常生活中,都显得尤为重要。有没有想过,你可以自己动手,轻松打造出独一无二的像素艺术作品?现在,让我们一同探索一个全新…
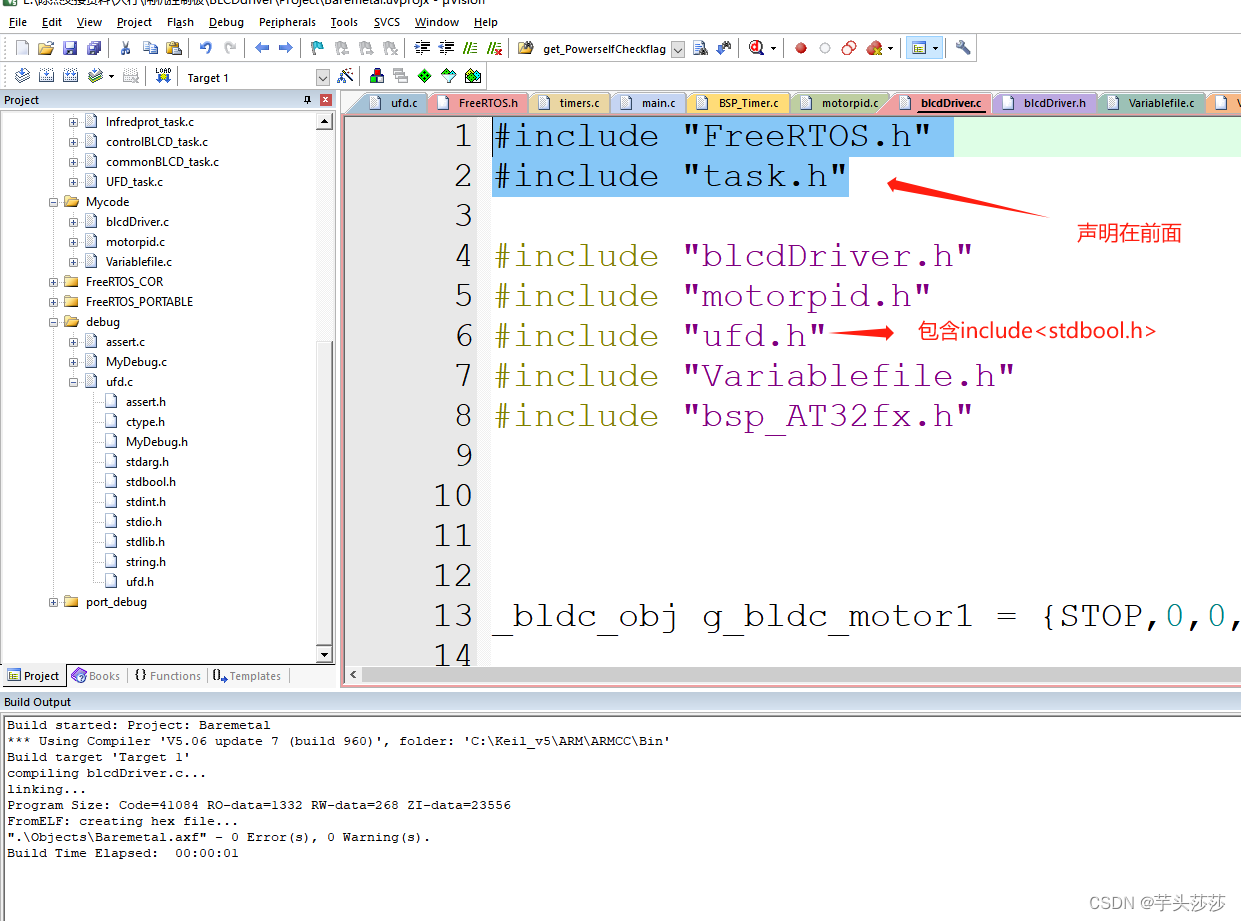
..\FreeRTOS\include\FreeRTOS.h(1277): error: #65: expected a “;“出现的这个错误标志解决方法
..\FreeRTOS\include\FreeRTOS.h(1277): error: #65: expected a ";"
近来写软件过程中,当在某一个.C文件中我申明了FreeRTOS.h文件,结果呢编译是出现报错了 经过查找,是因为我在另外一个文件声明了 #include <stdbool.h> …