原文链接:
https://github.com/mit-han-lab/amc/security
https://zhuanlan.zhihu.com/p/108096347
https://zhuanlan.zhihu.com/p/510905067
摘要
结论:
1、deep compression:由三阶段pipeline组成:pruning(剪枝)、 trained quantilization()、Huffman coding(哈夫曼编码)
2、通过deep compression,在不损失模型精度的前提下可以减少35-49倍的神经网络存储
3、首先通过学习神经网络的重要连接对网络进行剪枝,然后通过trained quantization 对剩下的connections进行量化。基于ImageNet数据集在网络AlexNet和VGG-16上进行试验,效果显著,提升了on-chip SRAM cache(静态随机存储)的使用,降低了off-chip DRAM memory(动态随机存储的使用)
4、同时使用 deep compression 技术使得复杂网络可以应用在移动端。同时能够加速和提高功耗利用率
一、引言

二、网络剪枝
网络剪枝被广泛研究应用在压缩CNN。最早是用来降低网络复杂度和防止过拟合。本文研究它用于无损精度压缩网络。
weight sharing(权值共享):权值共享是指学习到的局部信息可以应用到图像中的其他地方上去。例如用一个卷积核卷积整幅图像,每个卷积核在图像上是不断重复的,这些重复的卷积核共享着相同的参数设定(weights和bias)。
本文中权值共享的方案如下:
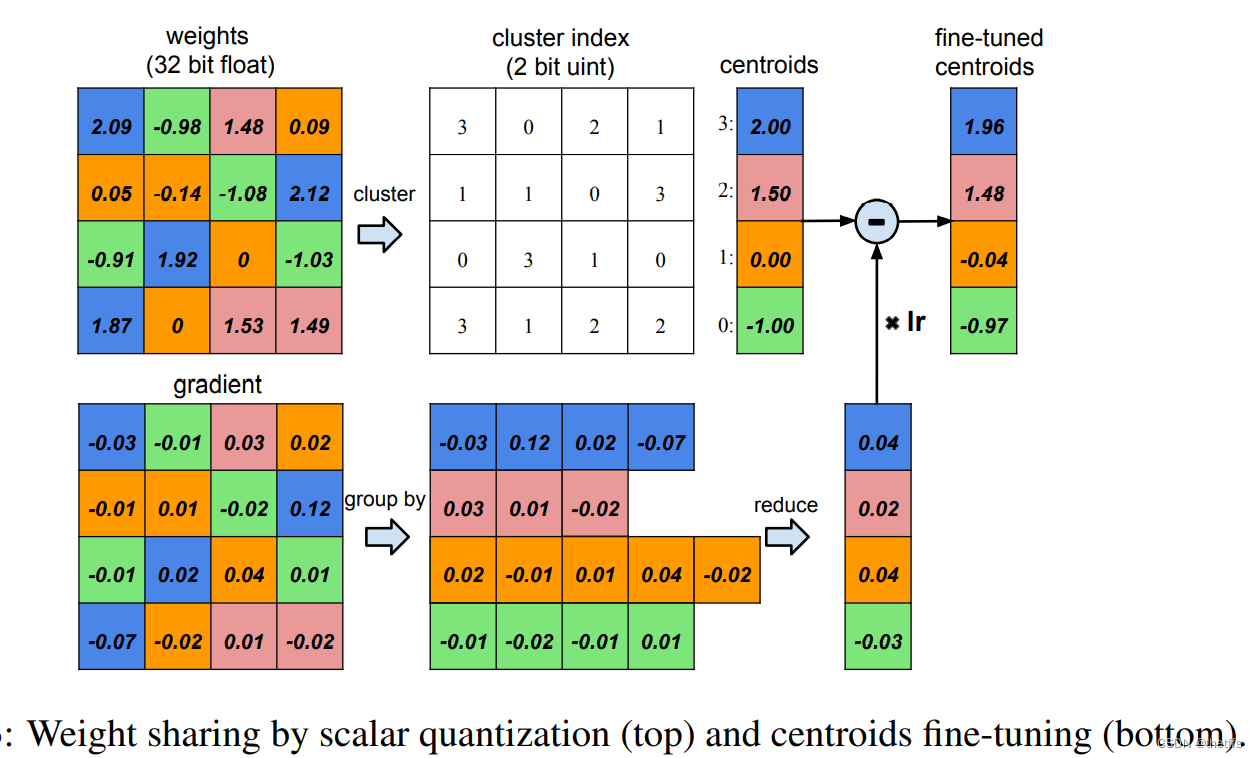
1、采用Compressed sparse row(CSR)或者 Compressed sparse column(CRC)存储剪枝后的稀疏矩阵
2、稀疏矩阵的存储至少需要2a + n + 1个存储单元,其中a表示非零元素的数量,n是行或者列的数量。
3、为了进一步压缩我们保存元素的相对索引,而不是坐标。对于conv层,采用8bit存储。对于fc层采用5bit存储
4、当相对索引的位置超出存储范围,如下图所示,我们采用0 padding的方法解决。
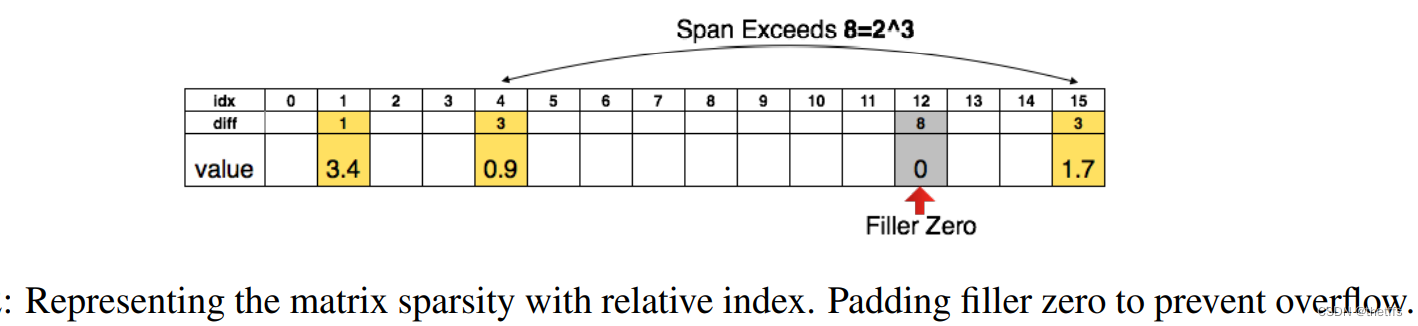
三、训练量化和权值共享
压缩率的计算公式:
为了衡量压缩率,对于k个cluster ,仅仅需要 log2(k)个bit存储索引。因此对于一个网络连接数是n,每个连接用b个bit表示,共享权值数量是k时,压缩率为:
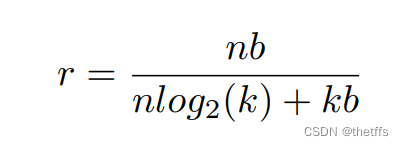
3.1权值共享
对训练网络的每一层采用K-means聚类算法进行权值共享,因此同一个簇中的权值是相同的,并且权值不在网络层之间共享,因此最小化簇内平方和的公式为:

3.2 初始化权值共享
本文比较了三种初始化权值共享的方法:Forgy(random)、density-based、linear。
Forgy:随机选择k个观察对象以及中心。如图所示,中心点分布较密集
density-based:基于CDF累积分布函数 (cumulative distribution function),在CDF曲线轨迹的线性空间选择中心点。如图,中心点分布较稀疏
linear:在原始权值的最大值和最小值中间选取中心点。如图中心点分布最稀疏。
结论:大权值比小权值影响力更大,但是同时它们的数量更少,因此在Forgy和density-based方法中,非常少的中心位于大权值处,因此不能很好的代表大权值。而linear初始化方法就没有这个问题。基于这三种方法进行聚类和fine-tune并测试准确性,实验表明linear初始化方法表现最好。
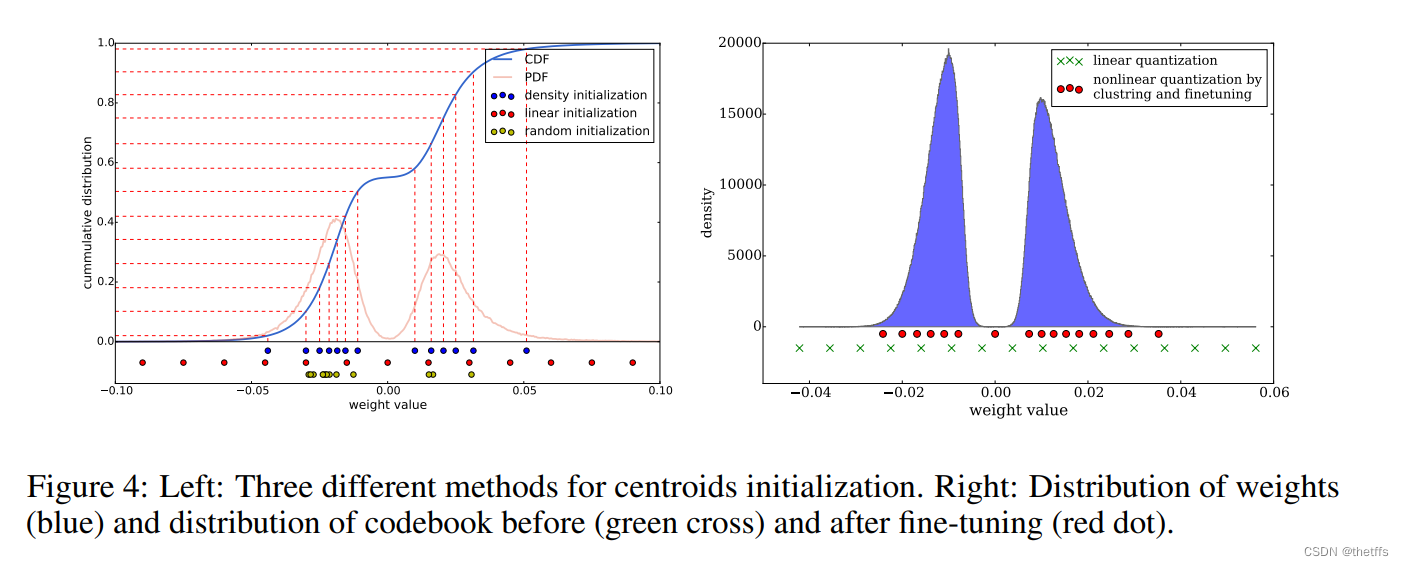
3.3 feed-forward(前馈)和反向传播
一维K-means聚类的中心即共享权值。feed-forward和反向传播的中间过程需要查找共享权值表。对于每个连接都保存了共享权值表的索引。在反向传播阶段计算每个连接的共享权值的梯度,并更新共享权值。该过程在上图中有展示。共享权值的梯度计算如下图所示。
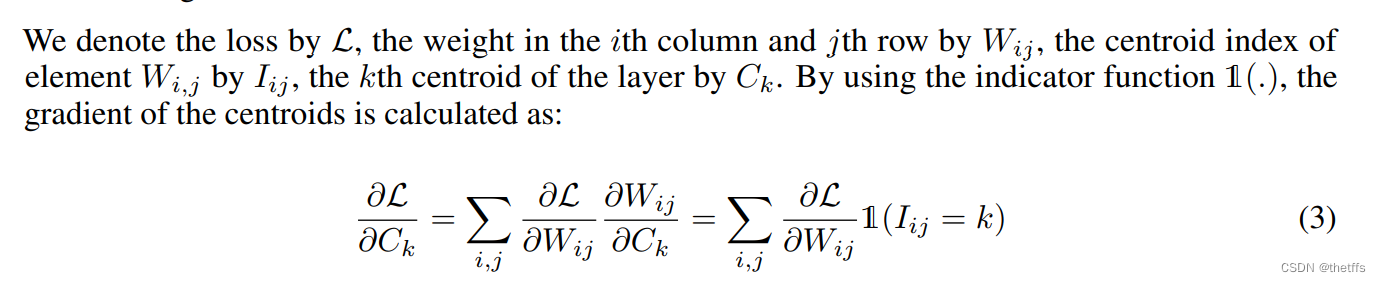
4、霍夫曼编码(Huffman code)
霍夫曼编码是一种用于数据无损压缩的最优的前缀码。它使用可变长的编码压缩源字符。根据字符出现的概率性成熟表,出现概率越高的字符,需要越短的编码来表示。
下图展示了AlexNet网络最后一层全连接层的量化权值和稀疏矩阵索引的概率分布图。两种分布均有偏差。量化权值分布集中在双峰,稀疏矩阵索引的分布插值几乎不超过20.实验表明使用霍夫曼编码存储这些非均匀分布数据,能够减少20%-30%的网络存储。
5、实验
5.1LeNet-300-100和LeNet-5 在Mnist数据集上的表现:
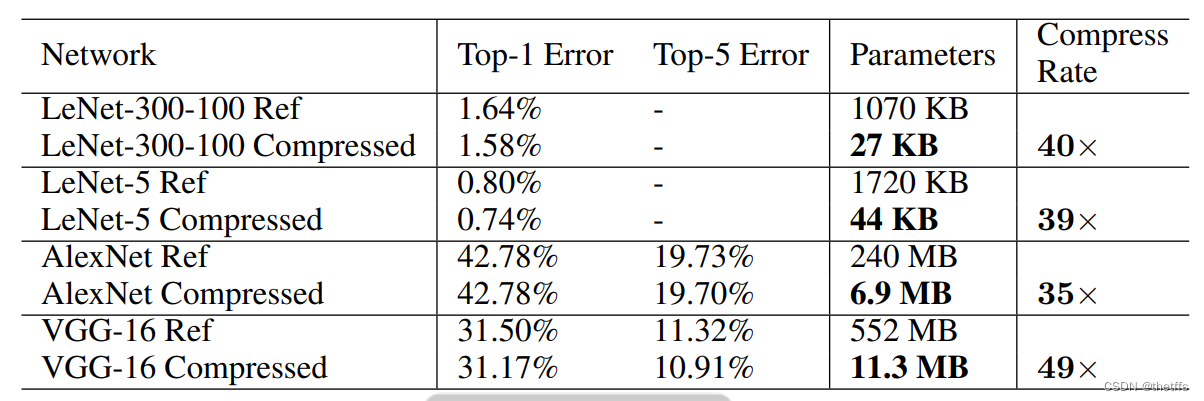
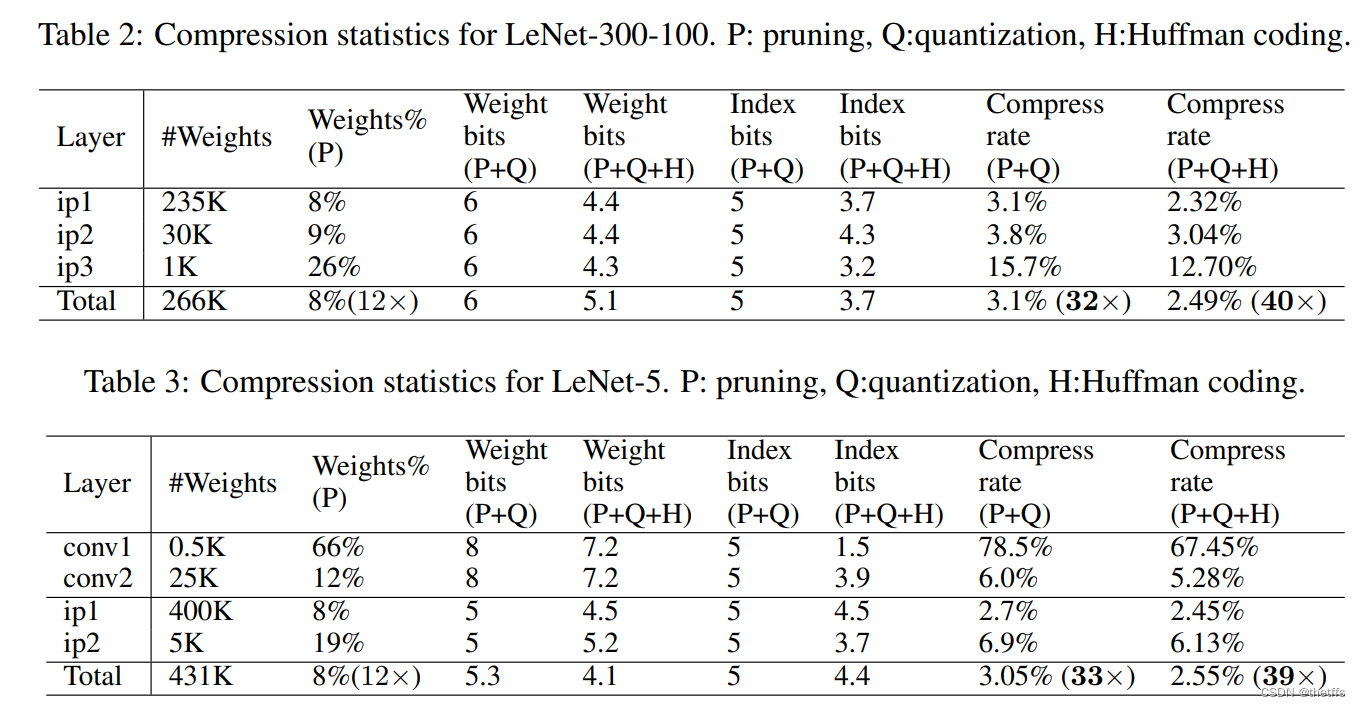
5.2 AleNet在 ImageNet ILSVRC2012数据集上的表现:
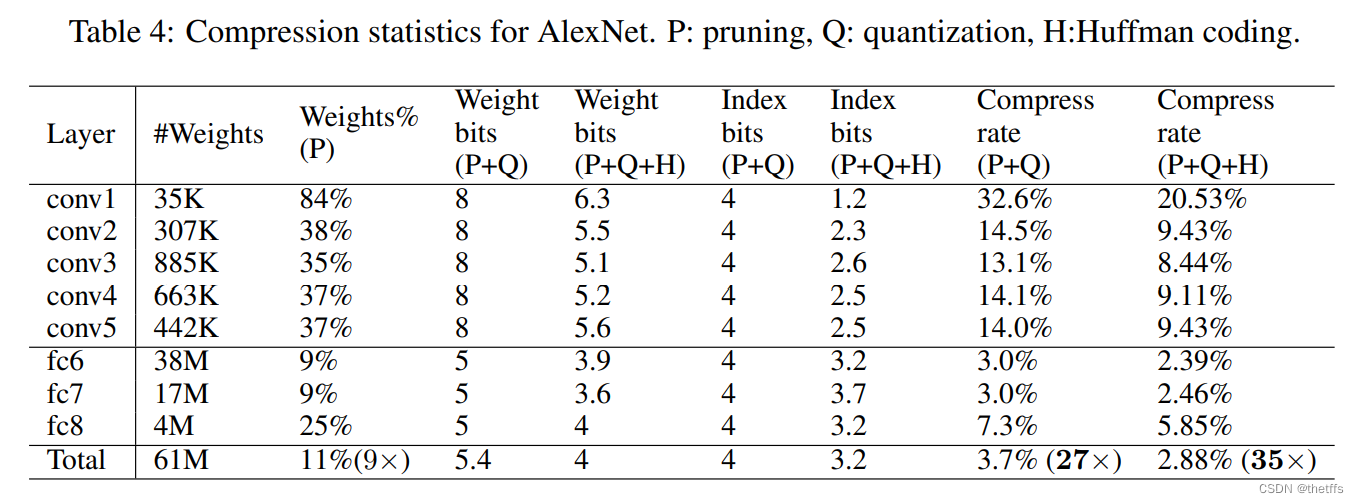
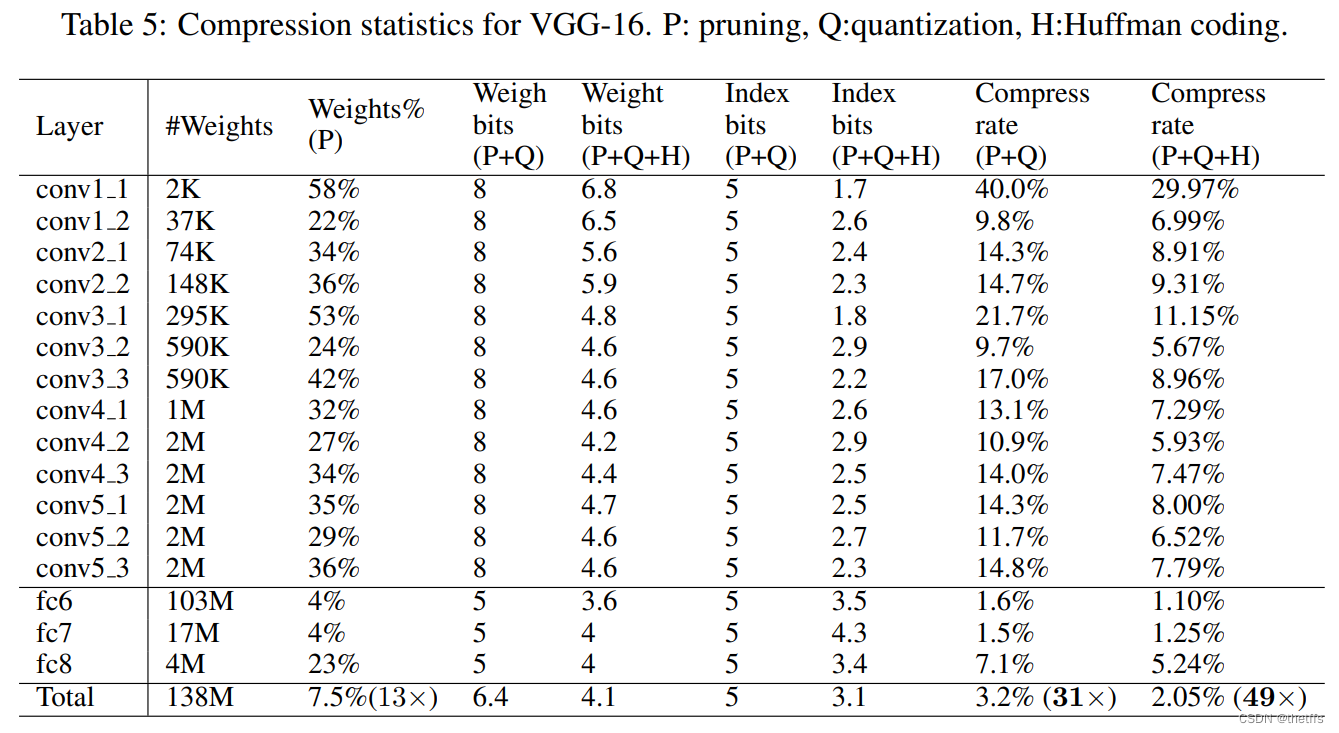
5.3 VGG-16 在ImageNet ILSVRC2012数据集上的表现:
6、论述
6.1 剪枝和量化协同作用
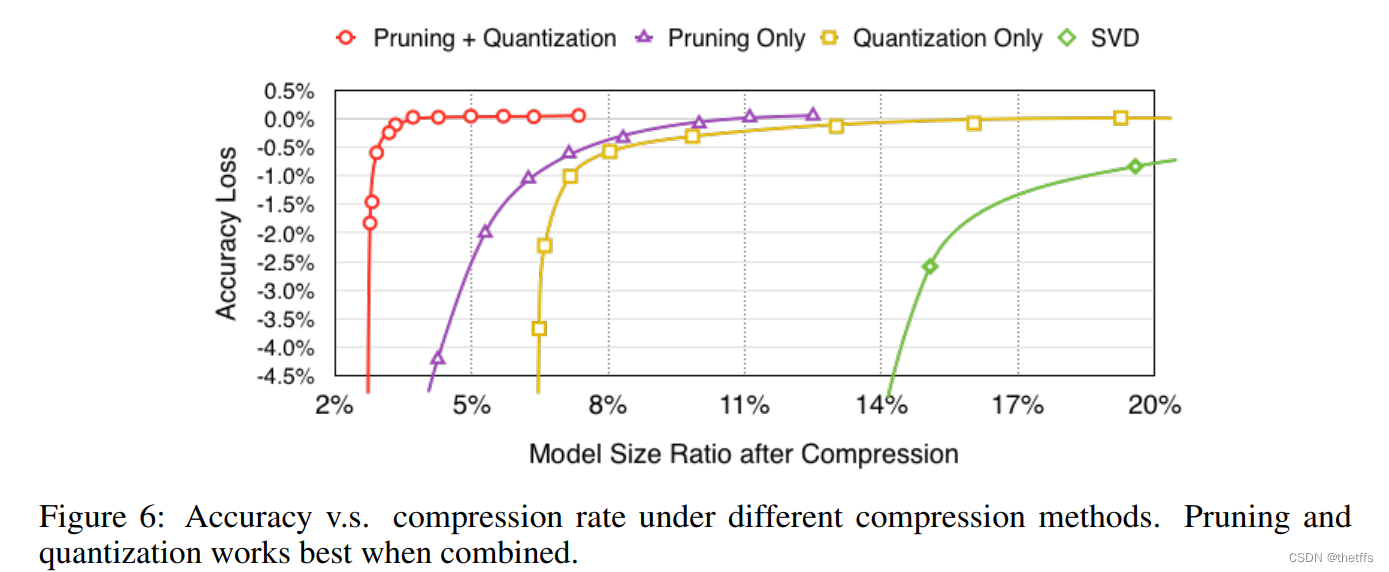
剪枝、量化作用在模型上,产生的压缩率及相应的精度损失绘制成曲线图,如下所示。实验结果表明剪枝和量化同时作用在模型上时,能获得最低的模型压缩率并且几乎没有精度损失。
SVD算法:奇异值分解算法可以实现降维,把数据集映射到低维空间中。数据集的特征值在SVD中用奇异值来表征,按照重要性排列,降维过程就是舍弃不重要的特征向量的过程,而剩下的特征向量组成的空间即为降维后的空间。
hica-stream 前期调研。分析竞品。
TS文档:输出调研文档
6.2 中心初始化
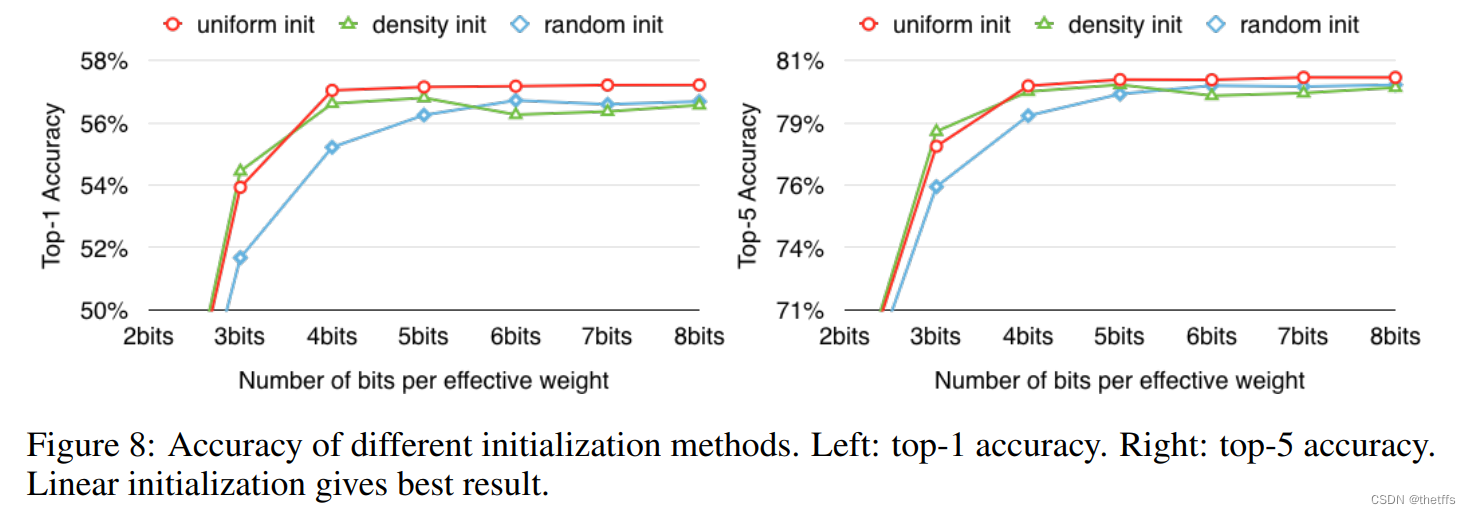
实验思路:用不同的bit位表示中心,并使用3.2小节提到的三种初始化中心的方法linear、density,forgy。得到在不同的bit数初始化中心下的top-1和top-5准确率如下图所示。图表明,除了在3bit初始化中心,linear方法的准确率均高于其他两种方法。
linear方法初始化中心优于其他两种方法的原理在3.2小节中说明了,此处不再赘述。
6.3