4.23 推导
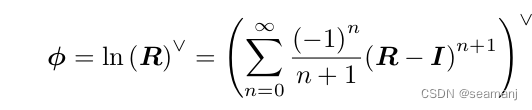
f
(
x
)
f(x)
f(x)在点a处的泰勒展开
f
(
x
)
=
∑
n
=
0
∞
f
(
n
)
a
n
!
(
x
−
a
)
n
f(x) = \sum_{n=0}^\infty \frac{f^{(n)}a}{n!}(x-a)^n
f(x)=∑n=0∞n!f(n)a(x−a)n
l
n
x
lnx
lnx的n阶导数
l
n
(
n
)
x
=
(
−
1
)
n
−
1
(
n
−
1
)
!
x
n
ln^{(n)}x = \frac{(-1)^{n-1}(n-1)!}{x^n}
ln(n)x=xn(−1)n−1(n−1)!
l
n
(
R
)
ln(R)
ln(R)在
I
I
I处展开
l
n
(
R
)
=
∑
n
=
0
∞
l
n
(
n
)
I
(
R
−
I
)
n
n
!
=
∑
n
=
1
∞
l
n
(
n
)
I
(
R
−
I
)
n
n
!
=
∑
n
=
1
∞
(
−
1
)
n
−
1
(
R
−
I
)
n
n
=
∑
n
=
0
∞
(
−
1
)
n
(
R
−
I
)
n
+
1
n
+
1
\begin{aligned} ln(R) & =\sum_{n=0}^\infty\frac{ln^{(n)}I(R-I)^n}{n!} \\ & = \sum_{n=1}^\infty\frac{ln^{(n)}I(R-I)^n}{n!} \\ & = \sum_{n=1}^\infty\frac{(-1)^{n-1}(R-I)^n}{n}\\ & = \sum_{n=0}^\infty\frac{(-1)^{n}(R-I)^{n+1}}{n+1} \end{aligned}
ln(R)=n=0∑∞n!ln(n)I(R−I)n=n=1∑∞n!ln(n)I(R−I)n=n=1∑∞n(−1)n−1(R−I)n=n=0∑∞n+1(−1)n(R−I)n+1