目录
语法
说明
示例
质点-弹簧系统
双体振荡器
ss2tf函数的功能是将状态空间表示形式转换为传递函数。
语法
[b,a] = ss2tf(A,B,C,D)
[b,a] = ss2tf(A,B,C,D,ni)说明
[b,a] = ss2tf(A,B,C,D) 将方程组的状态空间表示形式转换为等同的传递函数。ss2tf 返回连续时间方程组的拉普拉斯变换传递函数和离散时间方程组的 Z 变换传递函数。
[b,a] = ss2tf(A,B,C,D,ni) 返回当具有多个输入的方程组的第 ni 个输入受单位冲激影响时所生成的传递函数。
示例
质点-弹簧系统
一维离散时间震荡系统由单位质点 m 通过一根单位弹性常量弹簧连接到墙壁构成。传感器以 Fs=5 Hz 对质量的加速度 a 取样。
生成 50 个时间样本。定义采样间隔 Δt=1/Fs。
Fs = 5;
dt = 1/Fs;
N = 50;
t = dt*(0:N-1);振荡器可以通过状态空间方程描述。
其中 
是状态向量，r 和 v 分别是质点的位置和速度，而矩阵
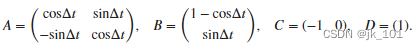
A = [cos(dt) sin(dt);-sin(dt) cos(dt)];
B = [1-cos(dt);sin(dt)];
C = [-1 0];
D = 1;系统使用正方向的单位冲激进行刺激。使用该状态空间模型计算系统从全零的初始状态开始的时间演进。
u = [1 zeros(1,N-1)];
x = [0;0];
for k = 1:N
y(k) = C*x + D*u(k);
x = A*x + B*u(k);
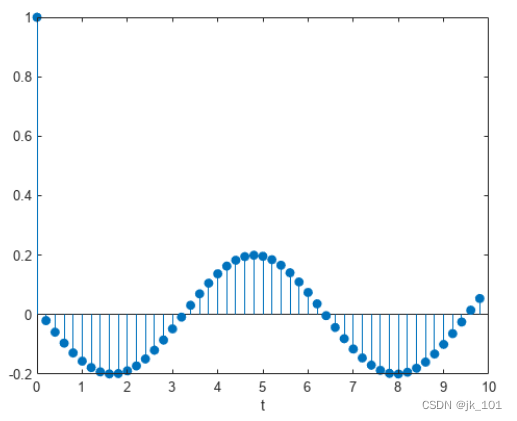
end以时间函数形式绘制质量的加速度。
stem(t,y,'filled')
xlabel('t')如图所示：
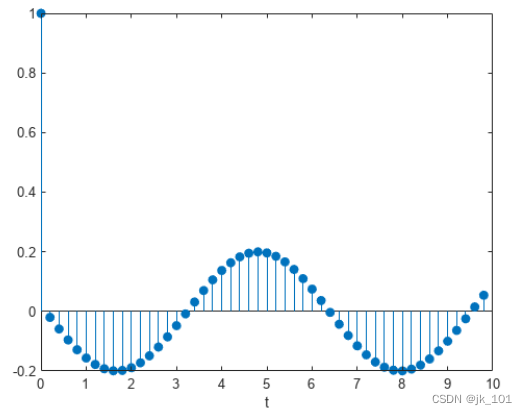
使用传递函数 H(z) 过滤输入以计算时间依赖加速度。绘制结果。
[b,a] = ss2tf(A,B,C,D);
yt = filter(b,a,u);
stem(t,yt,'filled')
xlabel('t')如图所示：
系统的传递函数包含一个解析式：
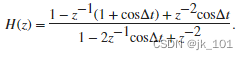
使用表达式过滤输入。绘制响应。
bf = [1 -(1+cos(dt)) cos(dt)];
af = [1 -2*cos(dt) 1];
yf = filter(bf,af,u);
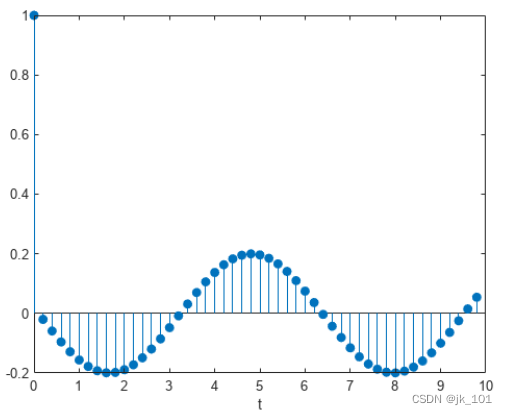
stem(t,yf,'filled')
xlabel('t')如图所示：
所有这三种情况下的结果都相同。
双体振荡器
理想的一维振荡系统由位于两面墙壁间的两个单位质点 m1 和 m2 组成。每个质点通过一根单位弹性常量弹簧连接到最近的墙壁。另外一根弹簧连接这两个质点。传感器以 Fs=16 Hz 的频率对 a1 和 a2（质点的加速度）采样。
将总测量时间指定为 16 秒。定义采样间隔 Δt=1/Fs。
Fs = 16;
dt = 1/Fs;
N = 257;
t = dt*(0:N-1);系统可以由状态空间模型描述
其中
是状态向量，ri 和 vi 分别是第 i 个质点的位置和速度。输入向量 
，输出向量
。状态空间矩阵为
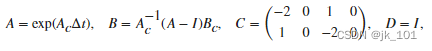
连续时间状态空间矩阵为
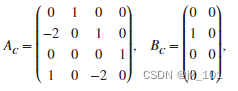
I 表示合适大小的单位矩阵。
Ac = [0 1 0 0; -2 0 1 0; 0 0 0 1; 1 0 -2 0];
A = expm(Ac*dt);
Bc = [0 0; 1 0; 0 0; 0 1];
B = Ac\(A-eye(4))*Bc;
C = [-2 0 1 0; 1 0 -2 0];
D = eye(2);第一个质点 m1 接收正向的单位冲激。
ux = [1 zeros(1,N-1)];
u0 = zeros(1,N);
u = [ux;u0];使用该模型计算系统从全零的初始状态开始的时间演进。
x = [0 0 0 0]';
y = zeros(2,N);
for k = 1:N
y(:,k) = C*x + D*u(:,k);
x = A*x + B*u(:,k);
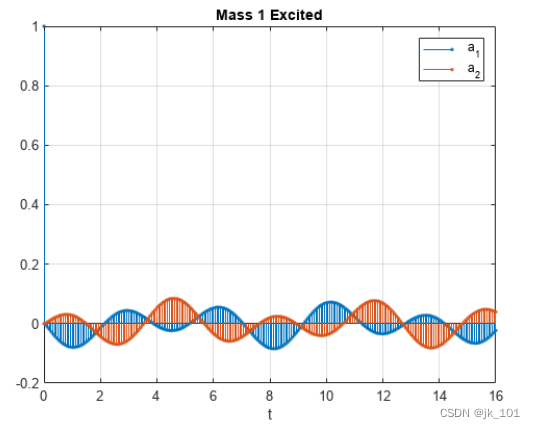
end以时间函数形式绘制两个质点的加速度。
stem(t,y','.')
xlabel('t')
legend('a_1','a_2')
title('Mass 1 Excited')
grid如图所示：
将系统转换为其传递函数表示形式。求得对第一个质点的正单位冲激刺激的系统响应。
[b1,a1] = ss2tf(A,B,C,D,1);
y1u1 = filter(b1(1,:),a1,ux);
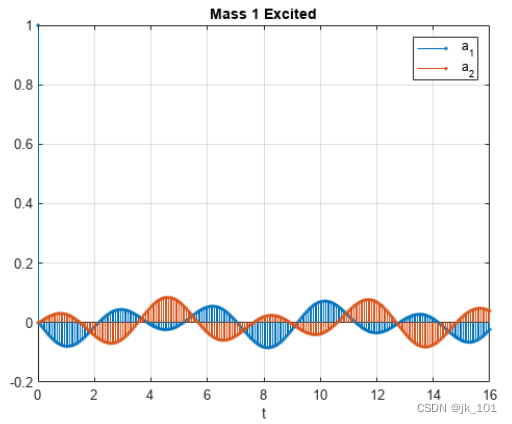
y1u2 = filter(b1(2,:),a1,ux);绘制结果。传递函数提供与状态空间模型相同的响应。
stem(t,[y1u1;y1u2]','.')
xlabel('t')
legend('a_1','a_2')
title('Mass 1 Excited')
grid如图所示：
系统将重置为其初始配置。现在，其他质点 m2 接收正向单位冲激。计算该系统的时间演进。
u = [u0;ux];
x = [0;0;0;0];
for k = 1:N
y(:,k) = C*x + D*u(:,k);
x = A*x + B*u(:,k);
end绘制加速度。将交换各个质点的响应。
stem(t,y','.')
xlabel('t')
legend('a_1','a_2')
title('Mass 2 Excited')
grid如图所示：
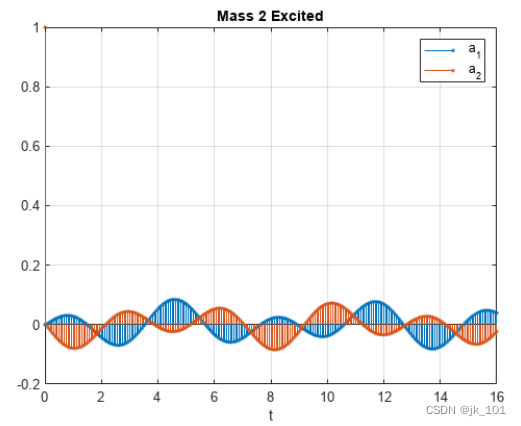
求得对第二个质点的正单位冲激刺激的系统响应。
[b2,a2] = ss2tf(A,B,C,D,2);
y2u1 = filter(b2(1,:),a2,ux);
y2u2 = filter(b2(2,:),a2,ux);绘制结果。传递函数提供与状态空间模型相同的响应。
stem(t,[y2u1;y2u2]','.')
xlabel('t')
legend('a_1','a_2')
title('Mass 2 Excited')
grid如图所示：
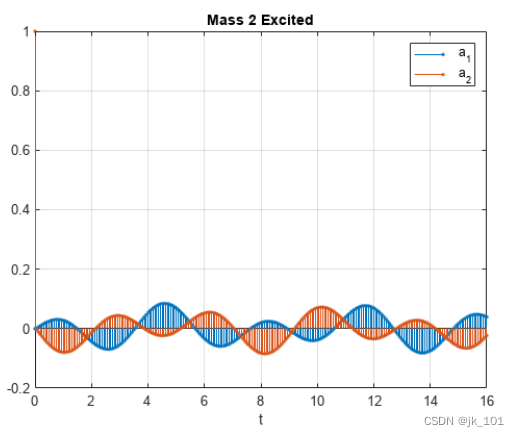
参数说明
A — 状态矩阵
状态矩阵，指定为矩阵。如果方程组具有 p 个输入和 q 个输出并且由 n 个状态变量描述，则 A 为 n×n。
B — 输入-状态矩阵
输入-状态矩阵，指定为矩阵。如果方程组具有 p 个输入和 q 个输出并且由 n 个状态变量描述，则B为 n×p。
C — 状态-输出矩阵
状态-输出矩阵，指定为矩阵。如果方程组具有 p 个输入和 q 个输出并且由 n 个状态变量描述，则C为 q×n。
D — 馈通矩阵
馈通矩阵，指定为矩阵。如果方程组具有 p 个输入和 q 个输出并且由 n 个状态变量描述，则D为 q×p。
ni — 输入索引
输入索引，指定为一个整数标量。如果方程组具有 p 个输入，请使用带尾部参数 ni = 1, …, p 的 ss2tf 计算对应用于第 ni 个输入的单位冲激的响应。
b — 传递函数分子系数
传递函数分子系数，以向量或矩阵的形式返回。如果方程组具有 p 个输入和 q 个输出并且由 n 个状态变量描述，则对于每个输入，b 为 q×(n + 1)。系数按 s 或 z 的幂的降序返回。
a — 传递函数分母系数
传递函数分母系数，以向量的形式返回。如果方程组具有 p 个输入和 q 个输出并且由 n 个状态变量描述，则对于每个输入，a 为 1×(n + 1)。系数按 s 或 z 的幂的降序返回。
传递函数
-
对于离散时间系统，状态空间矩阵通过
与状态向量 x、输入 u 和输出 y 相关。
传递函数是方程组的冲激响应的 Z 变换。可以按状态空间矩阵表示形式将其表示为
-
对于连续时间方程组，状态空间矩阵通过
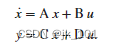
与状态向量 x、输入 u 和输出 y 相关。
传递函数是方程组的冲激响应的拉普拉斯变换。可以按状态空间矩阵表示形式将其表示为
