算法设计过程:
①问题分析
②算法策略
/
建立计算模型
③算法设计与描述
④算法分析
[
算法选择
]
⑤算法实现
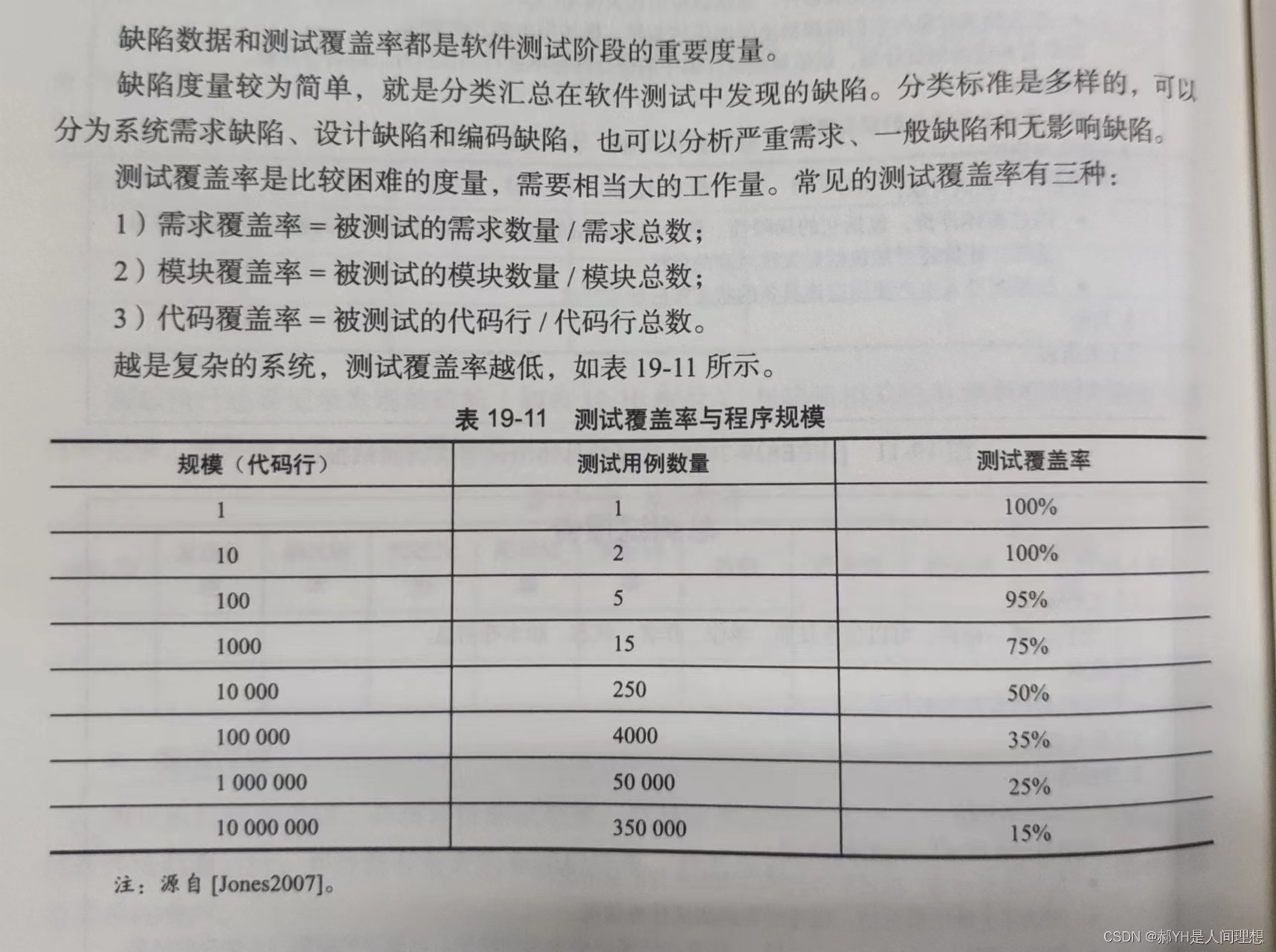
⑥测试与结果分析
⑦文档编制



常用结论:
对数低于多项式;多项式低于指数
常用公式:
定理2.5


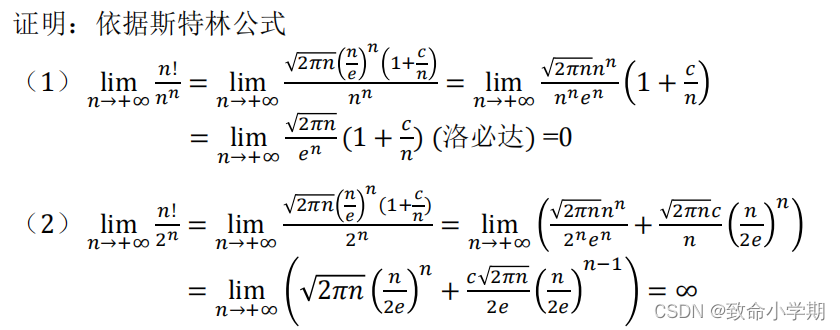
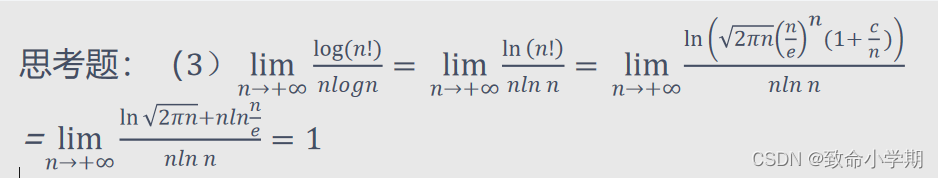




第八章:动态规划
动态规划的基本设计思想
将待求解问题分解成若干个子问题,分阶段求解子问题,
前一阶段子问题的解成为求后续阶段子问题的解的计算信息,
最后用这些子问题的最优解构造出原问题的最优解。
适合用动态规划求解的问题的特征

基本性质:
(1) 子问题重叠性
- ①子问题重复
- ②子问题的解在下一阶段决策中,延续子问题多次使用
(2)最优子结构
- 一个问题的最优解包含着它的子问题的最优解
动态规划算法设计的基本步骤
(1) 找出最优解的性质,并刻画其结构特征。
(2) 按最优解的性质,划分子问题及演算的阶段,递推求解最优解。
(3) 以自底向上或自顶向下的记忆化方法(备忘录法)计算出最优值。
(4) 根据每阶段推算出的局部最优解,构造出全局最优解。