数据结构：二叉树（2）

二叉树的基本操作

获取树的结点总数

遍历思路：

每次遍历一个节点，遍历完nodeSize++，然后遍历它的左右子树

如果遍历到空的节点，就返回0

    public int nodeSize = 0;
    int size(TreeNode root){
        if(root == null){
            return 0;
        }
        nodeSize++;
        size(root.left);
        size(root.right);
        return nodeSize;
    }

子树相加思路

整棵树的节点个数 = 左子树的节点个数+右子树的节点个数 + 根节点

    int size2(TreeNode root){
        if(root == null){
            return 0;
        }
        return size2(root.left) + size2(root.right) + 1;
    }

size2(root.left) 可以理解为左子树所有节点的总数

size2(root.right)可以理解为右子树所有节点的总数

计算二叉树叶结点的总数

遍历思路：遍历结点和左右子树，如果遍历到有一个结点左右子树都为null，那么这个结点就是叶结点，计数器++

    // 获取叶子节点的个数
    //遍历思路
    public int leafNode = 0;
    int getLeafNodeCount(TreeNode root){
        if(root == null){
            return 0;
        }
        if(root.left == null && root.right == null){
            leafNode++;
        }
        getLeafNodeCount(root.left);
        getLeafNodeCount(root.right);
        return leafNode;
    }

子树相加思路：整棵树叶子 = 左子树叶子 + 右子树叶子

    //子树相加思路
    int getLeafNodeCount2(TreeNode root) {
        if (root == null) {
            return 0;
        }
        if (root.left == null && root.right == null) {
            return 1;
        }
        return getLeafNodeCount2(root.left) + getLeafNodeCount2(root.right);
    }

获取第k层的结点个数

思路：

整棵树第k层节点数 = 左子树第k-1层结点数+右子树第k-1层结点数

感觉有杨辉三角的感觉（bushi

    // 获取第K层节点的个数
    public int nodeCount = 0;
    int getKLevelNodeCount(TreeNode root,int k){
        if(root == null){
            return 0;
        }
        if(k == 1){
            return 1;
        }
        return getKLevelNodeCount(root.left,k-1) + getKLevelNodeCount(root.right,k-1);
    }

求二叉树的高度

高度就是最大层数，整棵树的高度 = 左子树的高度和右子树的高度的最大值+1

A的左子树是B，右子树是C

那B的高度怎么求呢？很简单，再递归一下呗，把B当成根结点，左子树B高度就等于B的左子树和右子树高度最大值+1

这样递归递归就能求出左子树总高度了，右子树也同理

    int getHeight(TreeNode root){
        if(root == null){
            return 0;
        }
        int leftHeight = getHeight(root.left);
        int rightHeight = getHeight(root.right);
        
        return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
    }

换种写法

    int getHeight2(TreeNode root){
        if(root == null){
            return 0;
        }

        return getHeight2(root.left) > getHeight2(root.right) 
                ? getHeight2(root.left) + 1 : getHeight2(root.right) + 1;
    }

第二种写法放编译器可以跑，但是放到力扣跑不了

104. 二叉树的最大深度 - 力扣（LeetCode）

它会报这么一个错误

原因就是return的时候好不容易递归完判断左右子树大小，还得再重复递归一次计算总高度，所以跑太久力扣就给你报超时的错误了

检测特定值的元素是否存在

这个直接用前序遍历就行了

    TreeNode find(TreeNode root, int val){
        if(root == null){
            return null;
        }
        //判断根结点是不是
        if(root.val == val){
            return root;
        }
        TreeNode ret = find(root.left, val);
        if(ret != null){
            return ret;//这样就不用去右边了
        }
        TreeNode ret2 = find(root.right,val);
        if(ret2 != null){
            return ret2;
        }
        return null;
    }

二叉树面试题

100. 相同的树 - 力扣（LeetCode）

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

示例 1：

输入：p = [1,2,3], q = [1,2,3]
输出：true

示例 2：

输入：p = [1,2], q = [1,null,2]
输出：false

示例 3：

输入：p = [1,2,1], q = [1,1,2]
输出：false

提示：

两棵树上的节点数目都在范围 [0, 100] 内
-104 <= Node.val <= 104

1.如果两个结点都不为空，就判断值

2.如果一个结点为空一个结点不为空，那必不一样

总结：判断根及其左子树和右子树是否相同

class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        if((p == null && q != null)||(p != null && q == null)){
            return false;
        }
        //上面代码走完后要么两个都为空，要么都不为空
        if(p == null && q == null){
            return true;
        }
        //只剩两个都不为空的情况
        if(p.val != q.val){
            return false;
        }

        return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
    }
}

572. 另一棵树的子树 - 力扣（LeetCode）

给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。

二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

示例 1：

输入：root = [3,4,5,1,2], subRoot = [4,1,2]
输出：true

示例 2：

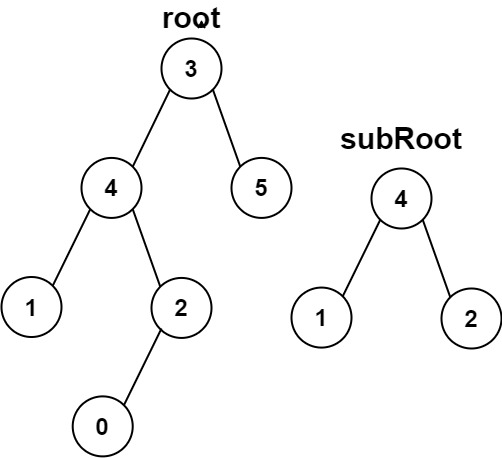
输入：root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
输出：false

提示：

root 树上的节点数量范围是 [1, 2000]
subRoot 树上的节点数量范围是 [1, 1000]
-104 <= root.val <= 104
-104 <= subRoot.val <= 104

1.注意：如果是子树，有可能是两棵相同的树，那可以先比较根结点

2.如果根结点比较完发现不是两棵相同的树，那么subRoot这棵树和root的某一棵子树是相同的

3.判断subRoot和root的左子树是不是相同的，不是就判断右子树。都不是就false了

刚刚那个isSameTree()方法不久能用上了吗

    public boolean isSameTree(TreeNode p, TreeNode q) {
        if((p == null && q != null)||(p != null && q == null)){
            return false;
        }
        //上面代码走完后要么两个都为空，要么都不为空
        if(p == null && q == null){
            return true;
        }
        //只剩两个都不为空的情况
        if(p.val != q.val){
            return false;
        }

        return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
    }
    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        if(isSameTree(root,subRoot)){
            return true;
        }
        if(isSubtree(root.left,subRoot)){
            return true;
        }
        if(isSubtree(root.right,subRoot)){
            return true;
        }
        return false;
    }

欸但是力扣直接给我报了一个空指针异常

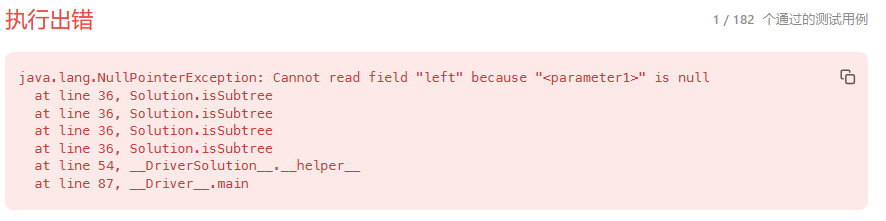
这是因为假如root的左子树就是空的，root第一个if判断完之后进入左子树变成空，空指针进不了第二个if判断，所以跳过直接进入到右子树的if判断，那此时root都为空了，系统自然就报了一个空指针异常了

🆗其实我们在判断根结点是否相同前先判断会不会有空就行了

        if(root == null || subRoot == null){
            return false;
        }

226. 翻转二叉树 - 力扣（LeetCode）

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

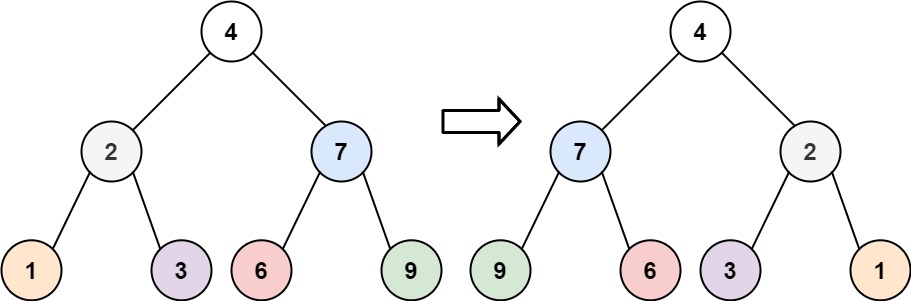
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2：

输入：root = [2,1,3]
输出：[2,3,1]

示例 3：

输入：root = []
输出：[]

提示：

树中节点数目范围在 [0, 100] 内
-100 <= Node.val <= 100

相当于我们进行数组交换一样

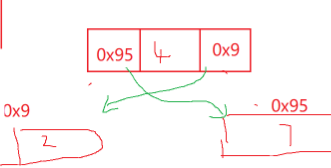
每次遍历到一个结点，就把这个结点的两个引用都换一下就好了

直到所有结点都遍历完成

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if(root == null){
            return null;
        }
        if(root.left == null && root.right == null){
            return root;
        }
        TreeNode tmp = root.left;
        root.left = root.right;
        root.right = tmp;
        //递归搞左右树
        invertTree(root.left);
        invertTree(root.right);
        return root;
    }
}

110. 平衡二叉树 - 力扣（LeetCode）

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

示例 1：

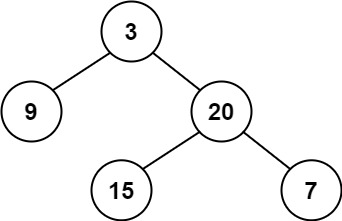
输入：root = [3,9,20,null,null,15,7]
输出：true

示例 2：

输入：root = [1,2,2,3,3,null,null,4,4]
输出：false

示例 3：

输入：root = []
输出：true

提示：

树中的节点数在范围 [0, 5000] 内
-104 <= Node.val <= 104

思路：

1.判断当前根结点的左子树高度-右子树高度的绝对值是否<=1

2.根的左子树是平衡的并且右子树也得是平衡的

这道题高度方法前面已经写完了，直接调用就行（getHeight()）

class Solution {
    public int getHeight(TreeNode root){
        if(root == null){
            return 0;
        }
        int leftHeight = getHeight(root.left);
        int rightHeight = getHeight(root.right);

        return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
    }
    public boolean isBalanced(TreeNode root) {
        if(root == null){
            return true;
        }
        //分别求左右树高度
        int leftHeight = getHeight(root.left);
        int rightHeight = getHeight(root.right);
        //判断绝对差值<=1并且左右子树都平衡
        return Math.abs(leftHeight-rightHeight) <= 1 
        && isBalanced(root.left) && isBalanced(root.right);
    }
}

这里的时间复杂度是O(N^2)，在求左子树和右子树高度调用getHeight时间复杂度已经是O(N)了，return部分再调用isBalance，相当于又遍历了一遍所有的n个结点，isBalance嵌套了getHeight，时间复杂度就是n*n了

进阶难度：使用O(N）的时间复杂度来计算

我们在求子树高度的时候，返回高度时直接让他们进行比较，如果>1就返回-1给根结点

class Solution {
    public int getHeight(TreeNode root){
        if(root == null){
            return 0;
        }
        int leftHeight = getHeight(root.left);
        int rightHeight = getHeight(root.right);

        if(leftHeight >= 0 && rightHeight>=0
        && Math.abs(leftHeight - rightHeight)<=1){
          //返回真实高度
          return Math.max(leftHeight,rightHeight)+1;
        }else{
          return -1;
        }
    }
    public boolean isBalanced(TreeNode root) {
        if(root == null){
            return true;
        }
        int leftHeight = getHeight(root.left);
        int rightHeight = getHeight(root.right);
        return getHeight(root) >= 0;
    }
}

达到O(n)的时间复杂度

101. 对称二叉树 - 力扣（LeetCode）

给你一个二叉树的根节点 root ，检查它是否轴对称。

示例 1：

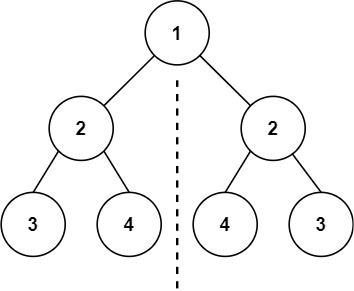
输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

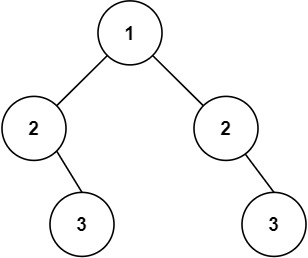
输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

树中节点数目在范围 [1, 1000] 内
-100 <= Node.val <= 100

不对称：

1.一个为空另一个不为空

2.值不一样

3.左树的左和右树的左对称？左树的右和右树的左对称？

注意：left和right都为空就是对称

    public boolean isSymmetric(TreeNode root) {
        if(root == null){
          return true;
        }
        return isSymmetricChild(root.left,root.right);
    }


    private boolean isSymmetricChild(TreeNode leftTree, TreeNode rightTree){
      if((leftTree != null && rightTree == null) || (leftTree == null && rightTree != null)){
        return false;
      }
      if(leftTree == null && rightTree == null){
        return true;
      }
      if(leftTree.val != rightTree.val){
        return false;
      }
      return isSymmetricChild(leftTree.left,rightTree.right) 
      && isSymmetricChild(leftTree.right,rightTree.left);
    }

二叉树遍历_牛客题霸_牛客网 (nowcoder.com)

描述

编一个程序，读入用户输入的一串先序遍历字符串，根据此字符串建立一个二叉树（以指针方式存储）。例如如下的先序遍历字符串： ABC##DE#G##F### 其中“#”表示的是空格，空格字符代表空树。建立起此二叉树以后，再对二叉树进行中序遍历，输出遍历结果。

输入描述：

输入包括1行字符串，长度不超过100。

输出描述：

可能有多组测试数据，对于每组数据，输出将输入字符串建立二叉树后中序遍历的序列，每个字符后面都有一个空格。每个输出结果占一行。

示例1

输入：

abc##de#g##f###

输出：

c b e g d f a

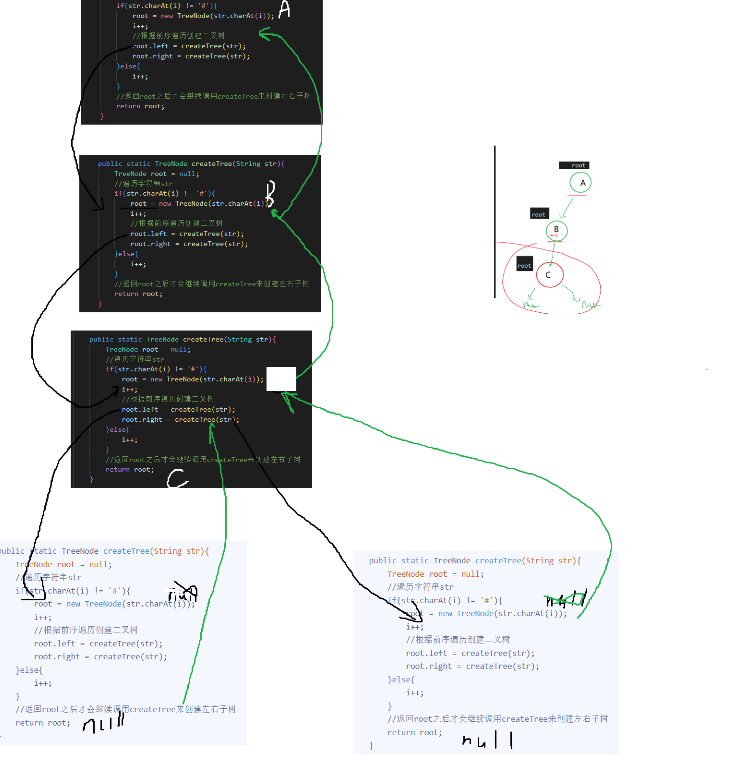
思路：遍历这个字符串，根据前序遍历来创建二叉树，最后再用中序遍历这棵树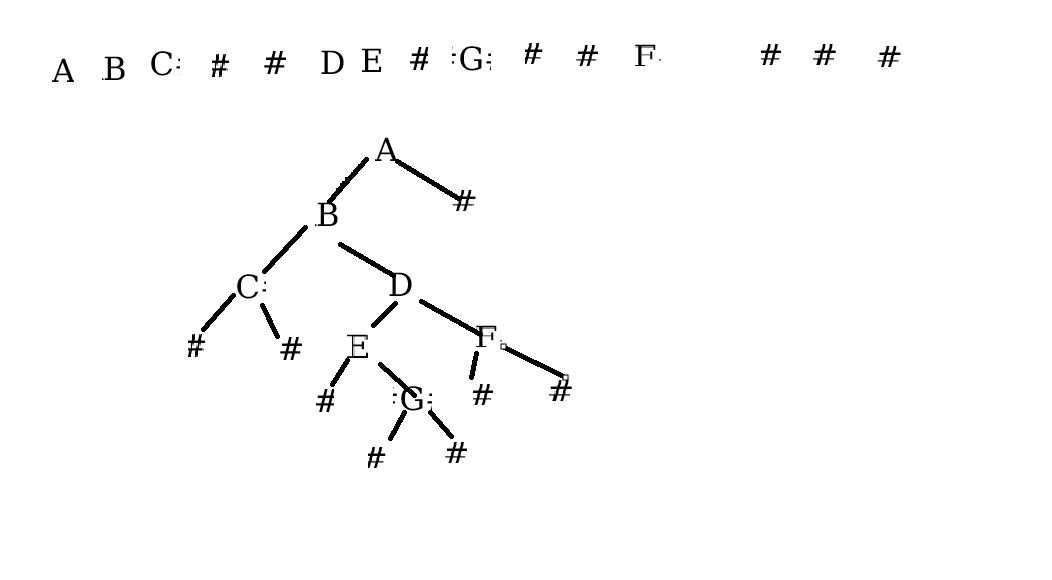

    public static int i = 0;
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        // 注意 hasNext 和 hasNextLine 的区别
        while (in.hasNextLine()) { // 注意 while 处理多个 case
            String str = in.nextLine();
            TreeNode root = createTree(str);
            inorder(root);
        }
    }

    public static TreeNode createTree(String str){
        TreeNode root = null;
        //遍历字符串str
        if(str.charAt(i) != '#'){
            root = new TreeNode(str.charAt(i));
            i++;
            //根据前序遍历创建二叉树
            root.left = createTree(str);
            root.right = createTree(str);
        }else{
            i++;
        }
        //返回root之后才会继续调用createTree来创建左右子树
        return root;
    }

    public static void inorder(TreeNode root){
        if(root == null){
            return ;
        }
        inorder(root.left);
        System.out.print(root.val+" ");
        inorder(root.right);
    }