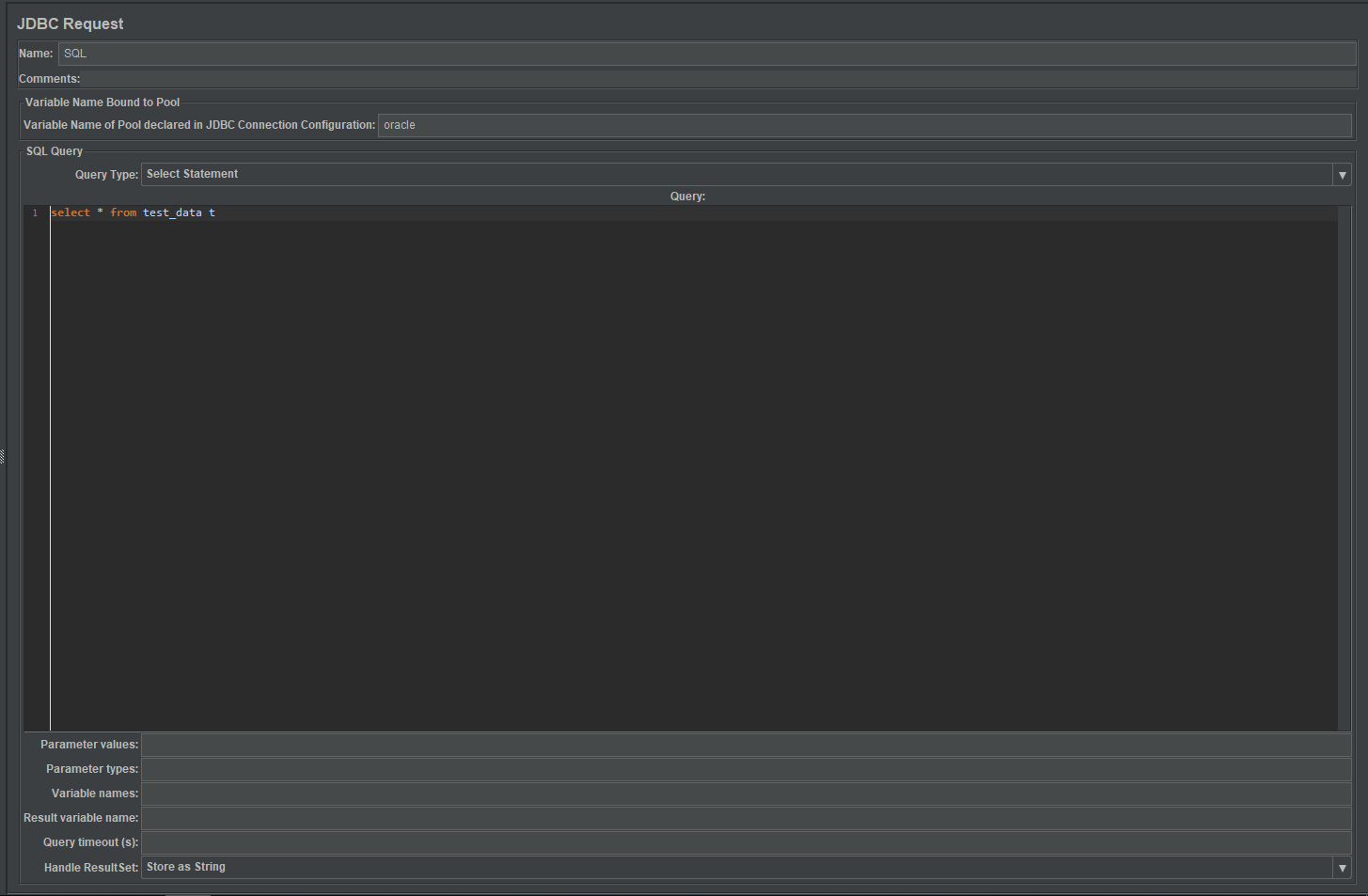
392.判断子序列

    
    let n=s.length
    let a=0
    if(n===0)
     return true 
    for(let i=0;i<t.length;i++){
        if(s[a]===t[i])
            a++
        if(a===n)
        return true
    }
    return false


// s、t的长度
    const [m, n] = [s.length, t.length];
    // dp全初始化为0
    const dp = new Array(m + 1).fill(0).map(x => new Array(n + 1).fill(0));
    for (let i = 1; i <= m; i++) {
        for (let j = 1; j <= n; j++) {
            // 更新dp[i][j]，两种情况
            if (s[i - 1] === t[j - 1]) {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            } else {
                dp[i][j] = dp[i][j - 1];
            }
        }
    }
    // 遍历结束，判断dp右下角的数是否等于s的长度
    return dp[m][n] === m ? true : false;

第一想法

• dp[i][j] 表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度为dp[i][j]。
• if (s[i - 1] == t[j - 1])
  t中找到了一个字符在s中也出现了
  if (s[i - 1] != t[j - 1])
  相当于t要删除元素，继续匹配
  

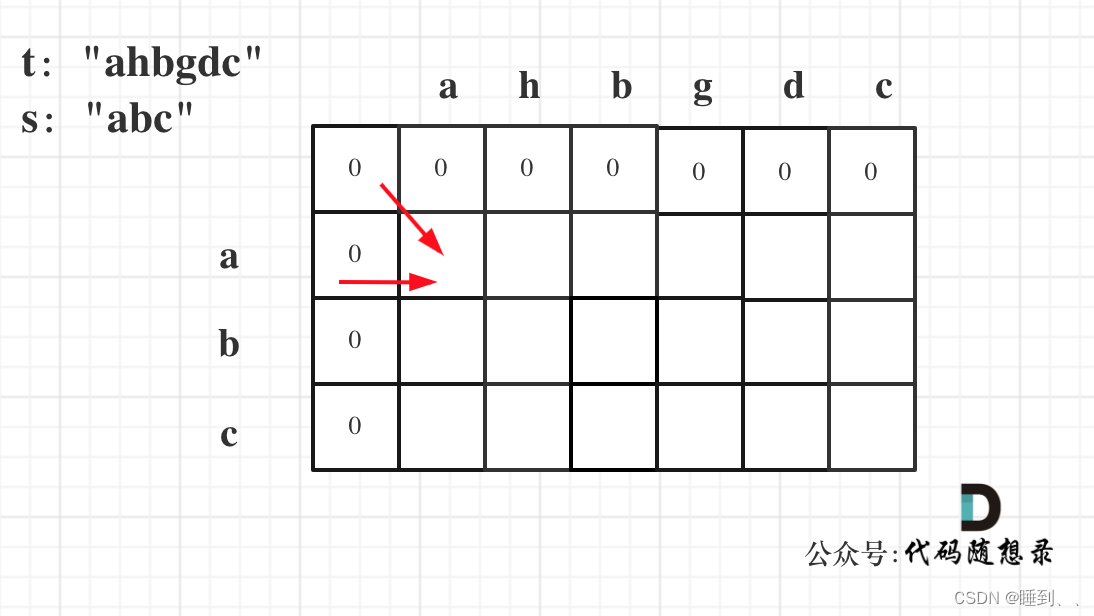
115.不同的子序列

const numDistinct = (s, t) => {
  let dp = Array.from(Array(s.length + 1), () => Array(t.length +1).fill(0));
    for(let i = 0; i <=s.length; i++) {
        dp[i][0] = 1;
    }
    
    for(let i = 1; i <= s.length; i++) {
        for(let j = 1; j<= t.length; j++) {
            if(s[i-1] === t[j-1]) {
                dp[i][j] = dp[i-1][j-1] + dp[i-1][j];
            } else {
                dp[i][j] = dp[i-1][j]
            }
        }
    }
    return dp[s.length][t.length];

};

思想

/**
对于不连续的子串匹配，s为主串，t为匹配串，s=abcd,t=ad时，就算s的b和t的d不匹配也没关系，把s的b、c都删了，那就匹配了！
并且每一个结果都是会叠加直到结束的！如s=aaba,t=a，dp[0][0]=1,dp[1][0]=1+dp[0][0]2,dp[2][0]=dp[1][0]=2,dp[3][0]=1+dp[2][0]=3

    dp:dp的构造类似718. 最长连续重复子数组【但是这里】
    1.定义dp:dp[i][j]：以s[i]为结尾、t[j]为结尾的两个子串满足要求的个数，即t子串存在s子串中的个数
    2.递推公式:
    对于每一次s[i]与t[j]进行匹配，由于本题是不连续的匹配子序列，如例子：s="abcd",t="abd",当nums1[2]!=nums2[2]时，这个时候若是求解连续相同子序列的话，那么dp就要置0了！
    但是这儿求解的是不连续的，所以即便当前元素不匹配也没关系，跳过当前元素s[i]，保留上一个元素s[i-1]与t[j]的匹配结果即dp[i-1][t]，然后后面继续匹配就行了！
    if(s[i]==t[j])
        dp[i][j]=dp[i-1][j-1] + dp[i-1][j]，这个后面的dp[i-1][j]表示删除当前s[i]元素，保留上一个元素s[i-1]与t[j]的匹配结果即dp[i-1][t];如：s=bagg,t=bag,当i=3,j=2时,dp[3][2]=dp[2][1]即0 + dp[3-1][2]即1 = 1 !!! 
        <<<--------即模拟了保留s[i]和删除s[i]的两次过程，保留s[i]则+dp[i-1][j-1]，删除s[i]则+dp[i-1][i]
    else 
        dp[i][j]=dp[i-1][j],若当前s[i]与t[j]不匹配，那么就删除s[i]，保留上一轮的结果即可，如例子:s=abcd,t=ad,dp[0][0]=1,有dp[1][0]=dp[0][0]=1,则dp[2][0]=dp[1][0]=1,dp[3][1]=dp[2][0]=1！
    递推方向:i、j两层循环，从左到右从上到下
    3.初始化:当i=0、t=任意时，s[0]不可能包含t[j]即dp[0][j]=0,当i任意、j=0时,只要s[i]=t[0]，就有机会s包含t，即dp[i][0]=s[i]==t[0]
*/