大家好，我是怒码少年小码。

上一篇讲了二分查找，今天我们看看它的难度扩展。

有序数组转为二叉搜索树

LeetCode 108：给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 高度平衡 二叉搜索树。

高度平衡:二叉树是一棵满足每个节点的左右两个子树的高度差的绝对值不超过1的二叉树。

二叉搜索树的中序遍历就是有序数组，相当于现在知道中序遍历的结果，让你构造二叉树，是不是很简单？答案也有很多种，但是这里限制了左右子树的高度差绝对值不能超过1，答案就少了。

分析：二叉搜索树的根节点的左子树上的结点的值都比根节点的值小，根节点的右子树上的结点的值都比根节点的值大；而根节点的左子树中的根节点也符合这一条件，根节点的右子树中的根节点也符合这一条件。

所以我们可以使用int mid = (left + right) / 2;将数组用中间元素分出左右数组，中间元素作为根节点，再从左右数组中分别找出左右数组中的中间元素当作根节点的左右结点，如此循环往复，知道数组为空。所以这本质上就是一个二分查找。

终止条件：left > right。代码如下：

TreeNode* helper(vector<int> nums, int left, int right) {
	if (left > right) {
		return nullptr;
	}
	
	//总是选择中间位置左边的数字为根节点
	int mid = (left + right) / 2;

	TreeNode* root = new TreeNode(nums[mid]);
	//返回mid左边数组构造的左子树
	root->left = helper(nums, left, mid - 1);
	//返回mid右边数组构造的右子树
	root->right = helper(nums, mid + 1, right);

	return root;
}

TreeNode* sortedArrayToBST(vector<int> nums) {
	return helper(nums, 0, nums.size() - 1);
}

寻找两个正序数组的中位数

LeetCode 4：给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和nums2。请你找出并返回这两个正序数组的中位数 。算法的时间复杂度应该为 O(log (m+n)) 。

• 输入：nums1 = [1,2] nums2 = [3, 4]
• 输出：2.50000
• 解释：合并数组 = [1,2,3,4], 中位数 (2 + 3) / 2 = 2.5

这道题如果没有时间复杂度的限制可以有很多种解决方法：

1. 暴力解题：合并两个数组，然后再遍历找到中位数。
2. 中位数就是 位于(m+n)/2 = k位置上的数，同时遍历两个数组，比较大小，移动指针，找到第k个大的元素。

但是很显然，时间复杂度都不对，想让有log ， 一般都要使用二分、堆和快排的方法。

接下来使用二分的方法讲解：当m+n为奇数，中位数是有序数组的第（m+n)/2个元素；为偶数，中位数是第(m+n)/2个元素和第(m+n)/2 + 1个元素的平均值。所以，这道题转化成寻找两个有序数组的第 k 小的数，k为(m+n)/2或者(m+n)/2 + 1。

假如有两个有序数组nums1和nums2，要找到第k个元素，我们先比较nums1[k/2-1]和nums2[k/2-1]。比较完大小后有以下几种情况：

• 如果nums1[k/2-1] < nums2[k/2-1],则比nums1[k/2-1]小的数最多只有nums1的前k/2 - 1个数和nums2的前k/2 - 1个，因此比其小的数最多只有k-2个，因此nums1[k/2 - 1]不可能是第k个数，那么便可以排除掉nums1[0]到nums1[k/2 - 1]的数，也就是一次砍掉一半。

如下图中第一种情况

• 如果nums1[k/2-1] > nums2[k/2-1],便可以排除掉nums2[0]到nums2[k/2 - 1]的数。

如下图中第二种情况

• 如果nums1[k/2-1] = nums2[k/2-1], 则归入第一种情况处理。

如下图中第三种情况

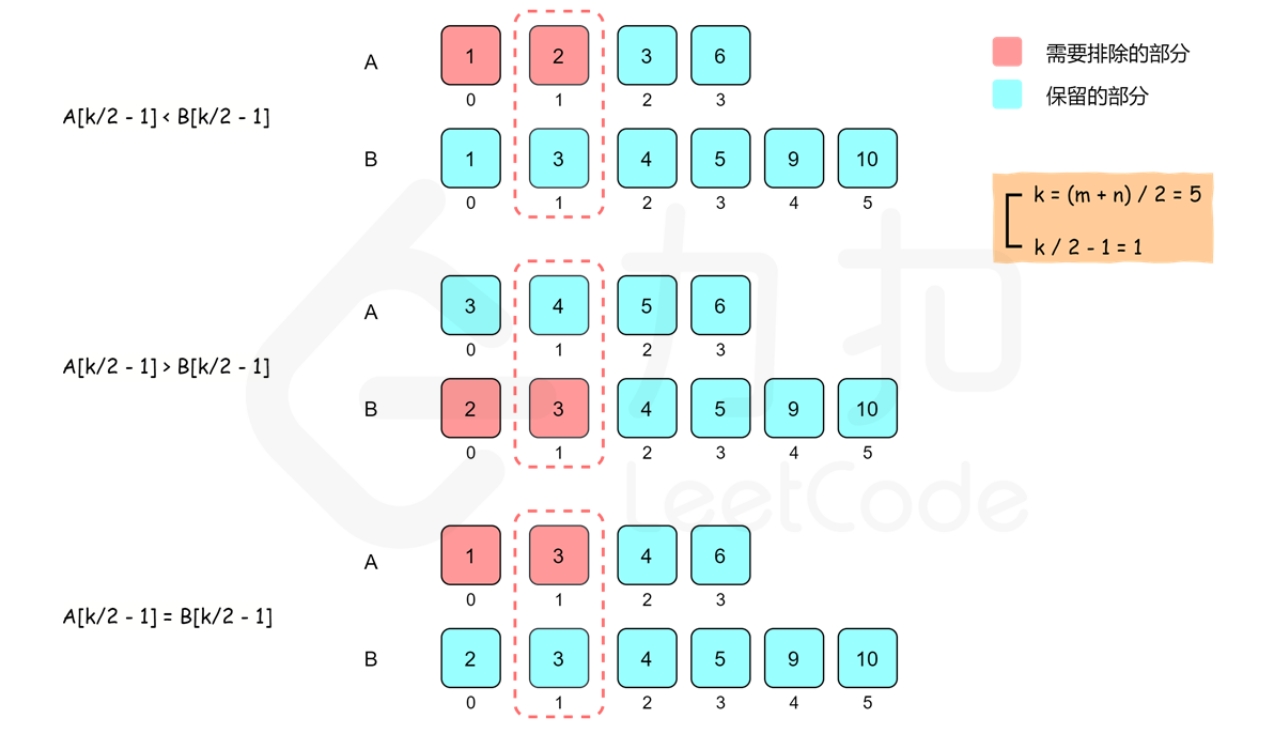
所以我们每次都能缩小一半范围，那最后我们就可以以log的时间复杂度找到我们要的中位数啦！

在此之前，我们还需要处理以下几个特殊情况：

• 如果nums1[k/2 - 1] 或者 nums2[k/2 - 1]越界，那我们我们可以选取其对应数组的最后一个元素。在这种情况下，我们必须根据排除的个数减少k的值，而不能直接将k减去k/2。

• 如果k=1,我们只需要返回两个数组首元素的最小值就可以了。

int getKthElement(const vector<int>& nums1, const vector<int>& nums2, int k) {
    int m = nums1.size();
    int n = nums2.size();
    int index1 = 0, index2 = 0;

    while (true) {
        // 边界情况
        if (index1 == m) {
            return nums2[index2 + k - 1];
        }
        if (index2 == n) {
            return nums1[index1 + k - 1];
        }
        if (k == 1) {
            return min(nums1[index1], nums2[index2]);
        }

        // 正常情况
        int newIndex1 = min(index1 + k / 2 - 1, m - 1);
        int newIndex2 = min(index2 + k / 2 - 1, n - 1);
        int pivot1 = nums1[newIndex1];
        int pivot2 = nums2[newIndex2];
        if (pivot1 <= pivot2) {
            k -= newIndex1 - index1 + 1;
            index1 = newIndex1 + 1;
        }
        else {
            k -= newIndex2 - index2 + 1;
            index2 = newIndex2 + 1;
        }
    }
}

double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
	int totalLength = nums1.size() + nums2.size();
	if (totalLength % 2 == 1) {
		return getKthElement(nums1, nums2, (totalLength + 1) / 2);
	}
	else {
		return (getKthElement(nums1, nums2, totalLength / 2) + getKthElement(nums1, nums2, totalLength / 2 + 1)) / 2.0;
	}
}

本篇参考了这篇文章

END

最后一道题是力扣上的困难题，这么说吧，我觉得我像一个废物😁😁。