C++标准模板（STL）- 类型支持 (数值极限，epsilon，round_error，infinity)

news2025/1/17 15:29:56

数值极限

提供查询所有基础数值类型的性质的接口

定义于头文件 <limits>

template< class T > class numeric_limits;

numeric_limits 类模板提供查询各种算术类型属性的标准化方式（例如 int 类型的最大可能值是 std::numeric_limits<int>::max() ）。
 

返回 1.0 与给定类型的下个可表示值的差

std::numeric_limits<T>::epsilon

static T epsilon() throw();

(C++11 前)

static constexpr T epsilon() noexcept;

(C++11 起)

 返回机器 epsilon ，即 1.0 与浮点类型 T 的下个可表示值的差。它仅若 std::numeric_limits<T>::is_integer == false 才有意义。

返回值

Tstd::numeric_limits<T>::epsilon()
/* non-specialized */T()
boolfalse
char​0​
signed char​0​
unsigned char​0​
wchar_t​0​
char8_t​0​
char16_t​0​
char32_t​0​
short​0​
unsigned short​0​
int​0​
unsigned int​0​
long​0​
unsigned long​0​
long long​0​
unsigned long long​0​
floatFLT_EPSILON
doubleDBL_EPSILON
long doubleLDBL_EPSILON

 调用示例

#include <iostream>
#include <string>
#include <limits>
#include <cstdint>
#include <cfloat>

struct SName
{
};

//偏特化
struct SPartSpec
{
};

namespace std
{
template<>
struct numeric_limits<SPartSpec>
{
    static _GLIBCXX_USE_CONSTEXPR bool is_specialized   = true;
    static _GLIBCXX_USE_CONSTEXPR bool is_signed        = true;
    static _GLIBCXX_USE_CONSTEXPR bool is_integer       = true;
    static _GLIBCXX_USE_CONSTEXPR bool is_exact         = true;
    static _GLIBCXX_USE_CONSTEXPR bool has_infinity     = true;
    static _GLIBCXX_USE_CONSTEXPR bool has_quiet_NaN    = true;
    static _GLIBCXX_USE_CONSTEXPR bool has_signaling_NaN = true;
    static _GLIBCXX_USE_CONSTEXPR float_denorm_style has_denorm     = denorm_present;
    static _GLIBCXX_USE_CONSTEXPR bool has_denorm_loss  = true;
    static _GLIBCXX_USE_CONSTEXPR float_round_style round_style     = round_toward_neg_infinity;
    static _GLIBCXX_USE_CONSTEXPR bool is_iec559        = true;
    static _GLIBCXX_USE_CONSTEXPR bool is_bounded       = true;
    static _GLIBCXX_USE_CONSTEXPR bool is_modulo        = true;
    static _GLIBCXX_USE_CONSTEXPR int  digits           = CHAR_BIT;
    static _GLIBCXX_USE_CONSTEXPR int  digits10         = CHAR_BIT;
    static _GLIBCXX_USE_CONSTEXPR int  max_digits10     = DECIMAL_DIG;
    static _GLIBCXX_USE_CONSTEXPR int  radix            = FLT_RADIX;
    static _GLIBCXX_USE_CONSTEXPR int  min_exponent     = FLT_MIN_EXP;
    static _GLIBCXX_USE_CONSTEXPR int  min_exponent10   = FLT_MIN_10_EXP;
    static _GLIBCXX_USE_CONSTEXPR int  max_exponent     = FLT_MAX_EXP;
    static _GLIBCXX_USE_CONSTEXPR int  max_exponent10   = FLT_MAX_EXP;
    static _GLIBCXX_USE_CONSTEXPR bool traps            = true;
    static _GLIBCXX_USE_CONSTEXPR bool tinyness_before  = true;

    static _GLIBCXX_CONSTEXPR int
    min() _GLIBCXX_USE_NOEXCEPT { return  CHAR_MIN ; }
    static _GLIBCXX_CONSTEXPR int
    lowest() _GLIBCXX_USE_NOEXCEPT { return  CHAR_MIN ; }
    static _GLIBCXX_CONSTEXPR int
    max() _GLIBCXX_USE_NOEXCEPT { return  CHAR_MAX ; }
    static _GLIBCXX_CONSTEXPR int
    epsilon() _GLIBCXX_USE_NOEXCEPT { return  LDBL_EPSILON ; }
};
}

int main()
{
    std::cout << std::boolalpha;
    std::cout << "std::numeric_limits<bool>::epsilon():                 "
              << std::numeric_limits<bool>::epsilon() << std::endl;
    std::cout << "std::numeric_limits<char>::epsilon():                 "
              << std::numeric_limits<char>::epsilon() << std::endl;
    std::cout << "std::numeric_limits<signed char>::epsilon():          "
              << std::numeric_limits<signed char>::epsilon() << std::endl;
    std::cout << "std::numeric_limits<unsigned char>::epsilon():        "
              << std::numeric_limits<unsigned char>::epsilon() << std::endl;
    std::cout << "std::numeric_limits<wchar_t>::epsilon():              "
              << std::numeric_limits<wchar_t>::epsilon() << std::endl;
    std::cout << "std::numeric_limits<char16_t>::epsilon():             "
              << std::numeric_limits<char16_t>::epsilon() << std::endl;
    std::cout << "std::numeric_limits<char32_t>::epsilon():             "
              << std::numeric_limits<char32_t>::epsilon() << std::endl;
    std::cout << "std::numeric_limits<short>::epsilon():                "
              << std::numeric_limits<short>::epsilon() << std::endl;
    std::cout << "std::numeric_limits<unsigned short>::epsilon():       "
              << std::numeric_limits<unsigned short>::epsilon() << std::endl;
    std::cout << "std::numeric_limits<int>::epsilon():                  "
              << std::numeric_limits<int>::epsilon() << std::endl;
    std::cout << "std::numeric_limits<unsigned int>::epsilon():         "
              << std::numeric_limits<unsigned int>::epsilon() << std::endl;
    std::cout << "std::numeric_limits<long>::epsilon():                 "
              << std::numeric_limits<long>::epsilon() << std::endl;
    std::cout << "std::numeric_limits<unsigned long>::epsilon():        "
              << std::numeric_limits<unsigned long>::epsilon() << std::endl;
    std::cout << "std::numeric_limits<long long>::epsilon():            "
              << std::numeric_limits<long long>::epsilon() << std::endl;
    std::cout << "std::numeric_limits<unsigned long long>::epsilon():   "
              << std::numeric_limits<unsigned long long>::epsilon() << std::endl;
    std::cout << "std::numeric_limits<float>::epsilon():                "
              << std::numeric_limits<float>::epsilon() << std::endl;
    std::cout << "std::numeric_limits<double>::epsilon():               "
              << std::numeric_limits<double>::epsilon() << std::endl;
    std::cout << "std::numeric_limits<long double>::epsilon():          "
              << std::numeric_limits<long double>::epsilon() << std::endl;
    std::cout << "std::numeric_limits<std::string>::epsilon():          "
              << std::numeric_limits<std::string>::epsilon() << std::endl;
    //必须偏特化
//    std::cout << "std::numeric_limits<SName>::epsilon():                "
//              << std::numeric_limits<SName>::epsilon() << std::endl;
    std::cout << "std::numeric_limits<SPartSpec>::epsilon():            "
              << std::numeric_limits<SPartSpec>::epsilon() << std::endl;
    return 0;
}

输出

返回给定浮点类型的最大舍入误差

std::numeric_limits<T>::round_error

static T round_error() throw();

(C++11 前)

static constexpr T round_error() noexcept;

(C++11 起)

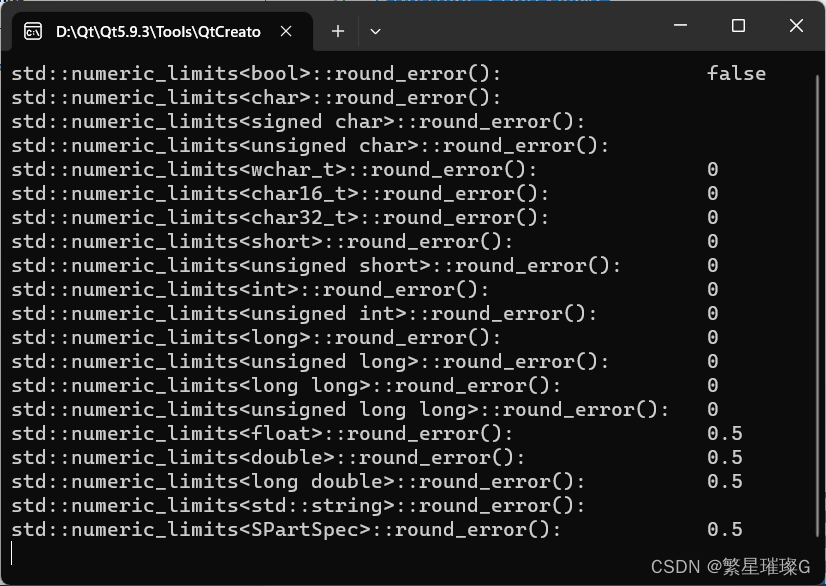
 返回以 ULP （最后位置单位）表示的最大可能舍入错误，其为 ISO 10967 定义，可以从 0.5 （舍入到最近位）变化到 1.0 （舍入到零或无穷大）。它仅若 std::numeric_limits<T>::is_integer == false 才有意义。

返回值

Tstd::numeric_limits<T>::round_error()
/* non-specialized */T()
boolfalse
char​0​
signed char​0​
unsigned char​0​
wchar_t​0​
char8_t​0​
char16_t​0​
char32_t​0​
short​0​
unsigned short​0​
int​0​
unsigned int​0​
long​0​
unsigned long​0​
long long​0​
unsigned long long​0​
float0.5F
double0.5
long double0.5L

调用示例

#include <iostream>
#include <string>
#include <limits>
#include <cstdint>
#include <cfloat>

struct SName
{
};

//偏特化
struct SPartSpec
{
};

namespace std
{
template<>
struct numeric_limits<SPartSpec>
{
    static _GLIBCXX_USE_CONSTEXPR bool is_specialized   = true;
    static _GLIBCXX_USE_CONSTEXPR bool is_signed        = true;
    static _GLIBCXX_USE_CONSTEXPR bool is_integer       = true;
    static _GLIBCXX_USE_CONSTEXPR bool is_exact         = true;
    static _GLIBCXX_USE_CONSTEXPR bool has_infinity     = true;
    static _GLIBCXX_USE_CONSTEXPR bool has_quiet_NaN    = true;
    static _GLIBCXX_USE_CONSTEXPR bool has_signaling_NaN = true;
    static _GLIBCXX_USE_CONSTEXPR float_denorm_style has_denorm     = denorm_present;
    static _GLIBCXX_USE_CONSTEXPR bool has_denorm_loss  = true;
    static _GLIBCXX_USE_CONSTEXPR float_round_style round_style     = round_toward_neg_infinity;
    static _GLIBCXX_USE_CONSTEXPR bool is_iec559        = true;
    static _GLIBCXX_USE_CONSTEXPR bool is_bounded       = true;
    static _GLIBCXX_USE_CONSTEXPR bool is_modulo        = true;
    static _GLIBCXX_USE_CONSTEXPR int  digits           = CHAR_BIT;
    static _GLIBCXX_USE_CONSTEXPR int  digits10         = CHAR_BIT;
    static _GLIBCXX_USE_CONSTEXPR int  max_digits10     = DECIMAL_DIG;
    static _GLIBCXX_USE_CONSTEXPR int  radix            = FLT_RADIX;
    static _GLIBCXX_USE_CONSTEXPR int  min_exponent     = FLT_MIN_EXP;
    static _GLIBCXX_USE_CONSTEXPR int  min_exponent10   = FLT_MIN_10_EXP;
    static _GLIBCXX_USE_CONSTEXPR int  max_exponent     = FLT_MAX_EXP;
    static _GLIBCXX_USE_CONSTEXPR int  max_exponent10   = FLT_MAX_EXP;
    static _GLIBCXX_USE_CONSTEXPR bool traps            = true;
    static _GLIBCXX_USE_CONSTEXPR bool tinyness_before  = true;

    static _GLIBCXX_CONSTEXPR int
    min() _GLIBCXX_USE_NOEXCEPT { return  CHAR_MIN ; }
    static _GLIBCXX_CONSTEXPR int
    lowest() _GLIBCXX_USE_NOEXCEPT { return  CHAR_MIN ; }
    static _GLIBCXX_CONSTEXPR int
    max() _GLIBCXX_USE_NOEXCEPT { return  CHAR_MAX ; }
    static _GLIBCXX_CONSTEXPR int
    epsilon() _GLIBCXX_USE_NOEXCEPT { return  LDBL_EPSILON ; }
    static _GLIBCXX_CONSTEXPR double
    round_error() _GLIBCXX_USE_NOEXCEPT { return  0.5F ; }
};
}

int main()
{
    std::cout << std::boolalpha;
    std::cout << "std::numeric_limits<bool>::round_error():                 "
              << std::numeric_limits<bool>::round_error() << std::endl;
    std::cout << "std::numeric_limits<char>::round_error():                 "
              << std::numeric_limits<char>::round_error() << std::endl;
    std::cout << "std::numeric_limits<signed char>::round_error():          "
              << std::numeric_limits<signed char>::round_error() << std::endl;
    std::cout << "std::numeric_limits<unsigned char>::round_error():        "
              << std::numeric_limits<unsigned char>::round_error() << std::endl;
    std::cout << "std::numeric_limits<wchar_t>::round_error():              "
              << std::numeric_limits<wchar_t>::round_error() << std::endl;
    std::cout << "std::numeric_limits<char16_t>::round_error():             "
              << std::numeric_limits<char16_t>::round_error() << std::endl;
    std::cout << "std::numeric_limits<char32_t>::round_error():             "
              << std::numeric_limits<char32_t>::round_error() << std::endl;
    std::cout << "std::numeric_limits<short>::round_error():                "
              << std::numeric_limits<short>::round_error() << std::endl;
    std::cout << "std::numeric_limits<unsigned short>::round_error():       "
              << std::numeric_limits<unsigned short>::round_error() << std::endl;
    std::cout << "std::numeric_limits<int>::round_error():                  "
              << std::numeric_limits<int>::round_error() << std::endl;
    std::cout << "std::numeric_limits<unsigned int>::round_error():         "
              << std::numeric_limits<unsigned int>::round_error() << std::endl;
    std::cout << "std::numeric_limits<long>::round_error():                 "
              << std::numeric_limits<long>::round_error() << std::endl;
    std::cout << "std::numeric_limits<unsigned long>::round_error():        "
              << std::numeric_limits<unsigned long>::round_error() << std::endl;
    std::cout << "std::numeric_limits<long long>::round_error():            "
              << std::numeric_limits<long long>::round_error() << std::endl;
    std::cout << "std::numeric_limits<unsigned long long>::round_error():   "
              << std::numeric_limits<unsigned long long>::round_error() << std::endl;
    std::cout << "std::numeric_limits<float>::round_error():                "
              << std::numeric_limits<float>::round_error() << std::endl;
    std::cout << "std::numeric_limits<double>::round_error():               "
              << std::numeric_limits<double>::round_error() << std::endl;
    std::cout << "std::numeric_limits<long double>::round_error():          "
              << std::numeric_limits<long double>::round_error() << std::endl;
    std::cout << "std::numeric_limits<std::string>::round_error():          "
              << std::numeric_limits<std::string>::round_error() << std::endl;
    //必须偏特化
//    std::cout << "std::numeric_limits<SName>::round_error():                "
//              << std::numeric_limits<SName>::round_error() << std::endl;
    std::cout << "std::numeric_limits<SPartSpec>::round_error():            "
              << std::numeric_limits<SPartSpec>::round_error() << std::endl;
    return 0;
}

输出

返回给定类型的正无穷大值

std::numeric_limits<T>::infinity

static T infinity() throw();

(C++11 前)

static constexpr T infinity() noexcept;

(C++11 起)

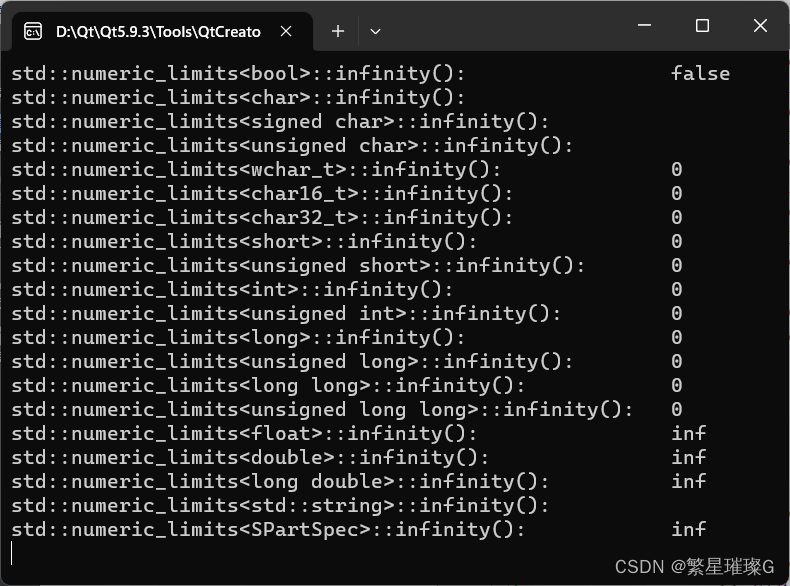
 返回浮点类型 T 所表示的特殊值“正无穷大”。仅若 std::numeric_limits<T>::has_infinity == true 才有意义。在最常见的浮点数二进制表示 IEEE 754 中，正无穷大是所有指数位为 1 而所有尾数位为 0 的值。

返回值

Tstd::numeric_limits<T>::infinity()
/* non-specialized */T()
boolfalse
char​0​
signed char​0​
unsigned char​0​
wchar_t​0​
char8_t​0​
char16_t​0​
char32_t​0​
short​0​
unsigned short​0​
int​0​
unsigned int​0​
long​0​
unsigned long​0​
long long​0​
unsigned long long​0​
floatHUGE_VALF
doubleHUGE_VAL
long doubleHUGE_VALL

调用示例

#include <iostream>
#include <string>
#include <limits>
#include <cstdint>
#include <cfloat>
#include <cmath>

struct SName
{
};

//偏特化
struct SPartSpec
{
};

namespace std
{
template<>
struct numeric_limits<SPartSpec>
{
    static _GLIBCXX_USE_CONSTEXPR bool is_specialized   = true;
    static _GLIBCXX_USE_CONSTEXPR bool is_signed        = true;
    static _GLIBCXX_USE_CONSTEXPR bool is_integer       = true;
    static _GLIBCXX_USE_CONSTEXPR bool is_exact         = true;
    static _GLIBCXX_USE_CONSTEXPR bool has_infinity     = true;
    static _GLIBCXX_USE_CONSTEXPR bool has_quiet_NaN    = true;
    static _GLIBCXX_USE_CONSTEXPR bool has_signaling_NaN = true;
    static _GLIBCXX_USE_CONSTEXPR float_denorm_style has_denorm     = denorm_present;
    static _GLIBCXX_USE_CONSTEXPR bool has_denorm_loss  = true;
    static _GLIBCXX_USE_CONSTEXPR float_round_style round_style     = round_toward_neg_infinity;
    static _GLIBCXX_USE_CONSTEXPR bool is_iec559        = true;
    static _GLIBCXX_USE_CONSTEXPR bool is_bounded       = true;
    static _GLIBCXX_USE_CONSTEXPR bool is_modulo        = true;
    static _GLIBCXX_USE_CONSTEXPR int  digits           = CHAR_BIT;
    static _GLIBCXX_USE_CONSTEXPR int  digits10         = CHAR_BIT;
    static _GLIBCXX_USE_CONSTEXPR int  max_digits10     = DECIMAL_DIG;
    static _GLIBCXX_USE_CONSTEXPR int  radix            = FLT_RADIX;
    static _GLIBCXX_USE_CONSTEXPR int  min_exponent     = FLT_MIN_EXP;
    static _GLIBCXX_USE_CONSTEXPR int  min_exponent10   = FLT_MIN_10_EXP;
    static _GLIBCXX_USE_CONSTEXPR int  max_exponent     = FLT_MAX_EXP;
    static _GLIBCXX_USE_CONSTEXPR int  max_exponent10   = FLT_MAX_EXP;
    static _GLIBCXX_USE_CONSTEXPR bool traps            = true;
    static _GLIBCXX_USE_CONSTEXPR bool tinyness_before  = true;

    static _GLIBCXX_CONSTEXPR int
    min() _GLIBCXX_USE_NOEXCEPT { return  CHAR_MIN ; }
    static _GLIBCXX_CONSTEXPR int
    lowest() _GLIBCXX_USE_NOEXCEPT { return  CHAR_MIN ; }
    static _GLIBCXX_CONSTEXPR int
    max() _GLIBCXX_USE_NOEXCEPT { return  CHAR_MAX ; }
    static _GLIBCXX_CONSTEXPR int
    epsilon() _GLIBCXX_USE_NOEXCEPT { return  LDBL_EPSILON ; }
    static _GLIBCXX_CONSTEXPR double
    round_error() _GLIBCXX_USE_NOEXCEPT { return  0.5F ; }
    static _GLIBCXX_CONSTEXPR double
    infinity() _GLIBCXX_USE_NOEXCEPT { return  HUGE_VAL ; }
};
}

int main()
{
    std::cout << std::boolalpha;
    std::cout << "std::numeric_limits<bool>::infinity():                 "
              << std::numeric_limits<bool>::infinity() << std::endl;
    std::cout << "std::numeric_limits<char>::infinity():                 "
              << std::numeric_limits<char>::infinity() << std::endl;
    std::cout << "std::numeric_limits<signed char>::infinity():          "
              << std::numeric_limits<signed char>::infinity() << std::endl;
    std::cout << "std::numeric_limits<unsigned char>::infinity():        "
              << std::numeric_limits<unsigned char>::infinity() << std::endl;
    std::cout << "std::numeric_limits<wchar_t>::infinity():              "
              << std::numeric_limits<wchar_t>::infinity() << std::endl;
    std::cout << "std::numeric_limits<char16_t>::infinity():             "
              << std::numeric_limits<char16_t>::infinity() << std::endl;
    std::cout << "std::numeric_limits<char32_t>::infinity():             "
              << std::numeric_limits<char32_t>::infinity() << std::endl;
    std::cout << "std::numeric_limits<short>::infinity():                "
              << std::numeric_limits<short>::infinity() << std::endl;
    std::cout << "std::numeric_limits<unsigned short>::infinity():       "
              << std::numeric_limits<unsigned short>::infinity() << std::endl;
    std::cout << "std::numeric_limits<int>::infinity():                  "
              << std::numeric_limits<int>::infinity() << std::endl;
    std::cout << "std::numeric_limits<unsigned int>::infinity():         "
              << std::numeric_limits<unsigned int>::infinity() << std::endl;
    std::cout << "std::numeric_limits<long>::infinity():                 "
              << std::numeric_limits<long>::infinity() << std::endl;
    std::cout << "std::numeric_limits<unsigned long>::infinity():        "
              << std::numeric_limits<unsigned long>::infinity() << std::endl;
    std::cout << "std::numeric_limits<long long>::infinity():            "
              << std::numeric_limits<long long>::infinity() << std::endl;
    std::cout << "std::numeric_limits<unsigned long long>::infinity():   "
              << std::numeric_limits<unsigned long long>::infinity() << std::endl;
    std::cout << "std::numeric_limits<float>::infinity():                "
              << std::numeric_limits<float>::infinity() << std::endl;
    std::cout << "std::numeric_limits<double>::infinity():               "
              << std::numeric_limits<double>::infinity() << std::endl;
    std::cout << "std::numeric_limits<long double>::infinity():          "
              << std::numeric_limits<long double>::infinity() << std::endl;
    std::cout << "std::numeric_limits<std::string>::infinity():          "
              << std::numeric_limits<std::string>::infinity() << std::endl;
    //必须偏特化
//    std::cout << "std::numeric_limits<SName>::infinity():                "
//              << std::numeric_limits<SName>::infinity() << std::endl;
    std::cout << "std::numeric_limits<SPartSpec>::infinity():            "
              << std::numeric_limits<SPartSpec>::infinity() << std::endl;
    return 0;
}

输出

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1104296.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Android查看签名信息系列 · 使用Android Studio获取签名

Android查看签名信息系列 · 使用Android Studio获取签名

前言 Android查看签名信息系列 之使用Android Studio获取签名&#xff0c;通过Android Studio自带的gradle来获取签名信息。 优点&#xff1a;此法可查看 MD5、SHA1 等信息。 缺点&#xff1a;升级某个Studio版本后&#xff0c;没有签名任务了&#xff0c;特别不方便。 实现…
阅读更多...
简单的对称加密

简单的对称加密

异或 异或算法的好处便是数A和数B异或后&#xff0c;把结果再和数A异或便可得到B&#xff0c;或者和数B异或可重新得到数据A。利用异或的这个特性可简单实现数据的加密和解密算法。 恺撒密码 恺撒密码的替换方法是通过排列明文和密文字母表&#xff0c;密文字母表示通过将明…
阅读更多...
【C++11】智能指针的使用以及模拟实现（shared_ptr，unique_ptr，auto_ptr，weak_ptr）

【C++11】智能指针的使用以及模拟实现（shared_ptr，unique_ptr，auto_ptr，weak_ptr）

&#x1f30f;博客主页&#xff1a; 主页 &#x1f516;系列专栏&#xff1a; C ❤️感谢大家点赞&#x1f44d;收藏⭐评论✍️ &#x1f60d;期待与大家一起进步&#xff01; 文章目录 一、 RAII概念一、auto_ptr1.基本使用2.模拟实现 二、unique_ptr1.基本使用2.模拟实现…
阅读更多...
如何禁止在堆上和栈上创建对象

如何禁止在堆上和栈上创建对象

背景 首先需要知道的是&#xff1a; 在栈新建一个对象&#xff0c;不需要调用operator new&#xff0c;创建栈对象时会移动栈顶指针以“挪出”适当大小的空间&#xff0c;然后在这个空间上直接调用对应的构造函数以形成一个栈对象。当对象在栈上创建时&#xff0c;虽然编译器…
阅读更多...
Apache Dubbo的主要项目模块

Apache Dubbo的主要项目模块

Apache Dubbo的项目结构或者主要项目模块如下所示&#xff1a;
阅读更多...
Web架构安全分析/http/URL/Cookie攻击

Web架构安全分析/http/URL/Cookie攻击

Web 架构安全分析 Web 工作机制及基本概念 传统 Web 架构 LAMP 网页 概念 网页就是我们可以通过浏览器上网看到的精美页面&#xff0c;一般都是经过浏览器渲染过的 .html 页面&#xff0c;html 语言在浏览器中渲染。其中包含了CSS、JavaScript 等前端技术。通过浏览器访问…
阅读更多...
excel 日期与时间戳的相互转换

excel 日期与时间戳的相互转换

1、日期转时间戳&#xff1a;B1INT((A1-70*365-19)*86400-8*3600)*1000 2、时间戳转日期&#xff1a;A1TEXT((B1/10008*3600)/8640070*36519,"yyyy-mm-dd hh:mm:ss") 以上为精确到毫秒&#xff0c;只精确到秒不需要乘或除1000。 使用以上方法可以进行excel中日期…
阅读更多...
07AC91 GJR5252300R0101 什么是机器人技术

07AC91 GJR5252300R0101 什么是机器人技术

07AC91 GJR5252300R0101 什么是机器人技术 什么是机器人技术&#xff1f; 机器人学是工程学的一个分支&#xff0c;研究机器人的概念、设计、构造、操作、应用和使用。再深入一点&#xff0c;我们看到机器人被定义为自动操作的机器&#xff0c;它独立地执行一系列动作&#x…
阅读更多...
[计算机提升] 系统及用户操作

[计算机提升] 系统及用户操作

1.4 系统及用户操作 1.4.1 系统操作 1.4.1.1 开机、关机、重启 在Windows系统中&#xff0c;开机&#xff08;Power On&#xff09;&#xff0c;关机&#xff08;Shutdown&#xff09;和重启&#xff08;Restart&#xff09;是指计算机的不同电源控制操作。 开机&#xff1a;…
阅读更多...
官媒代运营：2023年企业如何建立一个成功的品牌？

官媒代运营：2023年企业如何建立一个成功的品牌？

在这个数字化急速发展的时代&#xff0c;企业的成功已不再只依赖于产品质量、资本实力和市场声誉&#xff0c;还在于如何经营营销&#xff0c;以确保品牌能在竞争激烈的市场中脱颖而出。随着时间的推移&#xff0c;营销策略也在不断演变&#xff0c;因此&#xff0c;紧跟潮流变…
阅读更多...
dvaJs在react 项目中的简单使用

dvaJs在react 项目中的简单使用

官网&#xff1a;入门课 | DvaJS 备注&#xff1a;个人学习 代码示例&#xff1a; getColumns.js const getColumns [{title: 姓名, // 列标题dataIndex: name, // 数据字段名称&#xff0c;与数据中的字段名对应key: name, // 列的唯一键},{title: 年龄, // 列标题dataIn…
阅读更多...
Ps：变形

Ps：变形

Ps菜单&#xff1a;编辑/变换/变形 Edit/Transform/Warp 变形 Warp是自由变换的一种模式&#xff0c;不仅可以用于物体的伸缩扭曲&#xff0c;也可用于人体的局部塑形。 除了从菜单打开&#xff0c;通常情况下&#xff0c;按 Ctrl T 进入自由变换&#xff0c;然后在画面上右击…
阅读更多...
stm32 cubeide 闪退 显示self upgrade failed

stm32 cubeide 闪退 显示self upgrade failed

更新或安装新版cubeide时&#xff0c;可能会出现打开后一段时间直接闪退&#xff0c;显示如下图。此时怎么折腾cubeide都是没用的。应该去升级stm32 cubemx。记得打开cubemx时选择用管理员身份打开&#xff0c;升级完成后重新开打。然后尝试打开cubdeide&#xff0c;如果继续报…
阅读更多...
钢铁异常分类140篇Trans 学习笔记 小陈读paper

钢铁异常分类140篇Trans 学习笔记 小陈读paper

钢铁异常分类 对比学习 比较好用 1.首先&#xff0c;为每个实例生成一对样本&#xff0c; 来自同一实例的样本被认为是正例&#xff0c; 来自不同实例的样本被认为是负例。 2.其次&#xff0c;这些样本被馈送到编码器以获得嵌入。 3.在对比损失[16]的影响下&#xff0c; …
阅读更多...
一文了解 Amazon DataZone 使用指南

一文了解 Amazon DataZone 使用指南

Amazon DataZone 现已正式发布。作为一项新的数据管理服务&#xff0c;它能够在组织中对数据生产者和消费者之间产生的数据进行编目、发现、分析、共享和管理。 通过 Amazon DataZone&#xff0c;数据生产者可使用 Amazon Glue 数据目录和 Amazon Redshift 表格中的结构化数据资…
阅读更多...
如何优化模型渲染性能

如何优化模型渲染性能

1、提高模型渲染性能的好处 优化模型渲染性能有以下几个好处&#xff1a; 提高用户体验&#xff1a;良好的模型渲染性能可以使图形应用程序更加流畅和响应快速。当模型以较高的帧率渲染时&#xff0c;用户可以获得更流畅、更真实的视觉效果&#xff0c;提升整体的用户体验。 …
阅读更多...
Jmeter性能测试（压力测试）

Jmeter性能测试（压力测试）

1.先保存 2.添加请求&#xff08;即添加一个线程组&#xff09; 3.添加取样器&#xff08;在线程组下面添加一个http请求&#xff09; 场景1&#xff1a;模拟半小时之内1000个用户访问服务器资源&#xff0c;要求平均响应时间在3000毫秒内&#xff0c;且错误率为0&#xff0…
阅读更多...
BI工具-DataEase(2) 基础使用

BI工具-DataEase(2) 基础使用

先讲下工具栏,分别是仪表盘,数据集,数据源,模板市场等等. 和大多数的BI工具一样,首先配置的就是数据源 1. 数据源:支持OLTP,OLAP,数仓/数据湖,我们这边还是使用的mysql 新建mysql数据源,填写配置信息 2. 数据集支持Excel,SQL,关联数据集等等,新建SQL数据集,输出SQL语句 点击运…
阅读更多...
软考-面向对象技术

软考-面向对象技术

面向对象的基本概念 对象&#xff1a;属性&#xff08;数据&#xff09; 方法&#xff08;操作&#xff09; 对象ID类&#xff08;实体类、控制类/边界类&#xff09;继承与泛化&#xff1a;复用机制封装&#xff1a;隐藏对象的属性和实现细节&#xff0c;仅对外公开接口多态&…
阅读更多...
【JavaEE】Callable 接口

【JavaEE】Callable 接口

Callable 是一个 interface . 相当于把线程封装了一个 “返回值”. 方便程序猿借助多线程的方式计算结果. 实现Callable也是创建线程的一种方法&#xff01;&#xff01;&#xff01;&#xff01; Callable的用法非常接近于Runnable&#xff0c;Runnable描述了一个任务&#…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023