一、方法简介
通过一个点复数序列求出两个
点实数序列的离散傅里叶变换,进一步提升快速傅里叶变换的效率。
二、方法详解
和
是实数序列,且长度都为
,定义复数序列:
,
则序列和
可表示为:
的离散傅里叶变换可表示为:
序列和
可表示为:
因为,所以:
三、MatLab代码示例
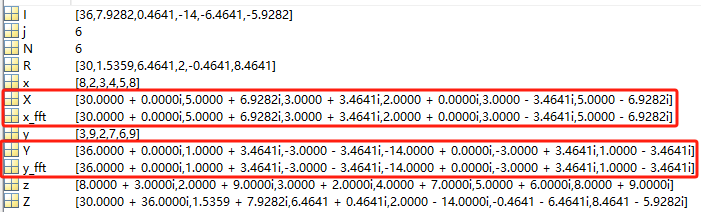
x = [8 2 3 4 5 8];
y = [3 9 2 7 6 9];
x_fft = fft(x);
y_fft = fft(y);
z = x+1i*y;
Z = fft(z);
N = length(Z);
X = zeros(1,N);
Y = zeros(1,N);
R = real(Z);
I = imag(Z);
X(1) = R(1);
Y(1) = I(1);
for j = 2 : N
X(j) = 1/2*(Z(j)+conj(Z(N+2-j)));
Y(j) = -1i/2*(Z(j)-conj(Z(N+2-j)));
end运行结果: