---

第一部分：栈

1、栈的定义

只允许在一端进行插入或删除操作的线性表，四个字：“后进先出”
向栈中插入元素称为入栈，从栈中删除元素称为出栈。

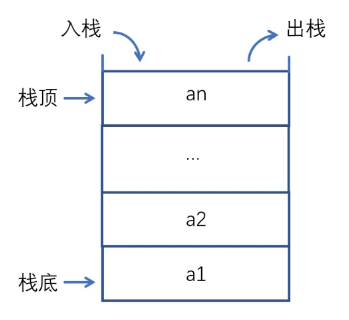
2、栈的操作

空栈状态	入栈操作	满栈状态	出栈操作
top = -1	① top = top+1； ② A[top] = a；	top = Maxsize-1	① e = A[top]； ② top = top-1；

• “上溢”现象——当栈满时，再作进栈运算产生空间溢出的现象；
• “下溢”现象——当栈空时，再作退栈运算产生空间溢出的现象。

第一部分习题

1. 若已知一个栈的入栈序列是1，2，3…，n，其输出序列为p1， p2，p3…， pn，若 p1=n，则 pi 为（C）。
   A.i
   B.n=i
   C.n-i+1（代数法得p2是n-1、p3是n-2，则归纳法得n-i+1）
   D.不确定

2. 元素a1、a2、a3、a4依次进入顺序栈，则下列不可能的退栈序列是（D）。
   A.a4，a3，a2，a1（全部入栈后依次出栈）
   B.a3，a2，a4，a1（先入栈 a1-a3，然后出栈 a3 和 a2，再入栈 a4，最后依次出栈）
   C.a3，a4，a2，a1（先入栈 a1-a3，然后出栈 a3 ，再入栈 a4，最后依次出栈）
   D.a3，a1，a4，a2（很明显要出栈 a2 后才能出栈 a1）

3. 设有一顺序栈S，元素s1、s2、s3、s4、s5、s6依次入栈，如果6个元素出栈的顺序是s2、s3、s4、s6、s5、s1，则栈的容量至少应该是（3）。-填空题
   【分析】：栈内最多同时存储了s6、s5、s1

---

第二部分：共享栈

1、共享栈的定义

共享栈又叫做双栈∶
两个栈共同并辟一个存储空间，让一个栈的栈底为该空间的始端（下标0），另一栈的栈底为该空间的末端（下标Maxsize-1）。当元素进栈时，都从两端向中间延伸，这样能够使剩余的空间为任意一个栈所使用。

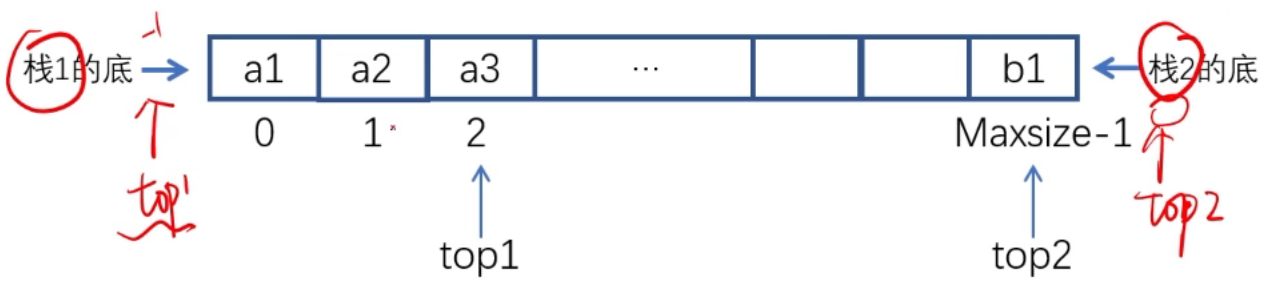
2、共享栈的操作

• 栈空: top1 = -1； top2 = Maxsize；
• 栈满；top1 = top2-1时（top1+1 = top2也可）；
• 栈1的操作：
  • 入栈：① top1 = top1+1（向栈1顶移动）；② A[top1] = val；
  • 出栈：① e = A[top1]； ② top1 = top1-1（向栈1底移动）;
• 栈2的操作：
  • 入栈：① top2 = top2-1（向栈2顶移动）；② A[top2] = val；
  • 出栈：① e = A[top2]；② top2 = top2+1（向栈2底移动）；

第二部分习题

1. 为了减小栈溢出的可能性，可以让两个栈共享一片连续存储空间，两个栈的栈底分别设在这片空间的两端，这样只有当（A）时才可能产生上溢。
   A.两个栈的栈顶在栈空间的某一位置相遇
   B.其中一个栈的栈顶到达栈空间的中心点
   C.两个栈的栈顶同时到达栈空间的中心点（不可能出现的情况，或者说此时已经处于上溢）
   D.两个栈均不空，且一个栈的栈顶到达另一个栈的栈底（因为另一个栈不为空，所以最多到达栈底的前一个位置，和C中类似）

2. 若栈采用顺序存储方式存储，现两栈共享空间V[1，…，m]，top[1]、top[2]分别代表第1和第2个栈的栈顶，栈1的底在V[1]，栈2的底在V[m]，则栈满的条件是（B）。
   A.$|$top[2]-top[1]$|$ = 0
   B.top[1]+1 = top[2]（共享栈栈满的定义）
   C.top[1]+top[2] = m
   D.top[1] = top[2]

---

第三部分：链栈

1、链栈的定义

前面提到的栈和共享栈都是采用顺序存储的方式实现，如果是采用链式存储的方式实现的栈，我们称其为链栈。
其实链表实现的栈是对链表施加了一个“后进先出”约束，其结构和一般的链表是完全相同的。

2、链栈的操作

需要注意，在前面顺序栈中top指的是数组下标，而链栈中top指的是指针。

• 栈空：top = null；
• 栈满：不存在滴！
• 入栈：（其实就是链表的头插法）
  ① p->next = top；
  ② top = p；
• 出栈：
  ① e = top->data；（p = top;）
  ② top = top->next；（free(p);）

第三部分习题

1. 向一个栈顶指针为top的链栈中插入一个x结点，则执行（C）。
   A.top->next=x
   B.x->next=top->next；top->next=x
   C.x->next=top；top=x
   D.x->next=top；top=top->next

2. 如果以链表作为栈的存储结构，则退栈操作时（D） 。
   A.必须判别栈是否满（链栈不存在栈满，除非是物理存储空间严重不足；且栈满是在入栈操作时判断）
   B.对栈不作任何判别（不做判断健壮性不足）
   C.判别栈元素的类型（没有意义）
   D.必须判别栈是否空

---

第一到三部分小结

1、顺序栈和链栈的比较

（1）时间性能比较
顺序栈和链栈的基本操作的算法，时间复杂度均为O(1)。
（2）空间性能比较
初始时顺序栈必须确定一个固定的长度，所以有存储元素个数的限制和空间浪费的问题。
链栈无栈满问题，只有当内存没有可用空间时才会出现栈满，但是每个元素都需要一个指针域,从而产生了结构性开销。

• 一般结论：当栈在使用过程中元素个数变化较大时（即难以确定固定的长度），用链栈比较好；反之，应该采用顺序栈。
• 经典例题：和顺序栈相比，链栈有一个比较明显的优势是（A）。
  A.通常不会出现栈满的情况
  B.通常不会出现栈空的情况
  C.插入操作更容易实现
  D.删除操作更容易实现

2、栈的应用

• 栈的应用：主要在括号匹配、表达式求值、递归中前缀表达式和后缀表达式。
• 经典例题：中缀表达式$A-(B+C/D)\ast E$的后缀形式是（D）。
  A.$AB-C+D/E\ast$
  B.$ABC+D/-E\ast$
  C.$ABCD/E\ast +-$
  D.$ABCD/+E\ast -$

【分析】中缀表达式就是我们常见的运算符号在式子中间的算术式，比较难的是如何将其转化为前缀表达式和后缀表达式，即运算符号在式子的前端或后端的算术式：

① 加括号：按照运算符优先级将每一步运算都用括号括起来，原括号>乘除>加减，即上式变为：$(A-((B+(C/D))\ast E))$；
② 移符号：将运算符移到括号前或括号后，即继续变为：$-(A\ast (+(B/(CD))E))$或$(A((B(CD)/)+E)\ast )-$；
③ 去括号：把括号去除得到前缀表达式：$-A\ast +B/CDE$，或后缀表达式：$ABCD/+E\ast -$。

3、栈的应用相关习题

1. 将一个递归算法改为对应的非递归算法时，通常需要使用（A）
   A.栈（通常使用栈，也可以使用其他方法）
   B.队列
   C.循环队列
   D.优先队列

2. 算术表达式$A+B\ast C-D/E$转为前缀表达式后为（D） 。
   A.$-A+B\ast C/DE$
   B.$-A+B\ast CD/E$
   C.$-+\ast ABC/DE$
   D.$-+A\ast BC/DE$
   【分析】① $((A+(B\ast C))-(D/E))$；② $-(+(A\ast (BC))/(DE))$；③ $-+A\ast BC/DE$；

3. 中缀表达式$A\ast (B+C)/(D-E+F)$的后缀表达式是（C） 。
   A.$A\ast B+C/D-E+F$
   B.$AB+C+D/E-F+$
   C.$ABC+\ast DE-F+/$
   D.$ABCDEF\ast +/-＋$
   【分析】① $((A\ast (B+C))/((D-E)+F))$；② $((A(BC)+)\ast ((DE)-F)+)/$；③ $ABC+\ast DE-F+/$；

---

第四部分：队列

1、队列的定义

只允许在表的一端进行插入，而在表的另一端进行删除。四个字：“先进先出”
向队列中插入元素称为入队，从队列中删除元素称为出队。

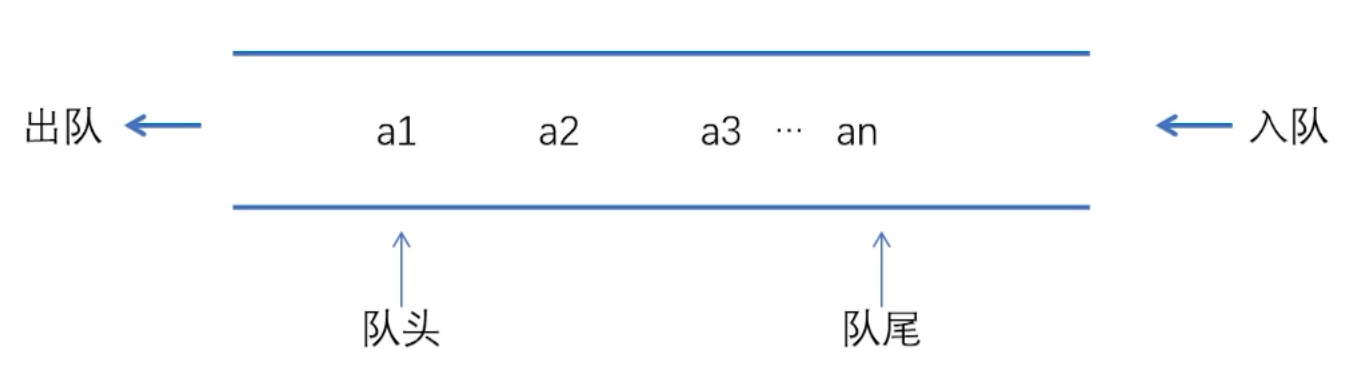
【注意】简单队列可能存在假溢出或假满的问题，即：当一个满队列的队头元素出队后，虽然队头指针前产生了空位，但入队必须从队尾进行，而此时队尾指针已经达到最末端，无法后移（判定为队满）导致无法进行入队操作。

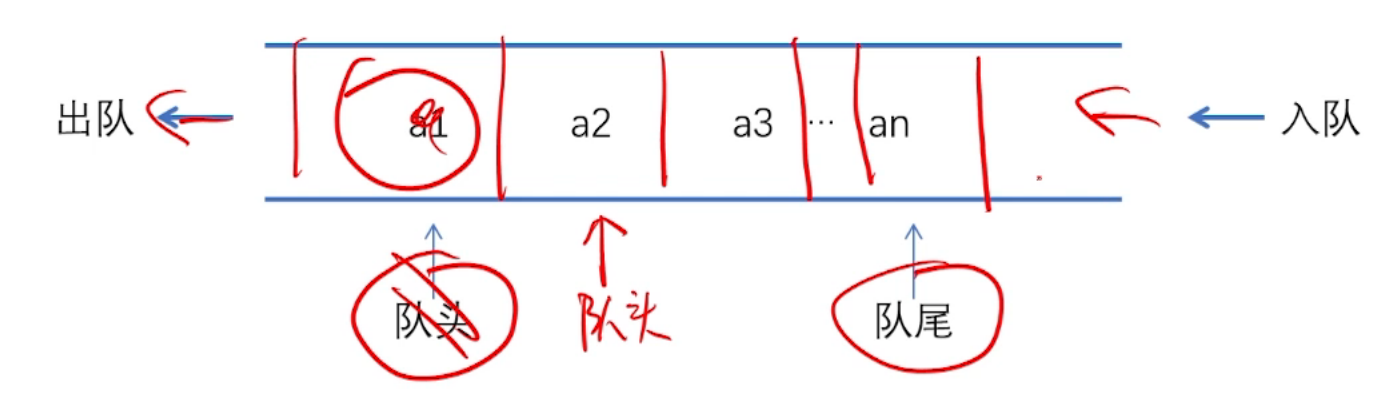
2、循环队列

为了解决假溢出或假满这一问题，一般将顺序队列组成循环队列。循环队列就是将队列的队首和队尾连接在一起，当然这只是一种逻辑结构，本质上还是顺序存储，实现的方法就是当队尾指针达到队列的最大位置时，再前进就回到队列起始位置。

3、循环队列的操作

空队状态	入队操作	满队状态	出队操作
front = rear	① queue[rear] = A； ② rear = (rear+1)%Maxsize；	(rear+1)%Maxsize = front	① e = queue[front]； ② front = (front+1)%Maxsize；

• 上述操作中，对Maxsize取余是为了能够在到达队尾时+1回到队首。

第四部分习题

1. 假设以数组 A[m] 存放循环队列的元素，其头尾指针分别为 front 和 rear，则当前队列中的元素个数为（A） 。
   A.(rear-front+m)%m
   B.rear-front+1
   C.(front-rear+m)%m
   D.(rear-front)%m
   【分析】因为 rear 是不可能超过 front 的，所以二者之间的差距最大为 m；用二者之差加上 m，若差值为正，取余运算将消去所加的 m；若差值为负，取余运算不会生效，该式相当于$(m+rear)-front$。

2. 设栈 S 和队列 Q 的初始状态为空，元素 a、b、c、d、e、f 依次通过栈 S，一个元素出栈后即进队列 Q，若6个元素出队的序列是 a、c、f、e、d、b，则栈S的容量至少应该是（C）。
   A.6
   B.5
   C.4
   D.3
   【分析】栈内最多的时候存储了b、d、e、f

3. 若用一个大小为6的数组来实现循环队列，且当前 rear 和 front 的值分别为0和3，当从队列中删除一个元素，再加入两个元素后，rear和front的值分别为（B）。
   A.1和5
   B.2和4
   C.4和2
   D.5和1

---

第五部分：双端队列

1、双端队列的定义

指允许两端都可以进行入队和出队操作的队列（两端不受限）

• 输出受限的双端队列：允许在一端进行插入和删除，但在另一端只允许插入的双端队列称为输出受限的双端队列.
• 输入受限的双端队列：允许在一端进行插入和删除，但在另一端只允许删除的双端队列称为输入受限的双端队列.

2、双端队列的操作

与普通队列相同，在不受限的情况下可以对两端进行入队、出队操作。

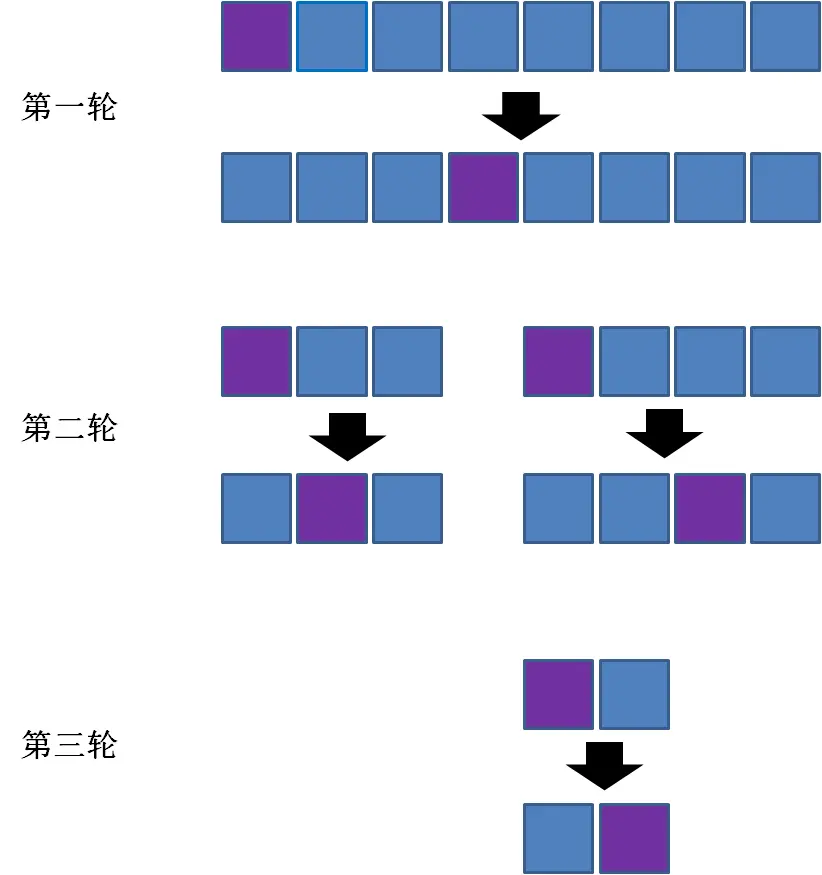
• 要注意如果两端都进行了入队操作，会导致先入队的元素被包围在双端队列中间。此时从某一端出队，变成了出口端入队的部分“后进先出”，入口端入队的部分“先进先出”。（输出受限）
• 同样的如果只从某一端入队，却从两端出队，就变成了入口端出队的部分“后进先出”，出口端出队的部分“先进先出”。（输入受限）

【经典例题】若以1234作为双端队列的输入序列，既不能由输入受限的双端队列得到，也不能由输出受限的双端队列得到的输出序列的是（B）。
A.4213
B.4231
C.4132
D.1234

---

第六部分：链队

1、链队的定义

实际上是一个同时带有队头指针和队尾指针的单链表，相当于我们对链表施加了一个“先进先出”的约束。

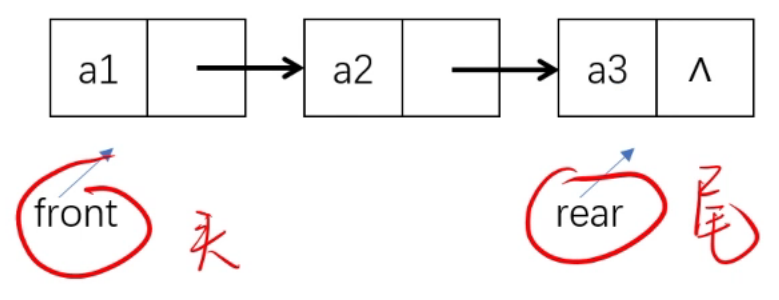
2、链队的操作

需要注意，在前面顺序存储的队列中，front 和 rear 指的是数组下标，而链队中二者都是指针。

• 空队：front = null；rear = null；
• 满队：不存在滴！
• 入队：（其实就是链表的尾插法）
  ① rear->next = p；
  ② rear = rear->next；
• 出队：
  ① e = front->data；（p = front;）
  ② front = front->next；（free(p);）

第六部分习题

1. 若用单链表来表示队列，则应该选用（B）。
   A.带尾指针的非循环链表（回到队首实现出队操作，过于耗时×）
   B.带尾指针的循环链表（尾插入队，然后循环到队首出队√）
   C.带头指针的非循环链表（去到队尾实现入队操作，过于耗时×）
   D.带头指针的循环链表（同样需要一个一个结点移到队尾，除非是双循环链表×）

2. 判定“带头结点的链队列为空”的条件是（A） 。
   A.Q.front == NULL（头指针用于出队，一般指向队首元素）
   B.Q.rear == NULL（尾指针用于入队，本来就指向空）
   D.Q.front == Q.rear（可能是含有一个结点）
   D.Q.front != Q.rear

---

第四到六部分小结

1、循环队列与链式队列的比较

（1）时间性能比较
循环队列与链式队列基本操作的算法都需要常数时间O(1)，

• 循环队列是事先申请好空间，使用期间不释放，
• 链式队列是每次申请和释放结点也会存在一些时间开销，

如果入队出队频繁，则两者还是有细微差异——最好选择循环队列，可以节省申请和释放结点的时间开销。

（2）空间性能比较
循环队列必须有一个固定的长度（顺序存储），所以就有了存储元素个数和空间浪费的问题。

2、队列的应用

• 队列的应用：主要在层次遍历中，另外队列应用于计算机系统中可解决主机与外部设备之间速度不匹配的问题和多用户引起的资源竞争问题。
• 经典例题：在解决计算机主机与打印机之间速度不匹配问题时通常设置一个打印数据缓冲区，这样主机将要输出的数据依次写入该缓冲区，而打印机则从该缓冲区中取出数据打印。该缓冲区应该是一个（B）结构。
  A.堆栈
  B.队列
  C.数组
  D.线性表

---

栈和队列小结

• 栈在数据结构中考察占比较大，队列则主要在操作系统中考察占比较大。