1.前言
位运算在我们刷题时候,对于效率和空间都是很大的提升,所以位运算符,对于我们的作用也是不可或缺的。
里面就存在一个很重要的思想就是位图,此次我讲解位运算符的作用主要是为他服务的
位图的原理:通过一个整数模拟,四个字节三十二个比特位的数组就形成了,这种做可以在时间复杂度为O(1)的情况下使用hash表来解答问题。而你所进行的位数相加减,我将在下面介绍、
2.介绍概念
- 按位与(&):将两个操作数的对应位进行逻辑与运算,相同位置上的位都为1时,结果为1,否则为0。
- 按位或(|):将两个操作数的对应位进行逻辑或运算,相同位置上的位只要有一个为1,结果即为1。
- 按位异或(^):将两个操作数的对应位进行逻辑异或运算,相同位置上的位不同时,结果为1,否则为0。
- 按位取反(~):对操作数的每个位进行取反操作,即0变为1,1变为0。
此外,还有一些位移运算符:
- 左移(<<):将一个操作数的所有位向左移动指定的位数,右侧空出的位用0填充。
- 有符号右移(>>):将一个操作数的所有位向右移动指定的位数,移位后左侧空出的位用符号位填充,即正数用0填充,负数用1填充。
- 无符号右移(>>>):将一个操作数的所有位向右移动指定的位数,移位后左侧空出的位用0填充,不考虑符号位。
下面我来介绍一下,我对位运算的记忆方式吧!!!!
1.按位与(&):有 0 就是 0
2 .按位或(|) : 有1 就是 1
3 .按位异或(^): 同为 0 异为 1 (也可以记成 无进位相加)
4.按位取反(~):0 变 1 1变0
下面也有一些注意事项:
位运算符只适用于整数类型(byte、short、int、long)和char类型,不适用于浮点数类型(float、double)和布尔类型(boolean)。
3.位运算符的作用
3.1. 异或(^)符的运算律
3.1.1.无进位相加
因为^同为0嘛,所以说 0 + 0 = 0 1 + 1 = 0 1 + 0 = 1 所以就实现了无进位相加
我在后面还会介绍一下,不用+怎么实现两数相加来介绍这个概念
3.1.2.消消乐
消消乐概念:就是n ^ n = 0 0 ^ n = 0
3.1.3. 交换律和结合律
a ^ b ^ c = a ^ ( b ^ c )
原理分析:
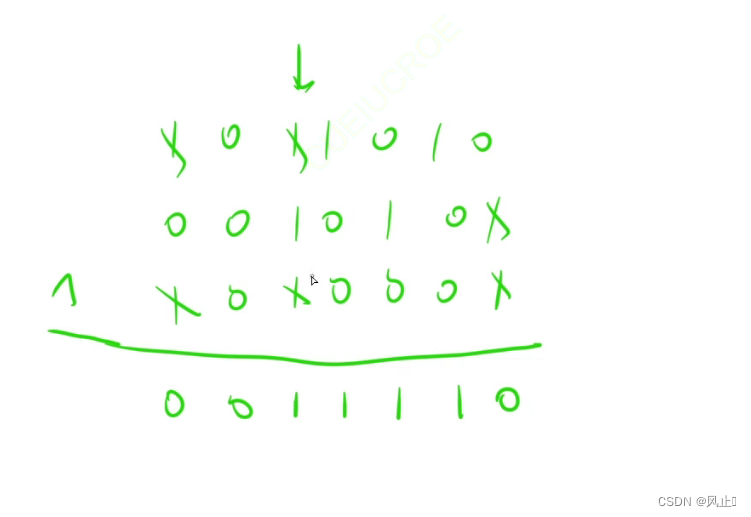
这个原理还是根据3.1.1无进位相加, 0 + 0 = 0 1 + 1 = 0 1 + 0 = 1 本质就是在做 1 的抵消。所以在加的时候任意抵消1
然后我推荐几道题可以使用此知识点解决
力扣 136.只出现一次的数字
260.只出现一次的数字III
3.2.判断第x位为 0 还是 1
n = (n >> x)& 1
为什么是这样呢,我将在下面介绍原理:

右移后就是把你要判断的位置,移动到了最后一位,此时与 1 就相当于其他位置清0(&有0则0,1除了最后一位全是0),最后一位是1答案是1 是0答案是0
3.3.将第x位修改成1
n = n | (1 << x)
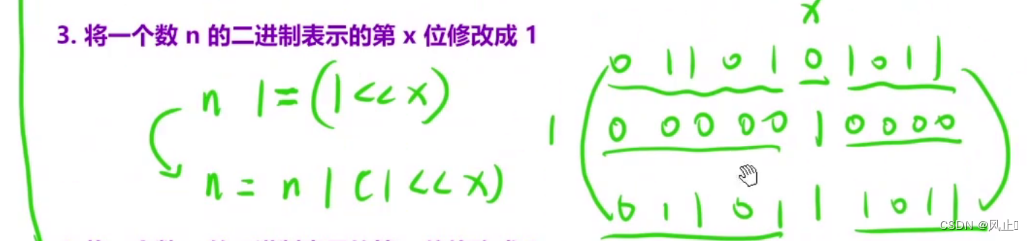
此时1左移x位就像等于和你修改的位置对齐了,此时 或 1 就是其他位置不变(1<<x就是此时除了x位置是1其他均为0,|有1则1,遇0不变),只有第x位,无论是什么都会变成1.
3.4. 将第x位修改成0
n = n & n (~(1 << x))

这个的原理就跟上述的类似:此时取反就是让x位置变成0其余位置变成1,然后进行 按位与的时候第x位会变成0(因为有0则0嘛)
3.5.位图的思想
注意这个才是重中之重,前面之所以引出这么多概念,都是为了这个概念模型服务的。
位图的本质:就是一个hash表,只不过现在用比特位代替数组,让每一个比特位(0 1)来记录我们信息,所以就可以使用一个整数来实现我们的增删查改。

为什么说上面都是为了位图而服务的呢?
因为我们如果这样模拟hash表,我们就需要经常看看你某一位存的是0还是1,我想修改你我怎么操作
在最后我会通过一道题,来加深大家对位图的理解。
3.6.提取最低位的1 (lowbite)
n & -n

主要思想就是 & -n (会将最后一个1右边的部分全部变成相反,左边不变)
又因为& 有0则0 右边全是相反代表必有一个0 ,所以全变成0了
3.7.干掉最右侧的1
n & (n - 1)

主要思想就是 & -n (会将最后一个1和它左边的部分全部变成相反,右边不变)
又因为& 有0则0 左边全是相反代表必有一个0 ,所以全变成0了,就把最后一个1干掉了
4.例题分析
4.1位运算符实现相加
这一题的主要思路:就是(a & b) << 1实现进位,来弥补^ 的无进位相加
public static int add(int a, int b) {
while (b != 0) {
int carry = (a & b) << 1; // 进位
a = a ^ b; // 加法
b = carry; // 迭代
}
return a;
}4.2判断字符是否为1
我在下面先介绍hash表怎么解答的在书写位图的代码,大家自行对比,因为位图空间复杂度为O(1).
hash表实现
//解法一:hash表
public boolean isUnique1(String str) {
if(str.length() > 26){ // 利用鸽巢原理来做优化
return false;
}
int[] hash = new int[26];//创建一个hash表用来存储字符
char[] charArray = str.toCharArray();
for (char c : charArray) {//添加字符
if (hash[c - 'a'] != 0){
return false;
}else {
hash[c - 'a']++;
}
}
return true;
}位图实现
//解法二:利用位图
public boolean isUnique(String str) {
if (str.length() > 26) { // 字符串超过26必为false
return false;
}
int hash = 0;//利用位图模拟hash表
char[] charArray = str.toCharArray();
for (char c : charArray) {//添加字符
int index = c - 'a';//位图要存的索引
if ((hash & (1 << index)) != 0){
return false;
}else {
hash |= (1 << index);
}
}
return true;
}后面的就不一一介绍了,推荐几道题
191.位1的个数
338、比特位计教
461、汉明距离