小波分解C++版本

C++代码

参考了一些Github的代码
最终代码可从链接下载。
main函数如果打不开的话，使用

#include <iostream>
#include <vector>
#include <fstream>
#include "wavelet.h"

int main() {
    // 读取原始信号数据
    std::ifstream input("MultiSinWaveWithNoise_1s.txt");
    if (!input.is_open()) {
        std::cerr << "Failed to open input file." << std::endl;
        return 1;
    }

    std::vector<double> original_signal;
    double value;
    while (input >> value) {
        original_signal.push_back(value);
    }
    input.close();

    // 初始化小波对象，使用 db4 小波，从matlab导出
    std::vector<double> Hi_D = { -0.230377813308855,0.714846570552542,-0.630880767929590,-0.027983769416984,0.187034811718881,0.030841381835987,-0.032883011666983,-0.010597401784997 };
    std::vector<double> Hi_R = { -0.010597401784997,-0.032883011666983,0.030841381835987,0.187034811718881,-0.027983769416984,-0.630880767929590,0.714846570552542,-0.230377813308855 };
    std::vector<double> Lo_D = { -0.010597401784997,0.032883011666983,0.030841381835987,-0.187034811718881,-0.027983769416984,0.630880767929590,0.714846570552542,0.230377813308855 };
    std::vector<double> Lo_R = { 0.230377813308855,0.714846570552542,0.630880767929590,-0.027983769416984,-0.187034811718881,0.030841381835987,0.032883011666983,-0.010597401784997 };

    Wavelet<double> wavelet(Lo_D, Hi_D, Lo_R, Hi_R);

    // 进行小波分解
    int levels = 3; //5;
    Decomposition1D<double> decomposition = wavelet.Wavedec(original_signal, levels);

    // 对细节系数进行软阈值去噪，阈值设为1或0.5等，根据实际情况调整

    double threshold_V01 = 1; // 0.5;

    for (size_t i = 0; i < decomposition.NumLevels(); ++i) {
        std::vector<double> detcoef = decomposition.GetDetcoef(i);
        for (size_t j = 0; j < detcoef.size(); ++j) {
            if (std::abs(detcoef[j]) < threshold_V01) {
                detcoef[j] = 0.0;
            }
        }
        decomposition.SetDetcoef(detcoef, i);
    }

    // 重构信号
    std::vector<double> denoised_signal = wavelet.Waverec(decomposition, original_signal.size());

    // 将去噪后的信号保存到文件
    std::ofstream output("denoised_signal.txt");
    if (!output.is_open()) {
        std::cerr << "Failed to open output file." << std::endl;
        return 1;
    }

    for (size_t i = 0; i < denoised_signal.size(); ++i) {
        output << denoised_signal[i] << std::endl;
    }
    output.close();

    std::cout << "Denoised signal saved to denoised_signal.txt" << std::endl;

    return 0;
}

Matlab生成小波系数代码

[Lo_D, Hi_D, Lo_R, Hi_R] = wfilters('db4');

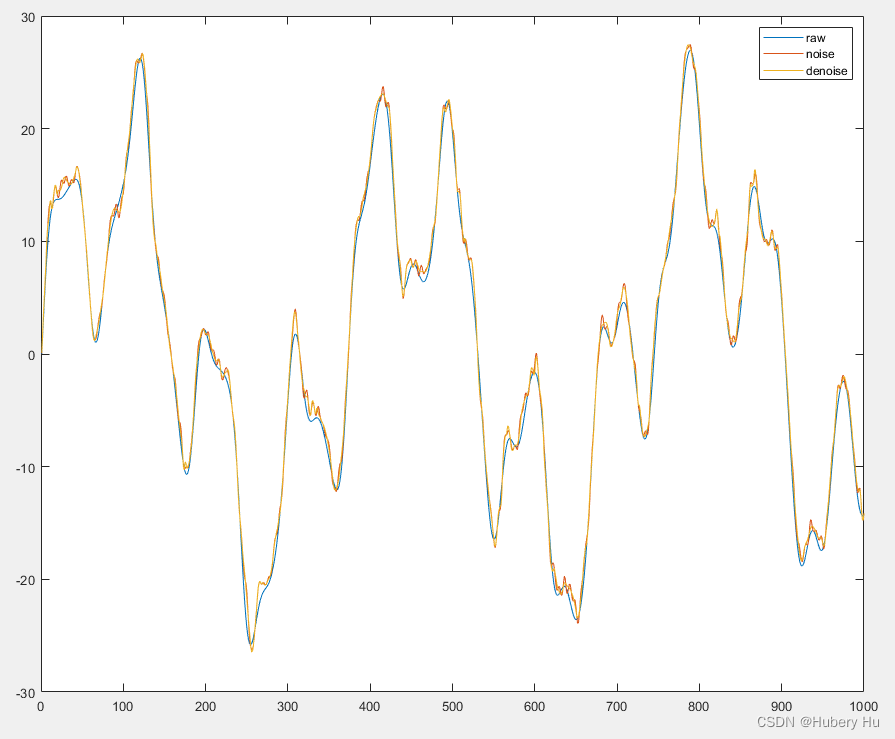
去噪效果

%%
clear all;
clc;

% denoised_result = load('VS_result\denoised_result01.txt');
% denoised_result = load('VS_result\denoised_result04.txt');

% denoised_result = load('VS_result\denoised_signal01.txt');
denoised_result = load('VS_result\denoised_signal05.txt');

%%
data = load('MultiSinWaveWithNoise_1s.txt');
% data = load('MultiSinWaveWithNoise_10s.txt');

fs=1000;%采样频率是1000Hz
yourEEGData = data;

%生成正弦波信号
t=linspace(0, length(data)/fs-1/fs, length(data));
y1 =15*sin(2*pi* 2.8 *t);%生成频率为2.8Hz，幅值为15的正弦波
y2 =10*sin(2*pi* 10.5 *t);%生成频率为10.5Hz，幅值为10的正弦波
y3 =3*sin(2*pi* 27 *t);%生成频率为27Hz，幅值为3的正弦波
y4 =0.5*sin(2*pi* 43 *t);%生成频率为43Hz，幅值为0.5的正弦波

y_Sin =y1+y2+y3+y4;


%%
figure;
plot(y_Sin);
hold on;
plot(data);
hold on;
plot(denoised_result);
legend({'raw','noise','denoise'});

error_noise = sum(abs(data-y_Sin'));
error_denoise = sum(abs(denoised_result-y_Sin'));

Matlab自带小波去噪代码

%%
clear all;
clc;

%%
data = load('MultiSinWaveWithNoise_1s.txt');
% data = load('MultiSinWaveWithNoise_10s.txt');

fs=1000;%采样频率是1000Hz
yourEEGData = data;

%生成正弦波信号
t=linspace(0, length(data)/fs-1/fs, length(data));
y1 =15*sin(2*pi* 2.8 *t);%生成频率为2.8Hz，幅值为15的正弦波
y2 =10*sin(2*pi* 10.5 *t);%生成频率为10.5Hz，幅值为10的正弦波
y3 =3*sin(2*pi* 27 *t);%生成频率为27Hz，幅值为3的正弦波
y4 =0.5*sin(2*pi* 43 *t);%生成频率为43Hz，幅值为0.5的正弦波

y_Sin =y1+y2+y3+y4;

%%
% 1. 读取脑电信号数据
% 请将您的脑电信号数据加载到MATLAB中，例如，使用load函数。

% 2. 小波分解
% 选择适当的小波函数和分解级别
signal = yourEEGData; % 替换为您的脑电信号数据
waveletName = 'db4'; % 小波类型，可以根据需要更改
level = 5; % 分解级别，可以根据需要更改
[C, L] = wavedec(signal, level, waveletName);

% 3. 去除噪声
% 选择适当的阈值和去噪方法
threshold = 0.5; % 阈值，可以根据需要更改
denoisedCoeff = wthresh(C, 's', threshold);

% 4. 重构信号
denoisedSignal = waverec(denoisedCoeff, L, waveletName);

% 5. 绘制原始信号和去噪后的信号
% figure;
% subplot(2, 1, 1);
% plot(signal);
% title('Raw');
% 
% subplot(2, 1, 2);
% plot(denoisedSignal);
% title('Denoise');

% 6. 分析和评估结果
% 根据需要，您可以进行进一步的分析和评估，以确保去噪效果满意。

% 7. 保存去噪后的信号
% 如果需要，可以将去噪后的信号保存到文件。

% 请根据您的数据和需求调整代码中的参数和细节。

%%
figure;
plot(signal);
hold on;
plot(denoisedSignal);

error_denoise = sum(abs(denoisedSignal - y_Sin'));
error_before = sum(abs(signal - y_Sin'));

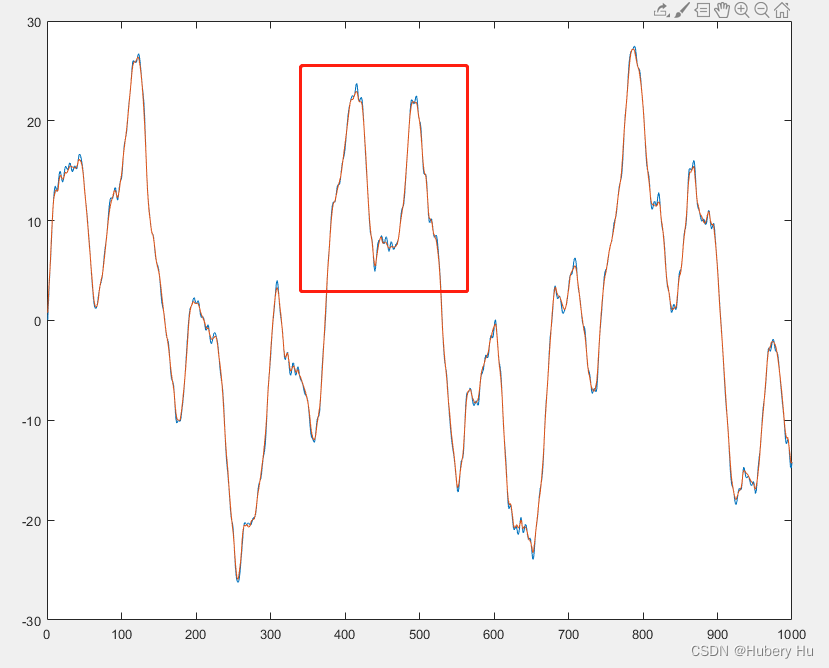
Matlab自带函数去噪效果更好，改写的C++因为计算精度和逻辑有所差异，但改变软阈值的值或者改成硬阈值去噪法也能改善结果。