恶魔们抓住了公主并将她关在了地下城 dungeon 的 右下角 。地下城是由 m x n 个房间组成的二维网格。我们英勇的骑士最初被安置在 左上角 的房间里，他必须穿过地下城并通过对抗恶魔来拯救公主。

骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下，他会立即死亡。

有些房间由恶魔守卫，因此骑士在进入这些房间时会失去健康点数（若房间里的值为负整数，则表示骑士将损失健康点数）；其他房间要么是空的（房间里的值为 0），要么包含增加骑士健康点数的魔法球（若房间里的值为正整数，则表示骑士将增加健康点数）。

为了尽快解救公主，骑士决定每次只 向右 或 向下 移动一步。

返回确保骑士能够拯救到公主所需的最低初始健康点数。

注意：任何房间都可能对骑士的健康点数造成威胁，也可能增加骑士的健康点数，包括骑士进入的左上角房间以及公主被监禁的右下角房间。

示例 1：

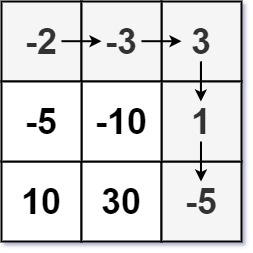
输入：dungeon = [[-2,-3,3],[-5,-10,1],[10,30,-5]]
输出：7
解释：如果骑士遵循最佳路径：右 -> 右 -> 下 -> 下 ，则骑士的初始健康点数至少为 7 。

示例 2：

输入：dungeon = [[0]]
输出：1

提示：

• m == dungeon.length
• n == dungeon[i].length
• 1 <= m, n <= 200
• -1000 <= dungeon[i][j] <= 1000

思路一：动态规划

c++解法

class Solution {
public:
    int calculateMinimumHP(vector<vector<int>>& dungeon) {
        int m = dungeon.size(),n = dungeon[0].size();
        vector<vector<int>> dp(m,vector<int>(n,0));
        dp[m-1][n-1] = dungeon[m-1][n-1];
        for(int i = m-2;i>=0;i--){
            dp[i][n-1] = min(dungeon[i][n-1],(dp[i+1][n-1]+dungeon[i][n-1]));
        }
        for(int j = n-2;j>=0;j--){
            dp[m-1][j] = min(dungeon[m-1][j],(dp[m-1][j+1]+dungeon[m-1][j]));
        }
        for(int i = m-2;i>=0;i--){
            for(int j = n-2;j>=0;j--){
                dp[i][j] = min(dungeon[i][j],max(dp[i+1][j],dp[i][j+1])+dungeon[i][j]);
            }
        }
        return dp[0][0]>0?1:-1*dp[0][0]+1;
    }
};

分析：

本题要计算到达右下角的最少起始点数，可以利用动态规划的方法每向右或向左走一步则比较右边和下边哪个更小，动态规划则将下一步比较新步的初始步和右下三种情况的最小值来计算dp[i][j]值，最后返回dp[0][0]，并判断是否大于零，若大于则返回1；

总结：

本题考察动态规划的应用，找到状态方程后可解决，时间复杂度为O(n^2)，空间复杂度为O(n^2)