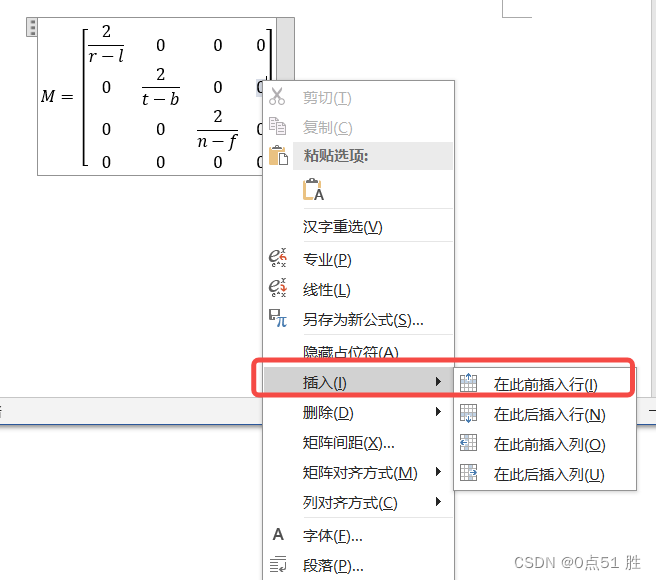
所谓正交投影变换，就是已知盒状可视空间内任意点坐标(x,y,z)，求解垂直投影到xy平面的对应点坐标。
按照这个定义，xyz坐标系本身就是正交坐标系，盒状可视空间内任意点的坐标(x,y,z)投影到(x,y)平面，只要简单地丢弃z坐标就可以啦，即(x,y,z)变换到(x,y,0)即可，这个理解完全没有问题，但却不是正确的结果，那么原因是什么呢？

主要原因是有两个需要考虑的问题：

规范化坐标系：现实情况几乎所有的图形系统都把坐标系的空间范围限定在(-1,1)范围内，这么做是为了方便移植，使坐标系独立于各种尺寸的图形设备。
z坐标需要保留：想象一下可视空间内存在多个物体的场景，前面的物体可能遮挡后面的物体导致无法被看见，绘制图像时需要利用z坐标来判断前后遮挡关系来觉得那个物体需要绘制，因此保留z坐标是最终图形呈现所必须的参数。

所以正交投影变化起始就是把选择的一个矩形区域缩放平移到标准位置和大小。
知乎这篇文章计算的应该是 opengl 的公式，opengl 的标准位置和大小是 [-1,1]^3。

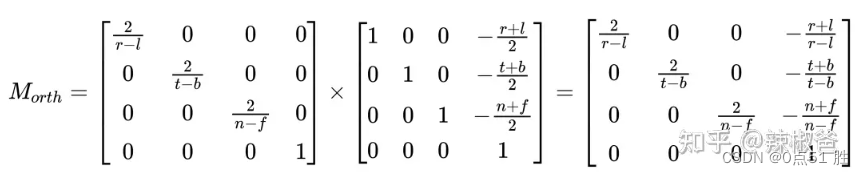
directX3d 正交投影矩阵

directX3D 的标准位置是 xy 的范围是 [-1,1]^2，z的范围是[0,1]，所以 directX3D 的正交投影公式是下面这个。

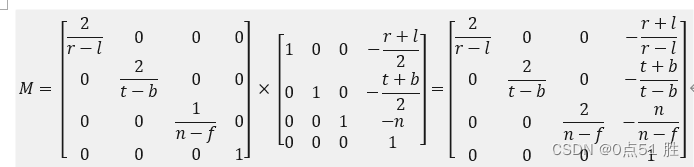
XMMatrixOrthographicLH 的计算公式和上面也是对应的(directX和oepngl的横纵也是反的，所以需要转置一下)
XMMatrixOrthographicLH 框起来的范围应该是x:(-viewWidth/2, viewWidth/2),y:(-viewHeight/2,viewHeight/2),z:(nearZ, farZ)

float fRange = 1.0f / (FarZ - NearZ);

XMMATRIX M;
M.m[0][0] = 2.0f / ViewWidth;
M.m[0][1] = 0.0f;
M.m[0][2] = 0.0f;
M.m[0][3] = 0.0f;

M.m[1][0] = 0.0f;
M.m[1][1] = 2.0f / ViewHeight;
M.m[1][2] = 0.0f;
M.m[1][3] = 0.0f;

M.m[2][0] = 0.0f;
M.m[2][1] = 0.0f;
M.m[2][2] = fRange;
M.m[2][3] = 0.0f;

M.m[3][0] = 0.0f;
M.m[3][1] = 0.0f;
M.m[3][2] = -fRange * NearZ;
M.m[3][3] = 1.0f;
return M;

参考文献

https://zhuanlan.zhihu.com/p/473031788
https://blog.csdn.net/qq_31910239/article/details/118583533
https://blog.csdn.net/qq_20828983/article/details/82382573