文章目录
- 前言
- 一、OFDM 总体概述
- 1、OFDM 概述
- 2、OFDM 优点
- 二、OFDM 基本原理
- 1、基本思想
- 2、OFDM 调制和解调
- 3、OFDM 系统的发射机和接收机框图
- 三、OFDM 系统数学模型
- 1、sinc 函数
- 2、OFDM 时域表达式
- 3、OFDM 频域表达式
- 四、OFDM 时域及频域仿真
- 1、绘制时域及频域波形
- ①、MATLAB 源码
- ②、仿真结果分析
- 2、优化 OFDM 频谱图第一版本
- ①、MATLAB 核心源码
- ②、仿真结果分析
- 3、优化 OFDM 频谱图第二版本
- ①、MATLAB 核心源码
- ②、仿真结果分析
- 五、资源自取
- 总结
前言
本文讲解了 OFDM 相关概念及原理,并通过 MATLAB 仿真模拟一个 OFDM 时域及频域波形图。
一、OFDM 总体概述
1、OFDM 概述
OFDM(Orthogonal Frequency Division Multiplexing)即正交频分复用技术,是一种特殊的多载波传输方案,它可以被看作是一种调制技术,也可以被当作一种复用技术。简而言之就是用多个相互正交的子载波搭载信息进行传输。
下面对正交频分复用字面意思进行理解:
- 正交:可区分
- 频分:多个载波
- 复用:频率可重复使用
为了形象的理解,下面以 OFDM 频谱图进行讲解
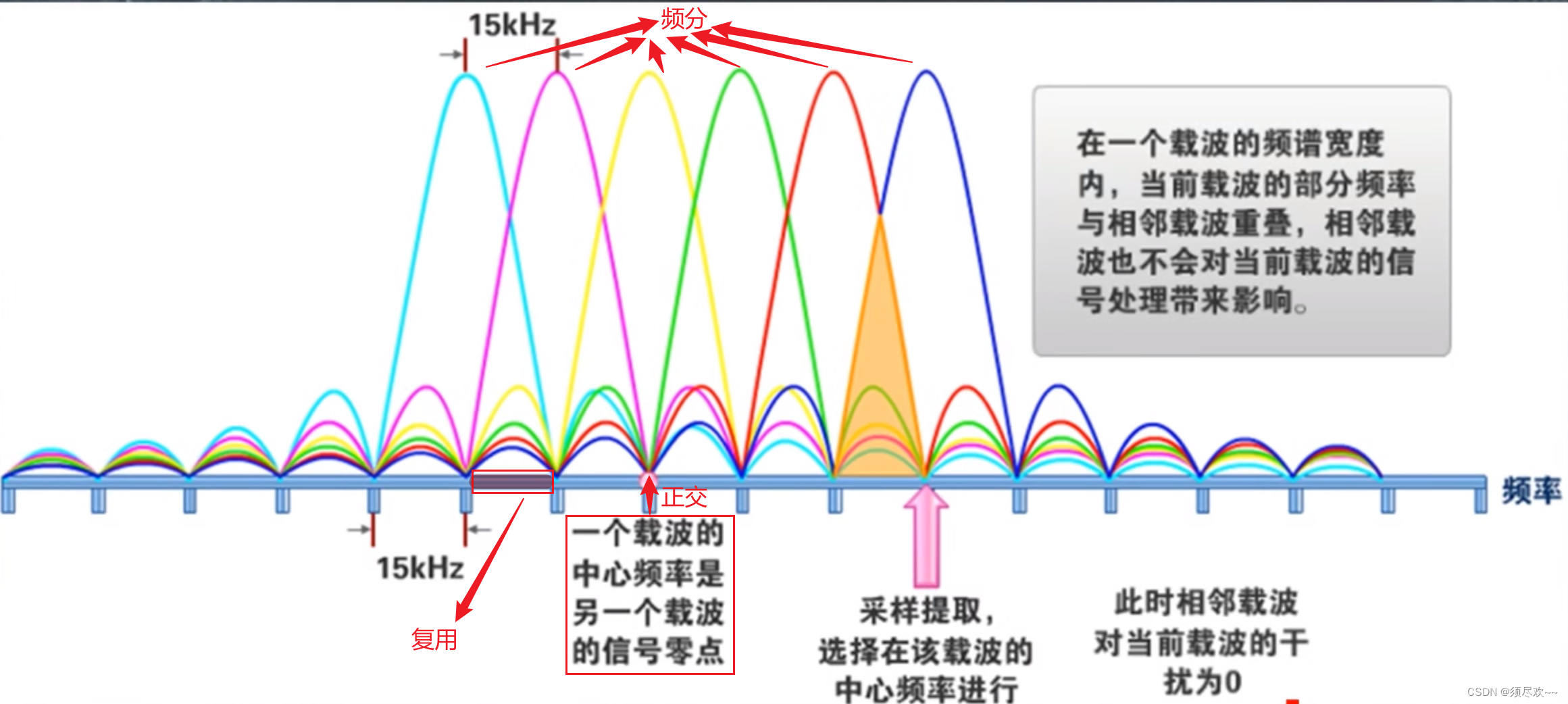
图中每一种颜色的“小山包”都是代表一个子载波,图中有 6 个子载波
①、那么如何体现出的正交呢?也就是上面提出的可区分
答:其中一个子载波的中心频率是其他子载波的信号的零点,也就是说在每一个子载波中心频率处,当前子载波的具有巨大的信号强度,可以检测到最大的能量,其他子载波信号强度都为 0,检测到的能量为 0,如此达到了可区分的目的,即为正交。
②、如何体现出了频分呢?也就是上面说的多个载波
答:图中不仅一个子载波,具有 6 个子载波,每个子载波的中心频率不同,达到了一个频分的目的,即为频分
③、如何体现出了复用呢?也就是上面说的频率可重复使用
答:从图中前两个子载波可以看到它们在频率上有重叠的部分,也就是达到了频率可重复使用的目的,即为复用
2、OFDM 优点
早期发展的无线网络或移动通信系统,是使用单载波调制(Single-carrier Modulation)技术,单载波调制是将要传送的信号(语音或数据),隐藏在一个载波上,再藉由天线传送出去。信号若是隐藏于载波的振幅,则有 AM、ASK 调制系统;信号若是隐藏于载波的频率,则有 FM、FSK 调制系统;信号若是隐藏于载波的相位,则有 PM、PSK 调制系统。
使用单载波调制技术的通讯系统,若要增加传输的速率,所须使用载波的带宽必须更大,即传输的符元时间长度(Symbol Duration)越短,而符元时间的长短会影响抵抗通道延迟的能力。若载波使用较大的带宽传输时,相对的符元时间较短,这样的通讯系统只要受到一点干扰或是噪声较大时,就可能会有较大的误码率(Bit Error Ratio,BER)。
为降低解决以上的问题,因此发展出多载波调制(Multi-carrier Modulation)技术,其概念是将一个较大的带宽切割成一些较小的子通道(Subchannel)来传送信号,即是使用多个子载波(Subcarrier)传来送信号,利用这些较窄的子通道传送时,会使子通道内的每一个子载波的信道频率响应看似平坦,这就是分频多任务(Frequency Division Multiplexing,FDM)观念。
因为带宽是一个有限的资源,若频谱上载波可以重迭使用,那就可以提高频谱效率(Spectrum Efficiency,η),所以有学者提出正交分频多任务(Orthogonal Frequency Division Multiplexing,OFDM)的技术架构。FDM 与 OFDM两者最大的差异,在OFDM 系统架构中每个子信道上的子载波频率是互相正交,所以频谱上虽然重迭,但每个子载波却不受其他的子载波影响。
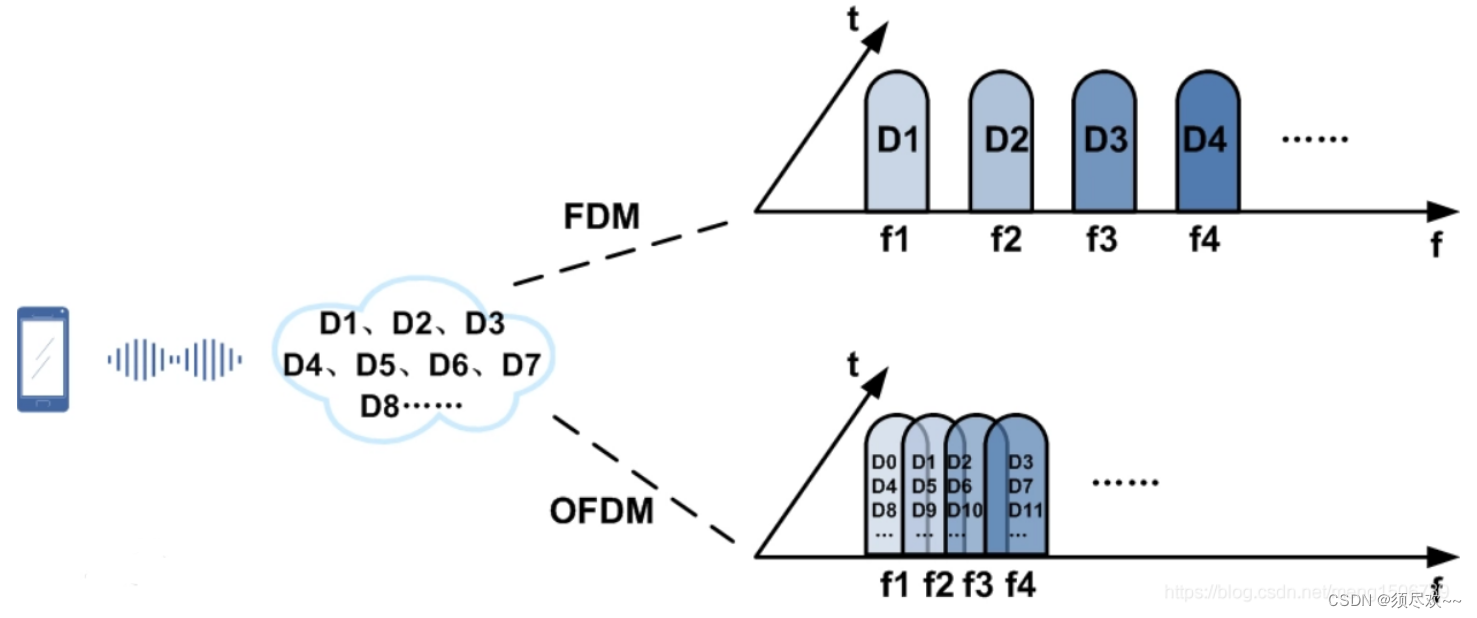
如上图所示,OFDM 所须的总带宽较小,倘若可以提供的载波总带宽是固定的,则 OFDM 系统架构将可以使用更多的子载波,使得频谱利用效率增加,提高传输量,而能应付高传输量需求的通讯应用。
上面没看明白如何提高了频带利用率?那就继续往下看,这些形象的图一定能让你看明白!!!
常规 FDM,两路信号频谱之间有间隔,互相不干扰,如下图所示
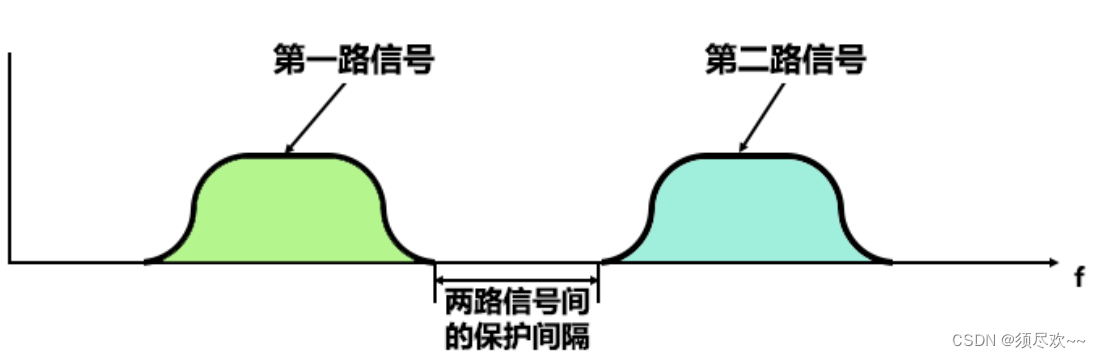
为了更好的利用系统带宽,子载波的间距可以尽量靠近些。如下图所示
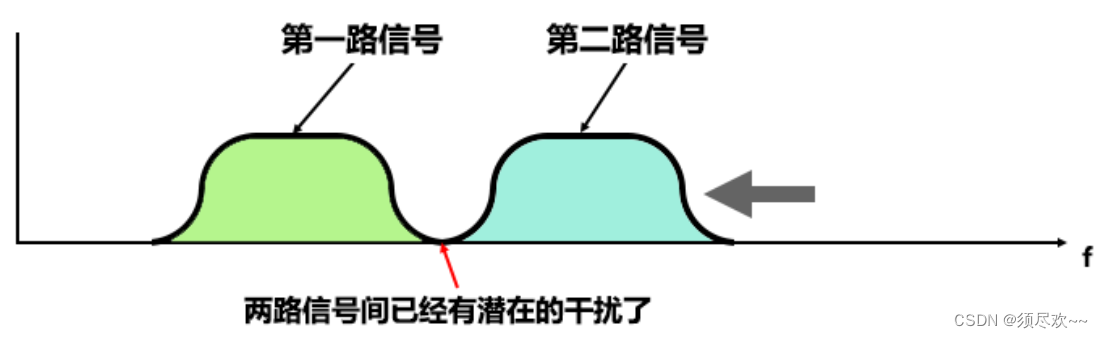
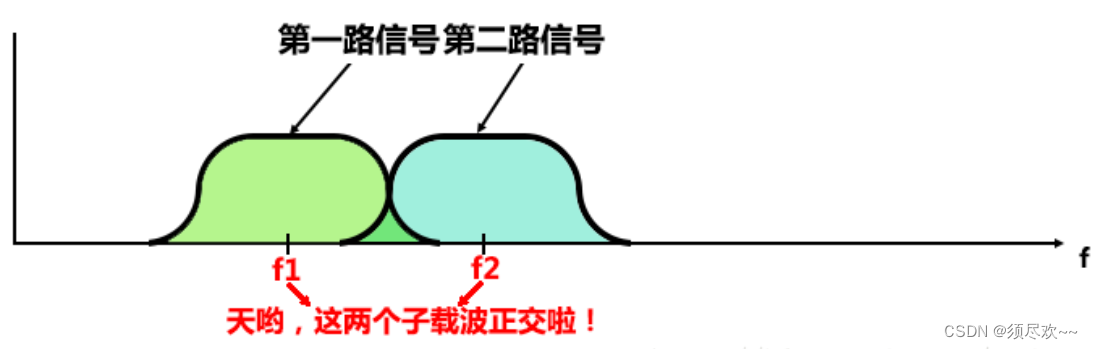
继续靠近,近到完全等同于奈奎斯特带宽(后面有详述),使频带的利用率达到了理论上的最大值
二、OFDM 基本原理
1、基本思想
OFDM 它的基本思想是在频域内将所给信道分成许多子信道,各个子信道之间保持正交。高速的数据流被分配到多个正交的子信道上进行传输,从而使子信道上的符号速率大幅度降低,单个数据符号的持续时间大大加长,因而具备了较强的抗时延扩展能力,降低了由于高速传输容易引起的符号间干扰(ISI)的影响。通常在 OFDM 符号送入信道前加保护间隔,只要保护间隔大于信道的最大时延扩展,那么理论上就可以完全消除 ISI 的影响,而通常的做法是加入循环前缀(CP),在有的系统中还加入循环后缀(CS),这是 OFDM 系统比较有特色的处理技术,在正交频分复用(OFDM)是多载波调制(MCM)技术的一种。
多载波调制的基本思想是把数据流串并变换为 N 路速率较低的子数据流,用这些子数据流分别去调制 N 路子载波以后,再并行传输。由于子数据流的速率是原来速率的 1/N,也就是说,符号周期扩大为原来的 N 倍,远大于信道的最大延迟扩展,这样,多载波调制就把一个宽带频率选择性信道划分成了 N 个窄带平坦衰落信道,这样均衡比较简单,从而具有很强的抗多径衰落以及抗脉冲干扰的能力,这样特别适合于高速无线数据传输。OFDM 是一种子载波相互混叠的多载波调制,因此它除了具有上述多载波调制的优势外,还具有更高的频谱利用率。OFDM 选择时域相互正交的子载波,它们虽然在频域互相混叠,却仍能在接收端被分离出来。
2、OFDM 调制和解调
OFDM 发射机将信息比特流映射成一个 PSK 或 QAM 符号序列,之后将符号序列转换成 N 个并行符号流,每 N 个经过串/并转换的符号被不同的子载波调制。
频域信号 X [ k ] X[k] X[k] 调制频率为 f k = k / T s y m f_k=k/T_{sym} fk=k/Tsym 的子载波,其中载波数量为 N = 6 N=6 N=6,即 k = 0 , 1 , 2 , . . . , 5 k=0,1,2,...,5 k=0,1,2,...,5。在接收机,利用子载波的正交性,可以解调这些信号。注意,原来符号 X [ k ] X[k] X[k] 的周期为 T s T_s Ts,由于串/并转换,通过并行发射 N N N 个符号, N N N 个符号的传输时间扩展为 N T s NT_s NTs,它是单个 OFDM 符号的持续时间 T s y m T_{sym} Tsym,即 T s y m = N T s T_{sym}=NT_s Tsym=NTs。OFDM 符号是 N 个并行符号的复合信号,其周期为 $T_{sym}。
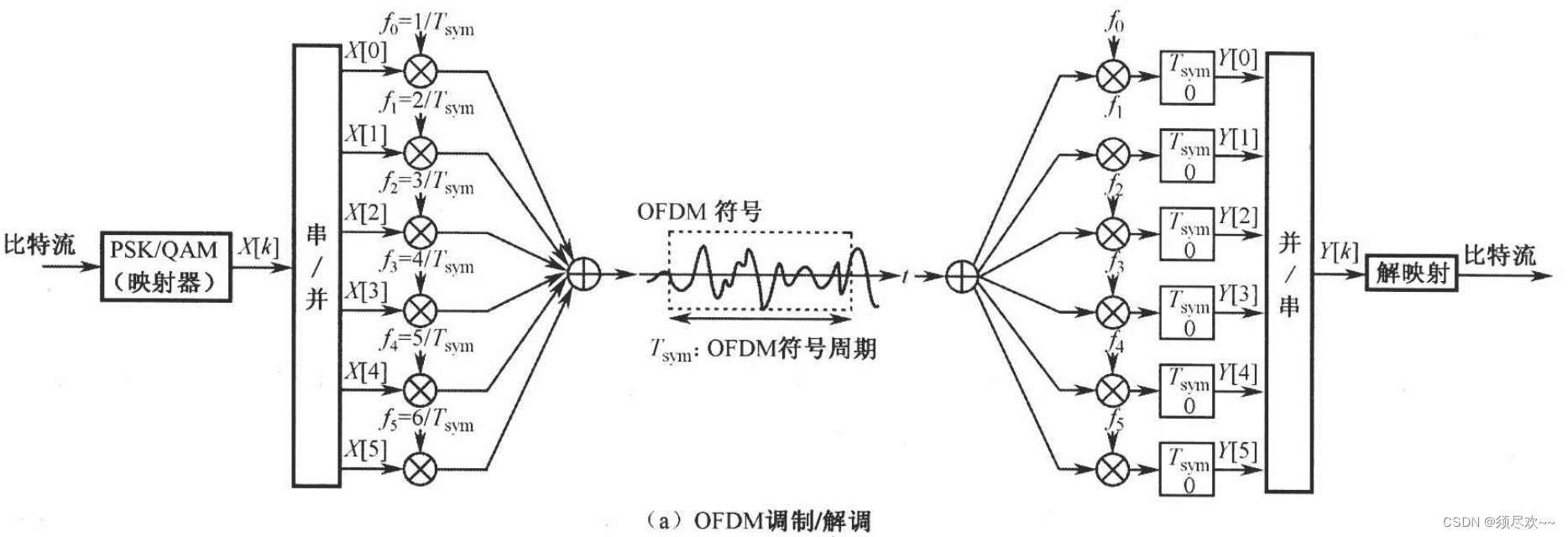
如下图所示,显示了所有子载波间正交性的一种典型实现。在发射机和接收机分别使用 IDFT、IFFT 和 DFT、FFT,可以实现这种多载波调制和解调。
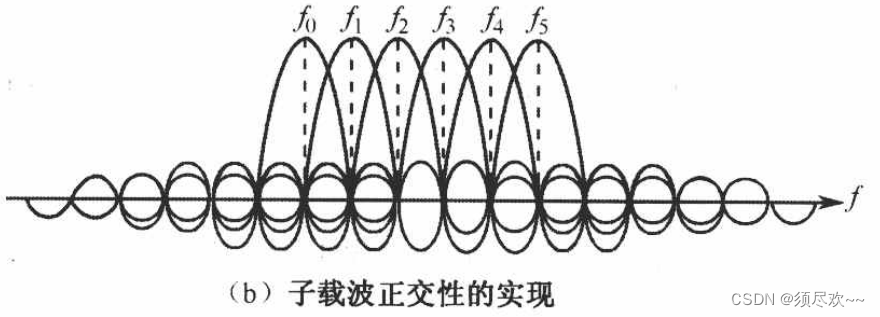
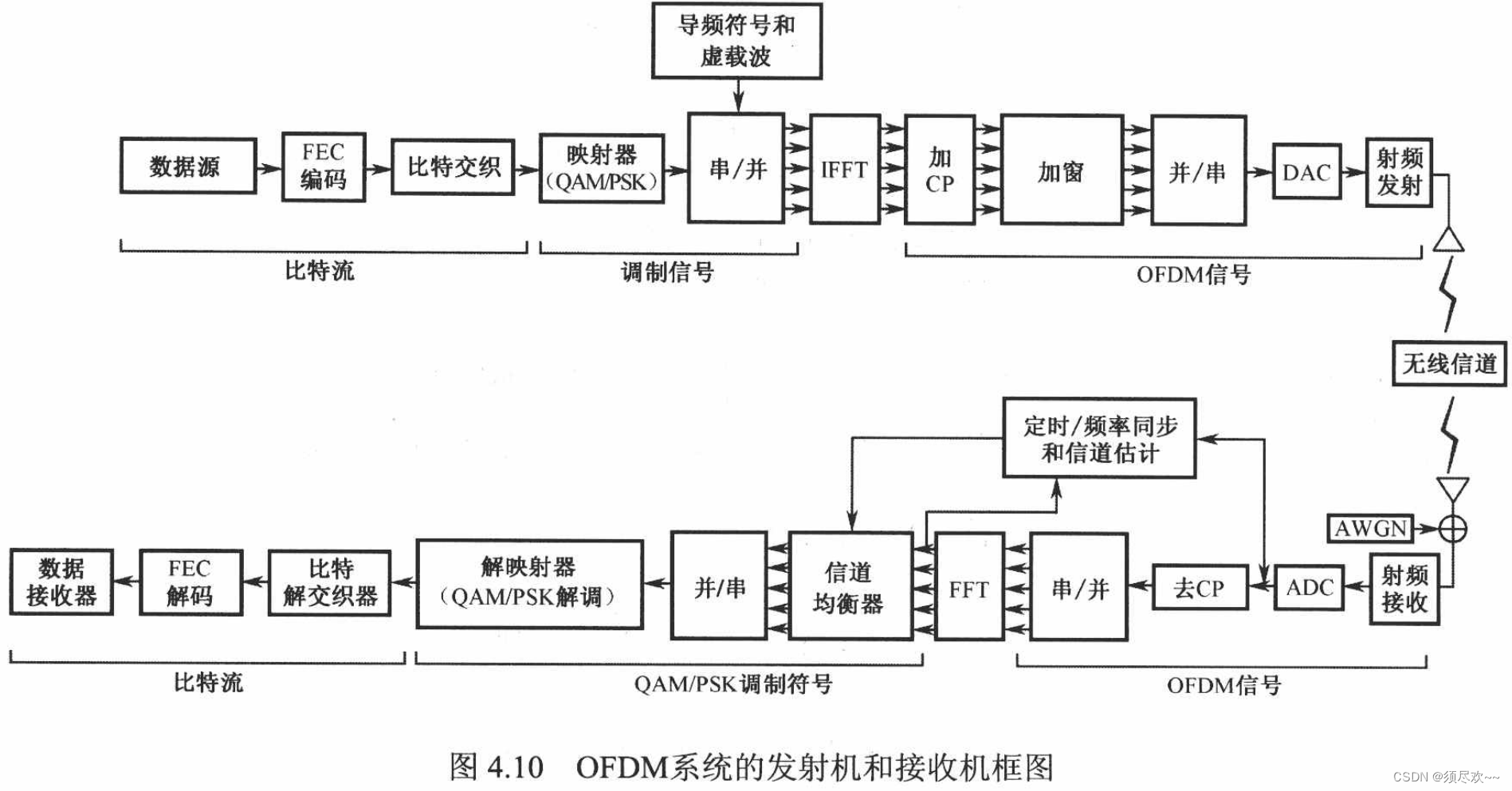
3、OFDM 系统的发射机和接收机框图
OFDM 系统的发射机和接收机框图如下图所示,这里的相关概念就不详细讲解了,如有感兴趣的读者可以阅读《MIMO-OFDM 无线通信技术及 MATLAB 实现》这本书籍,书里面有对相关概念进行了详细的讲解。
三、OFDM 系统数学模型
1、sinc 函数
问:常见于各种教材、论文的 OFDM 频谱图一般是多个 sinc 函数的叠加,那么为什么是 sinc 函数?
答:因为实际 OFDM 信号不可能是无限长的,而有限长的 OFDM 信号实际可以看做与矩形窗函数的乘积
矩形窗函数可以定义如下:
g
(
t
)
=
{
1
,
0
≤
∣
t
∣
≤
T
0
,
∣
t
∣
≥
T
g(t)= \begin{cases} 1,0\leq|t|\leq T \\ 0,|t|\geq T \\ \end{cases}
g(t)={1,0≤∣t∣≤T0,∣t∣≥T
对其进行傅里叶变换:
G
(
j
ω
)
=
∫
−
∞
∞
g
(
t
)
e
−
j
w
t
d
t
=
s
i
n
(
ω
T
/
2
)
ω
/
2
G(j\omega)=\int_{-\infty}^{\infty} {g(t)e^{-jwt}} \,{\rm d}t=\frac{sin(\omega T/2)}{\omega/2}
G(jω)=∫−∞∞g(t)e−jwtdt=ω/2sin(ωT/2)
由于时域相乘等效于频域卷积,因此 OFDM 信号反映到频谱,就成为各个不同位置的冲击响应与 sinc 函数的卷积。
对于 OFDM信号,形象点说在时域上是信号的叠加,在频域上是多个子载波并列。
OFDM(正交频分复用)信号的时域表达式可以表示为多个子载波的叠加。假设有 N 个子载波,每个子载波的频域符号为 X [ k ] X[k] X[k],其中 k k k 表示子载波的索引(从 0 到 N-1)。
2、OFDM 时域表达式
每个子载波的频域符号经过反快速傅里叶变换(IFFT)得到时域符号
x
[
n
]
x[n]
x[n],其中 n 表示时域的离散时间点(从 0 到 N-1)。那么 OFDM 信号的时域表达式可以表示为:
x
[
n
]
=
∑
k
=
0
N
−
1
X
[
k
]
⋅
e
j
2
π
n
k
/
N
x[n] = \sum_{k=0}^{N-1} X[k] \cdot e^{j2\pi nk/N}
x[n]=k=0∑N−1X[k]⋅ej2πnk/N
3、OFDM 频域表达式
每个子载波的频域符号经过快速傅里叶变换(FFT)得到频域符号
X
[
k
]
X[k]
X[k],其中 k 表示子载波的索引(从 0 到 N-1)。那么 OFDM 信号的频域表达式可以表示为:
X
[
k
]
=
1
N
∑
n
=
0
N
−
1
x
[
n
]
⋅
e
−
j
2
π
n
k
/
N
X[k] = \frac{1}{N} \sum_{n=0}^{N-1} x[n] \cdot e^{-j2\pi nk/N}
X[k]=N1n=0∑N−1x[n]⋅e−j2πnk/N
四、OFDM 时域及频域仿真
1、绘制时域及频域波形
①、MATLAB 源码
% ======================== 绘制时域波形图=======================
Fs = 1000; % 总的采样率
N = 1024; % 总的子载波数
T = N / Fs; % 信号绘制为一个周期的长度
x = 0 : 1/Fs : T-1/Fs; % 生成时间向量,用于绘制波形
Numscr = 4; % 绘制的子载波数量
s_data = 1; % 初始相位
y = zeros(Numscr, numel(x)); % 初始化存储每个子载波的复数值的矩阵
ini_phase = repmat(s_data, 1, numel(x)); % 生成与时间长度相匹配的初始相位向量
for k = 0 : Numscr-1 % 循环遍历要绘制的子载波数量
for n = 0 : numel(x)-1 % 循环遍历时间序列
y(k+1, n+1) = ini_phase(n+1) * exp(1i * 2 * pi * k * n / N); % 计算每个时间点上每个子载波的复数值
end
end
figure(1);
plot(x, real(y)); % 绘制时域波形
xlabel('时间/s'); % 设置 X 轴标签为“时间”
ylabel('幅度/V'); % 设置 Y 轴标签为“幅度”
% ======================== 绘制频域波形图=======================
f = (-Fs/2 : Fs/numel(x) : Fs/2-Fs/numel(x));
y_fft = zeros(Numscr, numel(x));
for k = 1 : Numscr
y_fft(k, :) = abs(fftshift(fft(y(k,:)))) / N; % 计算每个子载波的频谱
end
figure(2)
plot(f, y_fft(1,:), f, y_fft(2,:), f, y_fft(3,:), f, y_fft(4,:));
grid on;
xlim([-10, 10]); % 将 x 轴范围限制在 -10 到 10 之间
xlabel('频率/Hz');
ylabel('幅度/V');
②、仿真结果分析
OFDM 时域波形图如下:

可以验证上面的那句话:“对于 OFDM信号,形象点说在时域上是信号的叠加”。目前的图形是子载波分别绘制出来的结果,还未相加。
OFDM 频谱图如下:
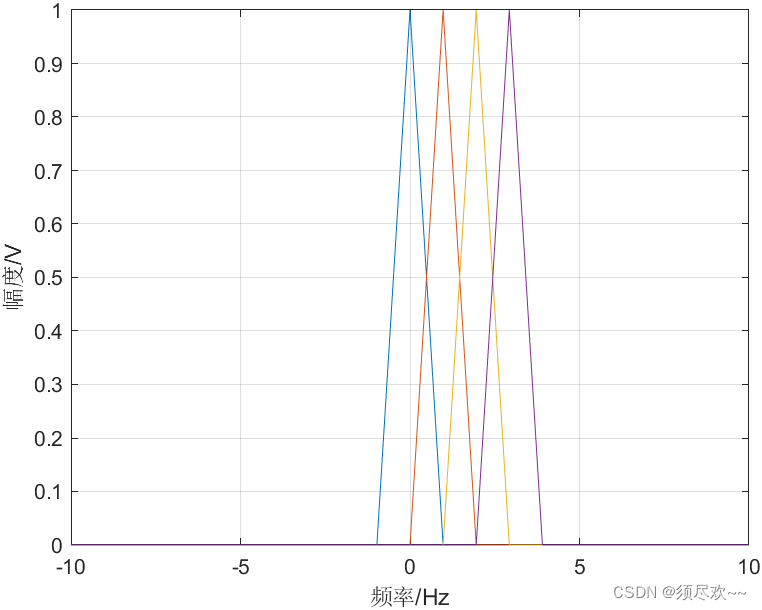
与理想的 sinc 波形相比甚远,这样肯定不行。若在时域进行补零,如下。
2、优化 OFDM 频谱图第一版本
①、MATLAB 核心源码
补 1024 * 20 个 0:
a = 20;
y1 = zeros(Numscr, a * N);
y_combined = horzcat(y, y1); % 水平拼接两个矩阵
f = (-Fs/2 : Fs/((a+1)*N) : (Fs/2-Fs/((a+1)*N)));
y_fft = zeros(Numscr, (a+1)*N);
for k = 1 : Numscr
y_fft(k, :) = abs(fftshift(fft(y_combined(k,:)))) / N; % 计算每个子载波的频谱
end
②、仿真结果分析
优化后的 OFDM 频谱图如下:
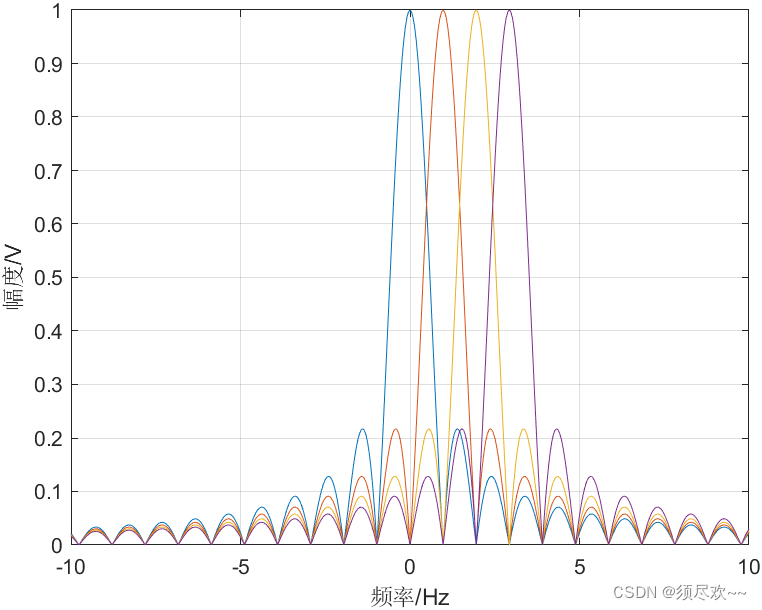
原因分析:时域尾部补零等效于频域插值,让频谱图形变得圆滑。
虽然图形比较理想,但频谱图小于等于 0 的部分我们没有看到:我们绘制的频谱图幅值都是大于等于 0 的。当然必然是大于等于 0 的,因为我们是取模进行绘制,也是正确的,但是怎么获得这种图:

3、优化 OFDM 频谱图第二版本
要绘制上图的图形,取模肯定是不行的,我们可以尝试取实部
①、MATLAB 核心源码
a = 20;
y1 = zeros(Numscr, a * N);
y_combined = horzcat(y, y1); % 水平拼接两个矩阵
f = (-Fs/2 : Fs/((a+1)*N) : (Fs/2-Fs/((a+1)*N)));
y_fft = zeros(Numscr, (a+1)*N);
for k = 1 : Numscr
y_fft(k, :) = real(fftshift(fft(y_combined(k,:)))) / N; % 计算每个子载波的频谱
end
②、仿真结果分析
优化后的 OFDM 频谱图如下:
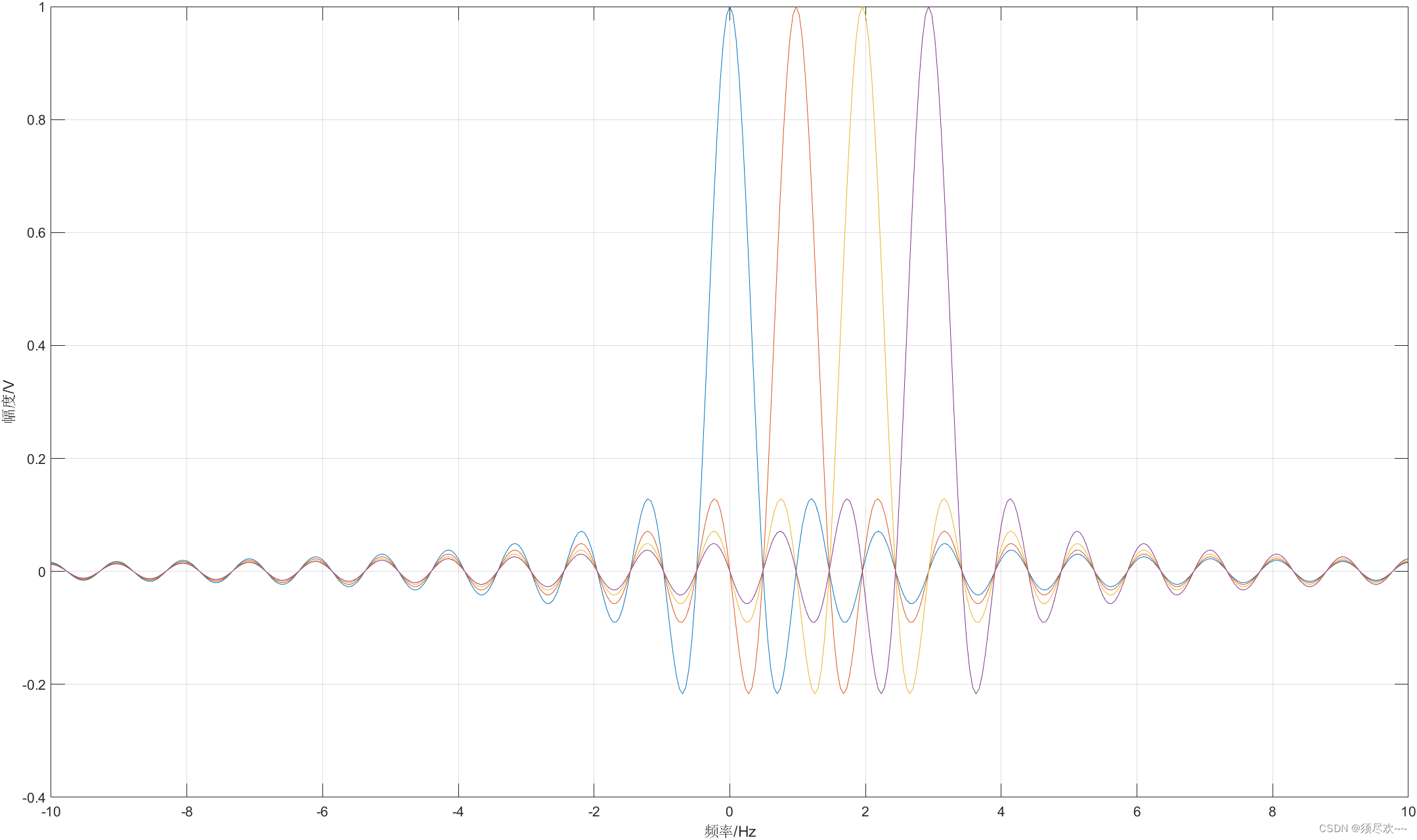
如此,获得了比较接近的频谱图。
五、资源自取
OFDM 时域及频域 MATLAB 仿真
总结
- 本文首先在 OFDM 总体概述部分对 OFDM 的基本概念进行了介绍,并强调了使用 OFDM 的优点是什么;
- 其次对 OFDM 的原理进行了基本的介绍,其中包括 OFDM的基本思想、OFDM 调制解调思想、OFDM系统的发射机和接收机组成框图;
- 然后对 OFDM 的数学模型进行了分析,包括时域及频域;
- 最后对 OFDM的时域及频域波形进行了 MATLAB 仿真,针对仿真过程中遇到的问题也进行了分析及解决。
我的qq:2442391036,欢迎交流!