(滑动窗口) 76. 最小覆盖子串 ——【Leetcode每日一题】

news2024/7/4 4:43:04

❓76. 最小覆盖子串

难度：困难

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。

注意：

对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
如果 s 中存在这样的子串，我们保证它是唯一的答案。

示例 1：

输入：s = “ADOBECODEBANC”, t = “ABC”
输出：“BANC”
解释：最小覆盖子串 “BANC” 包含来自字符串 t 的 ‘A’、‘B’ 和 ‘C’。

示例 2：

输入：s = “a”, t = “a”
输出：“a”
解释：整个字符串 s 是最小覆盖子串。

示例 3:

输入: s = “a”, t = “aa”
输出: “”
解释: t 中两个字符 ‘a’ 均应包含在 s 的子串中，
因此没有符合条件的子字符串，返回空字符串。

提示：

m == s.length
n == t.length
$1 <= m, n <= 10^5$
s 和 t 由英文字母组成

进阶：你能设计一个在 $O (m + n)$ 时间内解决此问题的算法吗？

💡思路：滑动窗口

滑动窗口的思想：
用 l 和 r 表示滑动窗口的左边界和 右边界，通过改变 l, r 来扩展和收缩滑动窗口，可以想象成一个窗口在字符串上游走，当这个窗口包含的元素满足条件，即包含字符串 t 的所有元素，记录下这个滑动窗口的长度 r - l +1，这些长度中的最小值就是要求的结果。

由于 t 可能包含 重复字符 ，所以使用哈希表 ori 记录 t 中所有的字符以及它们的个数；使用另一个哈希表 cnt 动态维护窗口中所有的字符以及它们的个数。

如果 当前窗口 中包含 t 中所有的字符，且对应的字符个数都不小于 t 的哈希表中各个字符的个数，则当前窗口是「可行」的。此时左边界 l 右移，直到不涵盖 t 中的所有字符，上一个即为满足条件的 当前窗口的最小子串。

使用 distance 记录 当前窗口 中字符属于 t 对应的个数；当 cnt[s[r]] < ori[s[r]] 时，每增加一个 s[r]， distance ++ ，否则 distance 不变。同理当 cnt[s[l]] <= ori[s[l]] 每减少一个 s[l]， distance -- ，否则 distance 不变。（这样可以在 $O (1)$ 的复杂度判断当前窗口内的字符是否符合要求）

具体步骤如下：

不断增加 r 使滑动窗口增大，直到窗口包含了 t 的所有元素；
不断增加 l 使滑动窗口缩小，因为是要求最小字串，所以将不必要的元素排除在外，使长度减小，直到碰到一个必须包含的元素，这个时候不能再扔了，再扔就不满足条件了，记录此时滑动窗口的长度，并保存最小值；
让 l 再增加一个位置，这个时候滑动窗口肯定不满足条件了，那么继续从 步骤 1 开始执行，寻找新的满足条件的滑动窗口，如此反复，直到 r 超出了字符串 s 范围。

🍁代码：(C++、Java)

C++

class Solution {
public:
    unordered_map <char, int> ori, cnt;

    string minWindow(string s, string t) {
        for(const auto &c : t){ //使用哈希表记录t中所有的字符，及其对应的个数
            ++ori[c];
        }
        int l = 0, r = -1;
        int len = INT_MAX, ansl = -1;
        int distance = 0;

        while(r < int(s.size())){
            if(ori.find(s[++r]) != ori.end() && ++cnt[s[r]] <= ori[s[r]] ){//对任何属于t的字符都记录
                distance++;//记录当前窗口的子串中属于t的字符的个数
            }
            while(distance == t.size() && l <= r){//包括所有字符，左指针右移
                if(r - l + 1 < len){//更新结果
                    len = r - l + 1;
                    ansl = l;
                }
                if(ori.find(s[l]) != ori.end() && --cnt[s[l]] < ori[s[l]]){
                    distance--;
                }
                ++l;
            }
        }
        return ansl == -1 ? string() : s.substr(ansl, len);
    }
};

Java

class Solution {
    Map<Character, Integer> ori = new HashMap<Character, Integer>();
    Map<Character, Integer> cnt = new HashMap<Character, Integer>();
    public String minWindow(String s, String t) {
        for(int i = 0; i < t.length(); i++){//使用哈希表记录t中所有的字符，及其对应的个数
            char c = t.charAt(i);
            ori.put(c, ori.getOrDefault(c, 0) + 1);
        }
        
        int l = 0, r = -1;
        int len = Integer.MAX_VALUE, ansl = -1;
        int distance = 0;
        while(++r < s.length()){
            char c = s.charAt(r);
            if(ori.containsKey(c)){//对任何属于t的字符都记录
                cnt.put(c, cnt.getOrDefault(c, 0) + 1);
                if(cnt.get(c) <= ori.get(c)){//记录当前窗口的子串中属于t的字符的个数
                    distance++;
                }
            }
            while(distance == t.length() && l <= r){
                if(r - l + 1 < len){//更新结果
                    len = r - l + 1;
                    ansl = l;
                }
                if(ori.containsKey(s.charAt(l))){
                    cnt.put(s.charAt(l), cnt.getOrDefault(s.charAt(l), 0) - 1);
                    if(cnt.get(s.charAt(l)) < ori.get(s.charAt(l))){
                        distance--;
                    }
                }
                ++l;
            }
        }
        return ansl == -1 ? "" : s.substring(ansl, ansl + len);
    }
}

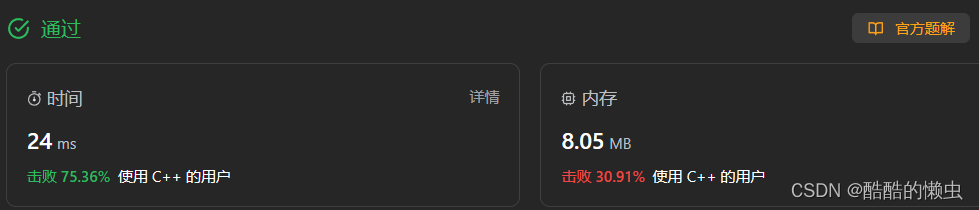
🚀 运行结果：

在这里插入图片描述

🕔 复杂度分析：

时间复杂度： $O (∣ s ∣ + ∣ t ∣)$ ，最坏情况下左右指针对 s 的每个元素各遍历一遍，哈希表中对 s 中的每个元素各插入、删除一次，对 t 中的元素各插入一次。
空间复杂度： $O (C)$ ，这里用了两张哈希表作为辅助空间，每张哈希表最多不会存放超过字符集大小的键值对，我们设字符集大小为 C ，则渐进空间复杂度为 $O (C)$ 。